Площадь треугольника

Каковы бы ни были три точки А(х₁; y₁), B(x₂; у₂) и С(x₃; у₃) площадь S треугольника ABC дается формулой

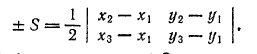
Правая часть этой формулы равна +S в том случае, когда кратчайший поворот отрезка АB к отрезку АC положителен, и -S в том случае, когда такой поворот отрицателен.

116. Вычислить площадь треугольника, вершинами которого являются точки: 1) А(2; -3), B(3; 2) и С(-2; 5); 2) М₁(-З; 2), М₂(5; -2) и М₃( 1; 3); 3) М(3; -4), N(-2; 3) и Р(4; 5).

117. Вершины треугольника суть точки A(3; 6), B( - 1; 3) и С(2; -1). Вычислить длину его высоты, проведенной из вершины С.

118. Определить площадь параллелограмма, три вершины которого суть точки А (-2; 3), 5(4; -5) и С(-3; 1).

119. Три вершины параллелограмма суть точки A(3; 7), B(2; -3) и С(- 1; 4). Вычислить длину его высоты, опущенной из вершины B на сторону АС.

120. Даны последовательные вершины однородной четырехугольной пластинки A(2; 1), B(5; 3), С(- 1; 7) и D(-7; 5). Определить координаты ее центра тяжести.

121. Даны последовательные вершины однородной пятиугольной пластинки A(2; 3), B(0; 6), С(-1; 5), D(0; 1) и E(1; 1). Определить координаты ее центра тяжести.

122. Площадь треугольника S = 3, две его вершины суть точки A(3; 1) и B(1; -3), а третья вершина С лежит на оси Оу. Определить координаты вершины С.

123. Площадь треугольника S = 4, две его вершины суть точки A(2; 1) и B(3; -2), а третья вершина С лежит на оси Ох. Определить координаты вершины С.

124. Площадь треугольника S = 3, две его вершины суть точки A(3; 1) и B(1; -3), центр тяжести этого треугольника лежит на оси Ох. Определить координаты третьей вершины С.

125. Площадь параллелограмма S = 12 кв. ед.; две его вершины суть точки А(-1; 3) и B(-2; 4). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси абсцисс.

126. Площадь параллелограмма S = 17 кв. ед.;- две его вершины суть точки A(2; 1) и B(5; -3). Найти две другие вершины этого параллелограмма при условии, что точка пересечения его диагоналей лежит на оси ординат.