Часть первая
Решение задач1. См. рис. 54. 2. Указание. Уравнение |х| = 2 эквивялентно двум уравнениям: х= - 2 и х = 2; соответственно имеем две точки: A1 (- 2) и 2 (2) (рис. 55). Уравнение |x - 1| = 3 экви-
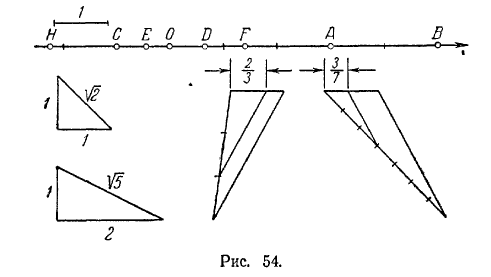
валентно двум уравнениям: х - 1 = -3 и х- 1=3, откуда находим x = -2 и х = 4 и соответствующие им точки B1 и В2 (рис. 55).В остальных случаях решения аналогичны. 3. Точки расположены: 1) справа от точки M1 (2); 2) слева от точки М2 (3); включая точку М2; 3) справа от точки М3 (12); 4) слева от точки М4(3/2) включая точку М4; 5) справа от точки М5(5/3); 6) внутри отрезка, ограниченного точками M6(1) и M2(3) ; 7) внутри отрезка, ограниченного точками М7(-2) и M2(3), включая точки М7 и M2; 8) внутри отрезка, ограниченного точками A(1) и В{2); 9) вне отрезка, ограниченного точками Р (- 1) и Q (2); 10) вне отрезка, ограниченного точками A(1) и В (2); 11) внутри отрезка, ограниченного точками Р(-1) и Q (2); 12) внутри отрезка, ограниченного точками M(3) и N(5), включая точки M и N; 13) вне отрезка, ограниченного точками M(3) и N(5) ; 14) вне отрезка, ограниченного точками P1(-4) и Q1(3); 15) внутри отрезка, ограниченного точками P1 (-4) и Q1 (3), включая точки P1 и Q1
4. 1) AB =8, |AB| = 8; 2) AB = -3, |AB| = 3; 3) AB = 4, |AB| = 4, 4) AB = 2, |AB| =2; 5) AB = -2, |AB| =2; 6) AB =2, |AB| = 2;
5. 1) -2; 2) 5; 3) 1; 4) -8; 5) -2 и 2; 6) -1 и 5; 7) -6 и 4; 8) -7 и -3.
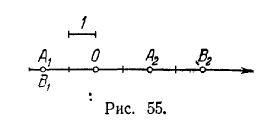
6. I) Внутри отрезка, ограниченного точками A(-1) и В (1)); 2) вне отрезка, ограниченного точками A (-2) и В (2); 3) внутри отрезка, ограниченного точками A (-2) и В (2), включая точки A и В; 4) вне отрезка, ограниченного точками A (-3) и В (3), включая точки A и В; 5) внутри отрезка, ограниченного точками A(-1) и В (5); 6) внутри отрезка, ограниченного точками A (4) и В (6), включая точки A и В; 7) вне отрезка, ограниченного точками A (-1) и В (3), включая точки A и В; 8) вне отрезка, ограниченного точками A (2) и В (4), включая точки A и В; 9) внутри отрезка, ограниченного точками A(-4) и В (2); 10) вне отрезка, ограниченного точками A(-3) и В( -1); 11) A и В; 12) вне отрезка, ограниченного точками A (-3) и В (1), включая точки A и B

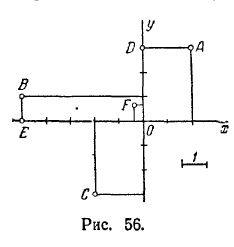
4) 7; 5) 3; 6) 0. 14. 1) M (-11); 2) N(13). 15) (5) и (12). 16. A(7) и B(-41); 17. См. рис. 56 18. Ax (2;0), Сx (-5; 0), Dx(-3; 0), Ex(-5; 0). 19. Ay (0; 2), Вy (0; 1), Сy(0; -2), Dy(0; 1), Еy(0; -2); 20. 1) (2; -3); 2) (-3; -2); 3) ( - 1; 1); 4) (-3;5); 5) (-4; -6); 6) (а;- b), 21. 1) (1; 2); 2) (-3; -1); 3) (2; -2); 4) (2; 5); 5) (-3; -5); 6) (-а; b). 22. 1) (-3; -3); 2) (-2; 4); 3) (2; -1); 4) (-5; 3); 5) (5; 4); 6) (- а; - b). 23. 1) (3; 2); 2) (-2; 5); 3) (4; -3). 24. 1)(-5; -3); 2) (-3; 4); 3) (2; -7).
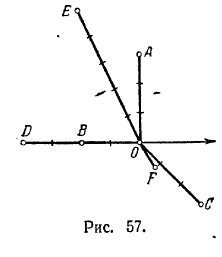
25. 1) В первой и третьей; 2) во второй и четвертой; 3) в первой и третьей; 4) во второй и четвертой; 5) в первой, второй и четвертой; 6) во второй, третьей и четвертой; 7) в первой, третьей и четвертой; 8) в первой, второй и третьей. 26. См. рис. 57
27. (3; -π/4), (2; π/2), (3;π/3), (1; -2), (5; 1). 28. (l; -3/4π), (5;-π/2),
(2; 2/3π), (4; -1/6π), (3; π-2). 29. C(3;5/9π) и D(5; -11/14π).
30. (l; -2π/3). 31. A(3; -π/2), B(2 ; 3/4π), С (1; 0), D (5; π/4), E (3; 2 - π), F (2; π - 1). 32. М1 (3; 0), М2 (l; π/3), М3 (2; - π/3), M4 (5; -π/12), М5(3;π), M6(l; 7/12π). 33. (6; π/9)
34. d = √(р21 + Р22 - 2р1р2 cos ( Θ2 - Θ1)). 35. d = 7. 36. 9 (17-4√3) кв. ед.
37. 2(13 + 6√2)кв. ед. 38.28√3 кв. ед. 39. S = 1/2 р1р2 [sin (Θ1 - Θ2)]. 40. 5 кв. ед.
41. 3(4√3- 1) кв. ед. 42. M1 (0; 6), M2(5; 0), М3(√2; √2), M4(5;-5√3), M5(-4; 4√3), M6(6√3; -6).
43. М1 (5; π/2), М2(3; π), M3 (2; π/6), M4 (2; -3/4π), М5(2;-1). 44 1)3; 2) -3; 3) 0; 4) 5; 5) -5; 6) 2.
47. 1) X = 1, У = 3; 2) X = - 4. У = - 2; 3) X = 1, У = - 7; 4) X = 5, У = 3.
48. (3; -1). 49. (-3; 2). 52. 1) X = - 6, У = 6√3; 2) X = 3√3, У = - 3; 3) X = √2, У = - √2. 53. 1) 5; 2) 13; 3) 10. 54. 1) d = 2, Θ = π/3; 2) d = 6, Θ = - π/4 ; 3) d = 4, Θ = 5/6π. 55. 1) d =√2, Θ = -3/4π; 2) d = 5, Θ = arctg4/3 - π; 3) d = 13, Θ = π - arctg12/5 ; 4) d = √234, Θ = - arctg 5. 56. 1) 3; 2) -3. 57. 1) (-9; 3); 2) (-9; -7).
58. 1) (-15; -12); 2) (1; -12). 59. -2. 60.(3√3 - 4)/2. 61. 4.
62. 1) -5; 2) 5. 63. 1) 5; 2) 10; 3) 5; 4) 4√5; 5) 2√2; 6) 13. 64 137 кв. ед. 65. 34 кв. ед. 66. 8√3 кв. ед. 67. 13,15. 68. 150 кв. ед.

78. М1 (0; 28) и М2 (0; -2). 79. Р1 (1; 0) и Р2 (6; 0). 80. С1 (2; 2), = 2; С2 (10; 10), R2 = 10. 81. С1 (-3; -5), С2(5; -5). 82. M2 (3; 0). 83. B(0; 4) и D(-1; -3). 84. Условию задачи удовлетворяют два квадрата, симметрично расположенных относительно стороны АВ. Вершины одного квадрата суть точки С1 (-5; 0), Dx1(- 2; -4), вершины другого - С2 (3; 6), D2(6;2). 85. С (3; - 2), R = 10.
86. (1; -2). 87. Q (4; 6). 88. Середины сторон АВ, ВС, АС соответственно суть (2;-4), (-1; 1), (-2; 2). 89. 1)M(1;3); 2)N(4;-3). 90. (1; -3), (3; 1) и (-5; 7). 91. D (-3; 1). 92. (5; -3), (1; -5).
93. D1(2;l), D2 (-2; 9), D3 (6; -3). Указание. Четвертая вершина параллелограмма может быть противоположной любой из данных. Таким образом, условию задачи удовлетворяют три параллелограмма.
94. 13. 95. (2; -1) и (3; 1). 96. (5/2; -2). 97. 14/3√2.
98. (-11; -3). 99. 4. 100. λ1 = AB?BC = 2; λ2 = AC?CB = -3; λ2 = BA/AC = -2/3. 101. A(3;-1) и В(0;8). 102.(3;-1). 103. (4;-5).
104. (-9;0). 105. (0; -3). 106. 1:3, считая от точки В. 107.(41/2; 1). 108. x = (x1 + x2 + x3)/3, y = (y1 + y2 + y3)/3 109. M (-1; 0); С(0;2).
111. (5; 5). 112.(5/12a; 5/12b). 113. (19/21a; 19/21a).
114. x = (mx1 + mx2 + mx3)/(m + n + p), y = (my1 + myy2 + my3)/(m + n + p) . 115. (4 ; 2)
Указание. Вес однородной проволоки пропорционален ее длине.
116. 1) 14 кв, ед.; 2) 12 кв. ед.; 3) 25 кв. ед. 117. 5. 118. 20 кв. ед.
119. 7,4. 120. х = -6/11, y = 4 1/11. 121. x = 7/17, y = 3 1/3.
122. (0; -8) или (0; -2). 123. (5; 0) или (-1/3; о). 124. (5; 2) или (2; 2). 125. С1 (-7; -3), D1 (-6; -4) или С2(17; -3), D2(18; -4). 126. C1(-2; 12), D1 (-5; 16) или С2(-2;2/3),
D2(-5;14/3). 127. I) x = x' + 3, у = у' + 4; 2) х = х' - 2, у = у'+ 1; 3) x = x' - 3, у = у' + 5. 128. A (4; -1), В (0; -4), С (2; 0). 129. 1) A (0; 0), В (-3; 2), С (-4; 4); 2) A (3; -2), В (0; 0), С (-1; 2); 3) A (4; -4), В (1; -2), С (0; 0).130. 1) (3; 5); 2) (-2; 1); 3) (0; -1); 4) (-5; 0). 131. 1) x = (x' - y'√3)/2, y = (x'√3 - y')/2 . 2) х = (x' + y')/√2 , y = (-x' + y')/√2 3) x = -y', y = х'; 4) х = у', 5) y = -x', у = -у'. 132. A(3√3; 1), B(√3/2;3/2), С( 3; -√3).
133. 1) М(√2; 2√2), N(-3√2; 2√2 ), N( -3√2 ; 2√2); 2) M(l; -3), N(5; 1), P(-l; 3); 3) М(-1; 3), N (-5; -1), Р (1; -3); 4) М (-3; -1), N (1; -5), Р (3; 1). 134. 1) 60°; 2) -30°. 135. О'(2; -4). 136.. x = x' + 1, y = у' - 3.
137. x = 3/5x' + 4/5y', y = -4/5x' + 3/5y'; 138. M1 (1; 5), М2 (2; 0), М3 (16; -5). 139. A (6; 3), В (0; 0), С (5; -10). 140. 1) О' (3; -2), α = 90°; 2) O'(-1; 3), α =180°; 3) О'(5; -3), α = -45°.
141. х = -15/17х'- 8/17у' + 9, у = 8/17х'- 15/17у' - 3. 142. М1(1: 9),
М2 (4; 2), М3 (1; -3), М4 (0; 2 + √3), М5 (l + √3; l). 143. М1 (0; 5), М2(3;.0), М3(-1; 0), М4 (0; -6), М5(√3;1). 144. М1 (2; 0), М2(1;-π/2),М3(3;π/2), 145. M1 (√2; 1/2π), M2(2; -π/2), M3(2; π/2), M4(2; 7/12π), M1 (4; -5/12π).
146. f(x, y) = 2ax - a2. 147. 1) f(x,y) = 2ax; 2) f (x, y) = -2ax - a2. 148. f (x, y) = 4x2 + 4y2 + 2a2.
149. f (x, y) = 4x2 + 4у2 - 4ax - 4аy + 4а2. 150. f {х, у) = х2 + у2 - 25. 151. f (х, у) = 2xy - 16.
152. При повороте координатных осей выражение функции не меняется. 153. (3; 1). 154. Такой точки не существует. 155. ±45° или ± 135°. 156. 30°, 120°, -60°, - 150°. 157. Точки М1 М4 и М5 лежат на линии; точки М2, М3 и М6 не лежат на ней. Уравнение определяет биссектрису второго и четвертого координатных углов
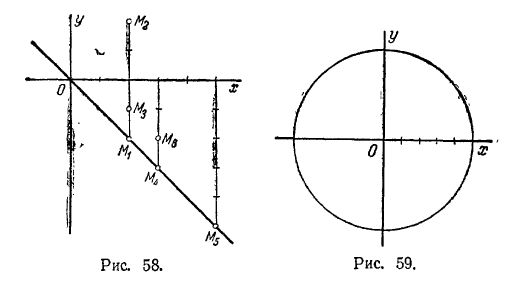
(рис. 58). 158. 1) (0; -5), (0; 5); 2) (-3; -4), (-3; 4); 3) (5; 0); 4) на данной линии такой точки нет; 5) (-4; 3), (4; 3); 6) (0; -5);
7) на данной линии такой точки нет. Уравнение определяет окружность с центром O(0; 0) и радиусом 5 (рис. 59). 159. 1) Биссектриса первого и третьего координатных углов;
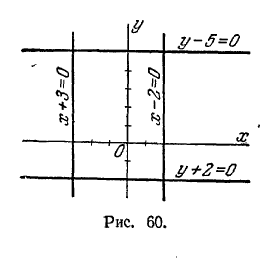
2) биссектриса второго и четвертого координатных углов; 3) прямая, параллельная оси Оу, отсекающая на положительной полуоси Ох, считая от начала координат, отрезок, равный 2 (рис. 60); 4) прямая, параллельная оси Оу, отсекающая на отрицательной полуоси Ох, считая от начала координат, отрезок, равный 3 (рис. 60); 5) прямая, парал-лельная оси Ох, отсекающая на положительной полуоси Оу, считая от начала координат, отрезок, равный 5 (рис. 60); 6) прямая, параллельная оси Ох, отсекающая на отрицательной полуоси Оу, считая от начала координат, отрезок, равный 2 (рис. 60); 7) прямая, совпадающая с осью ординат; 8) прямая, совпадающая с осью абсцисс; 9) линия состоит из двух прямых: биссектрисы первого и третьего координатных углов и прямой, совпадающей с осью ординат; 10) линия состоит из двух прямых: биссектрисы второго и четвертого координатных углов и прямой, совпадающей с осью абсцисс; 11) линия состоит из двух биссектрис координатных углов (рис. 61); 12) линия состоит из двух прямых: прямой, совпадающей
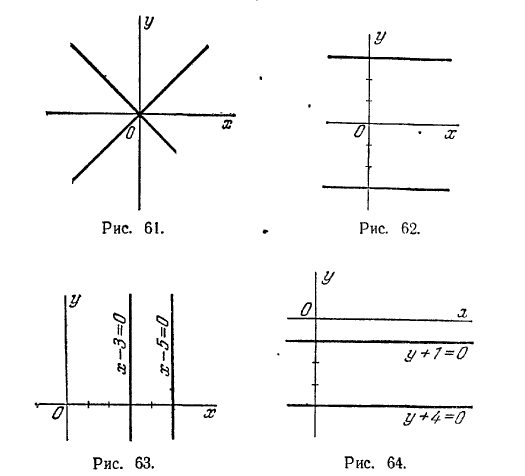
с осью абсцисс, и прямой, совпадающей с осью ординат; 13) линия состоит из двух прямых, параллельных оси абсцисс, которые отсекают на оси ординат, считая от начала координат, отрезки, равные 3 и - 3 (рис. 62); 14) линия состоит иэ двух прямых, параллельных оси щОу, которые ютсекают на положительной полуоси Ох, считая от начала координат, отрезки, равные 3 и 5 (рис. 63); 15) линия состоит из двух прямых, параллельных оси Ох, которые отсекают на отрицательной полуоси Оу, считая от начала координат, отрезки, равные 1 и 4 (рис. 64); 16) линия состоит из трех прямых: прямой, совпадающей с осью абсцисс, и двух прямых, параллельных оси ординат, которые отсекают на положительной полуоси абсцисс, считая от начала координат, отрезки, равные 2 и 5; 17) линия состоит из двух лучей: биссектрис первого и второго координатных углов (рис. 65); 18) линия состоит из двух лучей: биссектрис
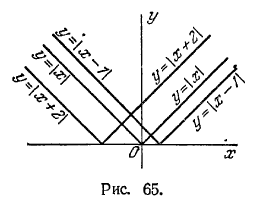
первого и четвертого координатных углов (рис. 66, а); 19) линия со стоит из двух лучей: биссектрис третьего и четвертого координатных углов (рис. 66, б); 20) линия состоит из двух лучей: биссектрис второго и третьего координатных углов (рис. 66, в);
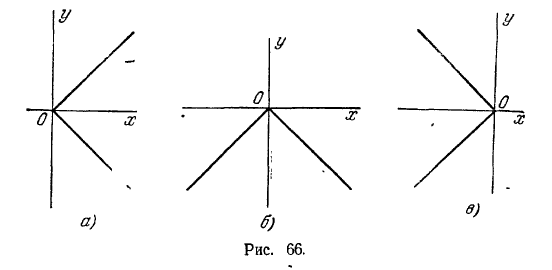
21) линия состоит из двух лучей, расположенных в верхней полуплоскости, выходящих из точки (1; 0) и направленных параллельно биссектрисам координатных углов (рис. 65); 22) линия состоит из двух лучей, расположенных в верхней полуплоскости, выходящих из точки (-2; 0) и направленных параллельно биссектрисам координатных углов (рис. 65); 23) окружность с центром в начале координат и -радиусом 4 (рис. 67); 24) окружность с центром О1 (2; 1)
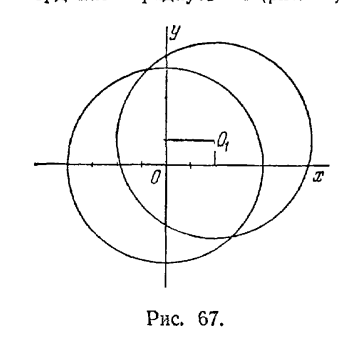
и радиусом 4 (рис. 67); 25) окружность с центром (-5; 1) и радиусом 3; 26) окружность с центром (1; 0) и радиусом 2; 27) окружность с центром (0; -3) и радиусом 1; 28) линия состоит из Одной точки (3; 0) - вырожденная линия; 29) линия состоит из одной точки (0; 0) - вырожденная линия; 30) нет ни одной точки, координаты которой удовлетворяли бы данному уравнению («мнимая линия»); 31) нет ни одной точки, координаты которой удовлетворяли бы данному уравнению («мнимая линия») . 160. Линии 1); 2) и 4) проходят через начало координат. 161. 1) а) (7; 0), (-7; 0);
6) (0; 7), (0; -7); 2) а) (0; 0), (6; 0); б) (0; 0), (0; -8); 3) а) (-10; 0), (-2; 0); б) линия с осью Оу не пересекается; 4) линия с координатными осями не пересекается; 5) а) (0; 0), (12; 0); б) (0; 0), (0; -16); 6) а) линия с осью Ох не пересекается; б) (0; - 1), (0; -7); 7) линия с координатными осями не пересекается. 162. 1) (2; 2),(-2; -2); 2) (1; -1), (9; -9); 3) (3; -4), (1 2/5; -4 4/5 4) линии не пересекаются. 163 Точки М1, М2 и M4 лежат на данной линии;
точки М3 и М5 не лежат на ней. Уравнение определяет окружность (рис. 68). 164. а) (6; π/3); 6) (6; -π/3) в) (3; 0); г) (2√3; π.6); прямая, перпендикулярная к полярной оси и отсекающая на ней считая от полюса, отрезок, равный 3 (рис. 69). 165. а) (1; π/2); б) (2; π/6) и (2; 5/6π) в) (√2; π/4) и (√2; 3/4π); прямая, расположенная в верхней полуплоскости, параллельная полярной оси
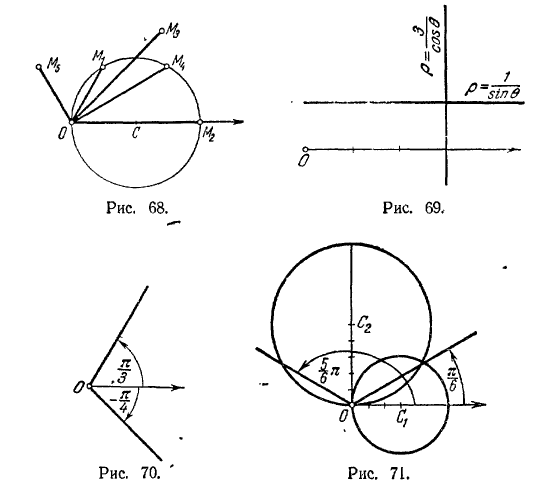
и отстоящая от нее на расстоянии 1 (рис. 69). 166. 1) Окружность с центром в полюсе и радиусом 5; 2) луч, выходящий из полюса, наклоненный к полярной оси под углом π/3 (рис. 70); 3) луч, выходящий из полюса, наклоненный к полярной оси под углом -π/4(риc. 70);
4) прямая, перпендикулярная к полярной оси, отсекающая на ней, считая от полюса , отрезок a = 2; 5) прямая, расположенная в верхней полуплоскости, параллельной полярной оси, отстоящая от нее на расстоянии, равном 1; 6) окружность с центром C2(5; π/2) и радиусом 5 (рис. 71); 8) линия состоит из двух лучей, выходящих из полюса, один из которых наклонен к полярной оси под углом π.6, а другой - под углом - 5/6π (рис. 71); 9) линия состоит из концентрических окружностей с центром в полюсе, радиусы которых r определяются по формуле r = (-l)nπ/6 + πn, где n - любое целое положительное число или нуль.
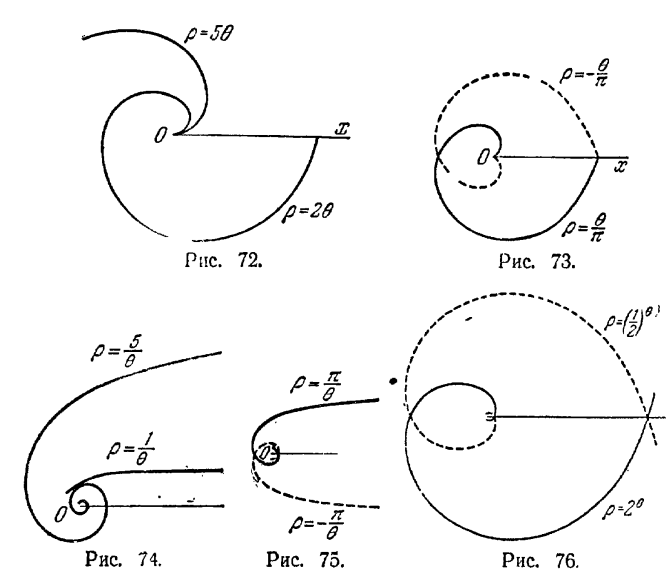
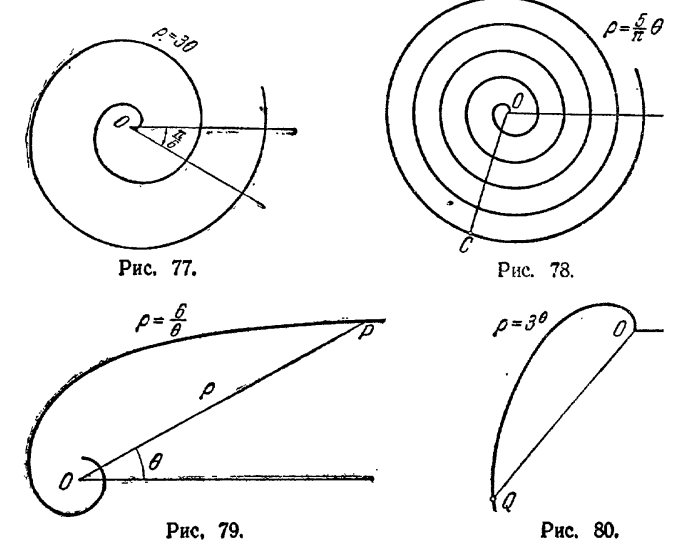
167. Рис. 72 и рис. 73. 168. Рис. 74 и рис. 75. 169. Рис. 76. 170. Отрезок, примыкающий к полюсу, имеет длину, равную π/2; каждый из остальных отрезков имеет длину, равную 6π (рис. 77). 171. На пять частей (рис. 78). 172. (рис. 79). 173. Q (81; 4) (рис. 80). 174. Прямые х ± у = 0. 175. Прямые х ± а = 0. 176. Прямые у ± b = 0. 177. у + 4 = 0. 178. x - 5 = 0. 179. 1) Прямая х - y = 0; 2) прямая х + y = 0: 3) прямая х - 1 = 0; 4) прямая у - 2 = 0. 180. Прямые 4ах ± с = 0, 181. х2 + у2 = r2. 182. (х - α)2 + (у - β)2 = r2. 183. х2 + у2 = 9. 184. х2 + у2 = 16
185. х2 + y2 = а2. 186. (х - 4)2 + у2 = 16. 187. x2/25 + y2/16 = 1. 188. x2/9 - y2/16 = 1. 189. y2 = 2х. 192. y2 = 2рх - парабола. 193. x2/25 + y2/9 = 1 - эллипс. 194. x2/16 - y2/9 = 1 - гипербола. 195. x2/25 + y2/16 = 1 - эллипс. 196. Правая ветвь гиперболы x2/64 + y2/16 = 1. 197. у2 = 20x - парабола. 198. р cos Θ = 3. 199. Θ = π/3. 200. tgΘ = 1.
201. р sin Θ + 5 = 0, р sinΘ - 5 = 0. 202. р = 10 cosΘ. 203 Условию задачи удовлетворяют две окружности, уравнения которых в полярных координатах р + 6 sinΘ = 0, р - 6 sinΘ = 0.
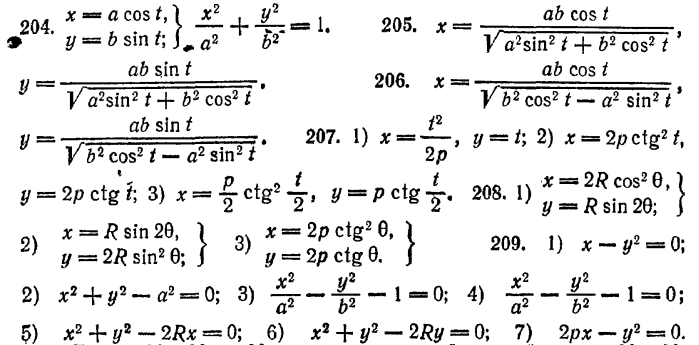
210. Точки M1, М3 и М4 лежат на данной прямой; точки М2, и М3 и M6 не лежат на ней. 211. 3, - 3, 0, -6 и - 12. 212. 1, -2, 4, -5 и 7. 213. (6; 0), (0; -4). 214. (3; -5). 215. A(2; -1), B(-1; 3), С (2; 4). 216. (1; -3), (-2; 5), (5; -9) и (8; -17). 217. 17 кв. ед.
218. C1(-l; 4) или С2(25/7; - 36/7) . 219. C1(l; -1) или С2(-2; -10). 220. 1) 2х - Зу + 9 = 0; 2) Зх - у = 0; 3) у + 2 = 0; 4) Зх + 4у - 12 = 0; 5) 2х + у + 5 = 0; 6) х + Зу -2 = 0. 221. 1) k = 5, b = 3; 2) k = -2/3, b = 2; 3)k = -5/3, b = -2/3, 4) k = - 3/2, b = 0; 5) k = 0, b = 3. 222. 1) -5/3; 2)3/5
223. 1) 2х + Зу - 7 = 0; 2) Зх - 2у - 4 = 0. 224. Зх + 2у = 0, 2х - 3у - 13 = 0. 225. (2; 1), (4; 2), (-1; 7), (1; 8). 226. (-2; -1). 227. Q(11; -11). 228. 1) 3x - 2у - 7 = 0; 2) 5х + у - 7 = 0; 3) 8х+12у + 5 = 0; 4) 5х + 7у + 9 = 0; 5) 6х - 30у - 7 = 0.
229. a) k = 7; б) k = 7/10; в) k = -3/2 230. 5х - 2у - 33 = 0, х + 4у - 11 = 0, 7х + 6у + 33 = 0. 231. 7х - 2у - 12 = 0, 5х + у - 28 = 0, 2х - 3у - 18 = 0. 232. 2x + у + 1 = 0. 233. 2х + Зу - 13 = 0. 234. 4х + Зу - 11 = 0, х + y + 2 = 0, Зх + 2у - 13=0. 235. (3; 4). 236. 4х + у - 3 = 0. 237. х - 5 = 0. 238. Уравнение стороны АВ: 2х + y - 8 = 0; ВС: х + 2у - 1 = 0; СА: х - у - 1 = 0. Уравнение медианы, проведенной из вершины А: х - 3 = 0; из вершины В: х + у - 3 = 0; из вершины С: у - 0. 239. (-7; 0); (0:+21/3). 242. (1; 3). 243. 3x - 5у + 4 = 0, х + 7у - 16 = 0,
Зх - 5у - 22 = 0, х + 7у + 10 = 0. 244. Уравнения сторон прямоугольника: 2х - 5у + 3 = 0, 2х - 5у - 26 = 0; уравнение его диагонали: 7х - Зу - 33 = 0. 245. 5х + y - 3 = 0 - биссектриса внутреннего угла; х - 5у - 11 = 0 - биссектриса внешнего угла. 246. х + у - 8 = 0; 11х - у - 28 = 0. Указание. Условию задачи удовлетворяют две прямые: одна из них проходит через точку Р и середину отрезка, соединяющего топки А и B; другая проходит через точку Р параллельно отрезку АВ. 247. (-12; 5). 248. M1 (10; -5).
249. P(5/3; 0). Указание. Задача может быть решена по следующей схеме: 1) устанавливаем, что точки М и N расположены по одну сторону оси абсцисс; 2) находим точку, симметричную одной из данных точек относительно оси абсцисс, например точку N1 симметричную точке М и 3) составляем уравнение прямой, проходящей через точки М и N1; 4) решая совместно найденное уравнение с уравнением оси абсцисс, получим координаты искомой точки.
250. Р (0; 11). 251. Р(2; -1), 252. Р (2; 5). 253. 1)φ = π/4;
2) φ = π/2; 3) φ = 0 - прямые параллельные; 4) φ = arctg16/11
254. х - 5у + 3 = 0 или 5х + y - 11 = 0. 255. Уравнения сторон квадрата: 4х + Зу + 1=0, Зх - 4у + 32 = 0, 4х + Зу - 24 = 0, Зх - 4у + 7 = 0; уравнение его второй диагонали: х + 7у - 31 = 0. 256. Зх - 4у + 15 = 0, 4х + Зу - 30 = 0, Зх - 4у - 10 = 0, 4х + Зу - 5 = 0. 257. 2х + y - 16 = 0, 2х + y + 14 = 0, х - 2у - 18 = 0. 258. Зх - у + 9 = 0, Зх + y + 9 = 0. 259. 29х - 2у + 33 = 0. 262. 1) Зх - 7у - 27 = 0; 2) х + 9у + 25 = 0; 3) 2х - Зу - 13 = 0; 4) х - 2 = 0; 5) у + 3 = 0. 264. Перпендикулярны 1), 3) и 4). 266. 1) φ = 45°; 2) φ = 60°; 3) φ = 90°. 267. М3 (6; -6). 268. 4х - у - 13 = 0, х - 5 = 0,
x + 8y + 5 - 0. 269. ВС: Зх + 4у - 22 = 0; СА: 2x - 7y - 5 = 0 CN: Зх + 5y - 23 = 0. 270. х + 2у - 7 = 0, х - 4у - 1 = 0, х - y - 2 = 0.
Указание. Задача может быть решена по следующей схеме:
1. Устанавливаем, что вершина А не лежит ни на одной из данных прямых. 2. Находим точку пересечения медиан и обозначаем ее какой-нибудь буквой, например М. 3. На прямой, проходящей через точки А и М, строим отрезок MD = AM (рис. 81). Затем определяем координаты точки D, зная точку М - середину отрезка AD и один из его концов А.
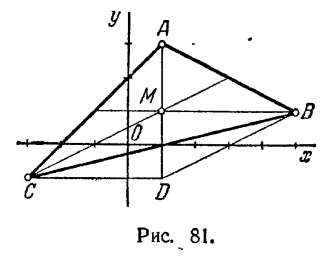
4. Устанавливаем, что четырехугольник BDCM - параллелограмм (его диагонали взаимно делятся пополам), составляем уравнения прямых DB и DC. 5. Вычисляем координаты точек В и С. 6. Зная координаты всех вершин треугольника, мы можем составить уравнения его сторон.
271. Зх - 5у - 13 = 0, 8х - Зу + 17 = 0, 5х + 2у - 1 = 0. 272. 2х - у + 3 = 0, 2х + у -7 = 0, х - 2у - 6 = 0. Указание. Если на одной из сторон угла дана точка А, то точка, симметричная точке А относительно биссектрисы этого угла, будет лежать на другой его стороне.
273. 4х - 3у + 10 = 0,7х + у - 20 = 0, Зх + 4у - 5 = 0. 274. 4х + 7у - 1 = 0, y - 3 = 0, 4х + Зу - 5 = 0. 275. Зх + 7у - 5 = 0, Зх + 2y - 10 = 0, 9х + 11у + 5 = 0. 276. х - Зу - 23 = 0, 7х + 9у + 19 = 0, 4х + 3у + 13 = 0, 277. х + у - 7 = 0, х + 7у + 5 = 0, х - 8у + 20 = 0. 278. 2х + 9у - 65 = 0, 6х - 7у - 25 = 0, 18х + 13у - 41 =0. 279. х + 2у = 0, 23х + 25у = 0. 280. 8х - у - 24 = 0. 283. 3х + у = 0, х - Зy = 0. 284. Зх + 4у - 1 = 0, 7х + 24у - 61 = 0. 285. 1) а = -2, 5у - 33 = 0: 2) а1 = -3, x - 56 = 0; a2 = 3, 5х + 8 = 0; 3) а1 = 1, 3х - 8y = 0; а2 = 5/3
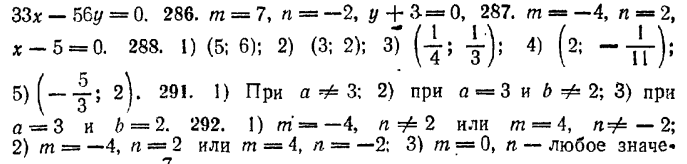
ние. 293. m = 7/12. 294. Условию задачи удовлетворяют два значения m: m1 = 0, m2 = 6. 295. 1) Пересекаются; 2) не пересекаются; 3) не пересекаются. 298. а = -7. 299. 1) x/3 + y/2 =1; 2 ) x/-6 + y/8 = 1; 390. 6 кв. ед. 301. х + у + 4 = 0. 302 Зх - 2у - 0. 303, Решение. Напишем «в отрезках»:
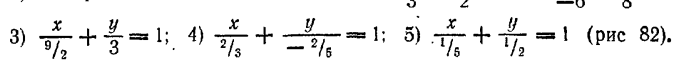
300. 6 кв. ед. 301. x + y + 4 = 0. 302. x =y -5 = 0, x - y + 1 = 0, 3x - 2y = 0. 303. Решение. Напишем уравнение искомой прямой "в отрезках"
x/a + y/b = 1 (1)
Наша задача - определить значения параметров а и b. Точка C(l; 1) лежит на искомой прямой, следовательно, ее координаты должны удовлетворять уравнению (1). Подставим в уравнение (1) вместо текущих координат координаты точки С; после приведения к общему знаменателю получим:
a + b = ab (2)
Теперь заметим, что площадь треугольника S, отсекаемого прямой от координатного угла, определяется формулой ±S = ab/2; + S в том случае, когда отрезки а и b одного знака, и -S в том случае, когда эти отрезки разных знаков. Согласно условию нашей задачи будем иметь:
ab = ± 4 (3)
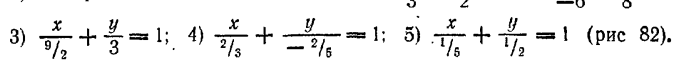
а3 = -2 - 2√2, b3 = -2 + 2√2. Таким образом, условию задачи удовлетворяют трй прямые. Подставим в уравнение (1) полученные Решим систему уравнений a и b: x/(-2 + 2√2 ) +y(-2 - 2√2 ) = 1, x/(-2 - 2√2 ) + y(-2 + 2√2 ) = 1
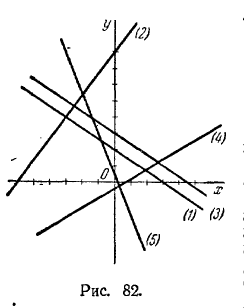
После упрощения этих уравнений получим: х + у - 2 = 0, (l + √2) х + (l - √2)y - 2 = 0, (1 - √2) + (1 + √2)у - 2 = 0.‘ 304. Условию задачи удовлетворяют следующие три прямые: (√2 + 1) x + (√2 - l) у - 10 = 0, (√2 - 1)x + (√2+ l)y + 10 = 0, х - у - 10 = 0. 305. 3х - 2у - 12=0, Зх - 8у + 24 = 0.
306. x + Зу - 30 = 0, Зх + 4у - 60 = 0, Зх - у - 30 = 0, х - 12у + 60 = 0. 307. Условию задачи удовлетворяют две прямые, пересекающие соответственно оси координат в точках (2; 0).
(0; -3) и (-4; 0), (0; 3/2). 308. s ≥ 2x1y1. 309. Прямые 1), 4), 6) и 8) заданы нормальными уравнениями.
310. 1)-4/5х - 3/5у - 2 = 0; 2) - 4/5 х + 3/5у - 10 = 0; 3) -12/13x + 5/13y - 1 = 0; 4) - х - 2 = 0; 5) 2/√5x - 1/√5y - 1 = 0.
311. 1)α = 0, p = 2; 2) α = π, p = 2; 3) α =π/2, p = 3; 5) α = π/6, p = 3; 6) α = - π/4, p = √2; 7) α = -2/3π, p = 1; 8) α = - β, p = q; 9) α = β - π, p = q. 312. 1) δ = -3, d = 3; 2) δ = 1, d = 1; 3) δ = -4, d = 4; 4) δ = 0, d = 0 - точка Q лежит на прямой. 313. 1) По одну сторону; 2) по разные стороны; 3) по одну сторону; 4) по одну сторону; 5) по разные стороны. 314. 5 кв. ед.
315. 6 кв. ед. 318. Является выпуклым. 319. Не является выпуклым. 320. 4. 321. 3. 322. 1) d = 2,5; 2) d = 3; 3) d = 0,5; 4) d = 3,5. 323. 49 кв. ед. 325. В отношении 2 : 3, считая от второй прямой. 326. Решение. Задача о проведении прямых через точку Р на расстоянии, равном 5 от точки Q, равносильна задаче о проведении из точки Р касательных к окружности радиуса 5, с центром в Q. Вычислим расстояние QP: QP = √((2 - 1)2 + (7 - 2)2) = √26. Мы видим, что расстояние QP больше радиуса окружности; следовательно, из точки Р можно провести две касательные к этой окружности. Теперь перейдем к составлению их уравнений. Уравнение всякой прямой, проходящей через точку Р, имеет вид
у - 7 = k(x - 2) (1)
или kx - у + 7 - 2k = 0, где k - пока неопределенный угловой коэффициент. Приведем это уравнение к нормальному виду. С этой целью находим нормирующий множитель μ = ± 1/(k2 + 1). Умножая уравнение (1) на μ, получим искомое нормальное уравнение
(kx - y + 7 - 2k)/±√(k2 + 1) = 0 (2)
Подставляя в левую часть уравнения (2) координаты точки Q, имеем: |k - 2 + 7 - 2k| /√(k2 = 5. Решая это уравнение, найдем два значения k: k1 - 5/12, k2 = 0. Подставляя найденные значения углового коэффициента в уравнение (1), получаем искомые уравнения: 5х + 12у - 94 = 0 и у - 7 = 0. Задача решена.
327. 7х + 24у - 134=0, х - 2 = 0. 328. Зх + 4y - 13 = 0. 330. 8x - 15у + 9 = 0. 331. 3х - 4у - 25 = 0, 3х - 4у + 5 = 0. 332. Условию задачи удовлетворяют два квадрата, симметрично расположенных относительно стороны АВ. Уравнения сторон одного из них: 4х + Зу - 8 = 0, 4х + 3 у + 17 = 0, 3х - 4у - 6 = 0, 3х - 4у + 19 = 0, Уравнения сторон другого: 4х + 3у - 8 = 0, 4х + 3у - 33 = 0, Зх - 4у - 6 = 0, 3х - 4у + 19 = 0. 333. Условию задачи удовлетворяют два квадрата; остальные стороны одного из них лежат на прямых: Зх + 4у - 11 = 0, 4х - 3у - 23 = 0, Зх + 4у - 27 = 0; остальные стороны другого - на прямых: 3х + 4у - 11 = 0, 4х - Зу - 23 = 0, 3х + 4у + 6 = 0.
334. Зх + 4у + 6 = 0, Зх + 4у - 14 = 0 или Зх + 4у + 6 = 0, Зх + 4у + 26 = 0. 335. 12х -5у + 61=0, 12х - 5у + 22 = 0 или 12х - 5у + 61 = 0, 12х - 5у + 100 = 0. 336. M(2; 3). 337. 4х + у + 5 = 0, у - 3 = 0. 338. 1) Зх - у + 2 = 0; 2) х - 2у + 5 = 0; 3) 20х - 8у - 9 = 0. 339. 1) 4х - 4у + 3 = 0, 2х + 2у - 7 = 0; 2)4х + 1 = 0, 8у + 13 = 0; 3) 14х - 8у - 3 = 0, 64х + 112у - 23 = 0. 340. х - Зу - 5 = 0, Зх + у - 5 = 0. Указание. Искомые прямые проходят через точку Р перпендикулярно к биссектрисам углов, образованных двумя данными прямыми. 341. 1) В одном углу; 2) в смежных углах; 3) в вертикальных углах.
342. 1) В вертикальных углах; 2) в смежных углах; 3) в одном углу. 343. Внутри треугольника. 344 Вне треугольника. 345. Острый угол. 346. Тупой угол. 347. 8х + 4y - 5 = 0. 348. x + 3y - 2 = 0. 349. 3х - 19 = 0. 350. 10x - 10y - 3 = 0. 351. 7х + 56y - 40 = 0. 352. х + у + 5 = 0. 353. S(2; -1). 354. 1) Зх + 2у - 7 = 0; 2) 2х - у = 0; 3) у - 2 = 0; 4) х - 1 = 0; 5) 4х + 3у - 10 = 0; 6) 3х - 2у + 1 = 0.
355. 74х + 13у + 39 = 0. 356. х - у - 7 = 0. 357. 7х + 19y - 2 = 0. 358. х - у + 1 = 0, 359. 4х - 5у + 22 = 0, 4х + у - 18 = 0, 2х - у + 1 = 0. 360. х - 5y + 13 = 0, 5х + у + 13 = 0. 361. 5х - у - 5 = 0 (ВС), х - у + 3 = 0 (AС), Зх - у - 1 =0 (CN). 362. х - 5у - 7 = 0, 5х + у + 17 = 0, 10х + 7y - 13 = 0. 363. 2х + у + 8 = 0, x + 2y + 1=0. 366. С = -29. 367. а ≠ -2; 368. Уравнения сторон квадрата: 4х + 3у - 14 = 0, 3х - 4у + 27 = 0, Зх - 4у + 2 = 0, 4х + 3y + 11 = 0; уравнение его второй диагонали: 7х - у + 13 = 0. 369. х + у + 5 = 0. 370. х + y + 2 = 0, х - у - 4 = 0, 3х + у = 0. 371. 2х + у - 6 = 0, 9х + 2y + 18 = 0. 372. Зx - y + 1 = 0. 374. Зх - 4у + 20 = 0, 4х + 3у - 15 = 0. 375. х + 5у- 13 = 0, 5x - y + 13 = 0. 376. Условию задачи удовлетворяют две прямые: 7х + у - 9 = 0, 2х + y + 1=0. 377. 5х - 2у - 7 = 0. 378. АС: 3х + 8y - 7 = 0, BD: 8х - 3у + 7 = 0. 379. 4х + y + 5 = 0, х- 2у - 1 = 0, 2х + 5y - 11 = 0.
381. 1) р sin (β - Θ) = р, psin(π/6 - Θ) = 3; 2) р cos (Θ - α) = a cosα, р cos (Θ + 2/3π) = - 1; 3) p sin(β - Θ) = а sinβ, р sin(π/6 - Θ) = 3.
382. р sin (β - Θ) = p1 sin (β - Θ1). 383. р cos (Θ - α) = p1 cos (Θ,1 - α).
384. p sin (Θ - Θ1)/p2 sin (Θ2 - Θ1)= √(p2 + p21 - 2pp1cos(Θ - Θ1))/√(p22 + p21 - 2p2p1cos(Θ - Θ1))
385. 1) x2 + y2 = 9; 2) (х - 2)2 + (у + 3)2 = 49; 3) (х - 6)2 + (y + 8)2 = 100; 4) (х + 1)2 + (y - 2) = 25; 5) (х- 1)2 + (р - 4)2 = 8; 6) х2 + у2 = 16; 7) (х - 1)2 + (y + 1)2 = 4; 8) (х - 2)2 +(y - 4)2 =10; 9) (х - 1)2 + y2 = 1; 10) (х - 2)2 + (y - 1)2 = 25. 386. (х - 3)2 + (у + 1)2 = 38.
387. (х - 4)2 + (у + 1 )2 = 5 и (х - 2)2 + (у - З)2 = 5. 388. (х + 2)2 + (y + 1)2 = 20. 389. (х - 5)2 + (y + 2)2 = 20 и (х - 9/5)2 + (у - 22/5)2 = 20. 390. (х - 1)2 + (у + 2)2 =16. 391. (х + 6)2 + ( y - 3)2 = 50 и (х - 29)2 + (у + 2)2 - 800. 392. (х - 2)2 + (y - 1)2 = 5 , (x - 22/5)2 + (y + 31/5)2 = 289/5.
393. (х - 2)2 + {у - 1)2 = (y - 1)2 = 81/13 и (x + 8)2 + (y + 7)2 = 25/13. 394. (x - 2)2 + (y - 1)2 = 25 и (x + 202/49)2 + (y - 349/49)2 = (185/49)2 395. (x + 10/7)2 + ( y + 25/7)2 = 1 и (x - 30/7)2 + (y - 5/7)2 = 1. 396. (х - 5)2 + y2 = 16, (х + 15)2 + y2 = 256, (x - 35/3 )2 + (y + 40/3)2 = (32/3)2.
397. Уравнения 1), 2), 4), 5), 8) и (10) определяют окружности; C (5; -2), R = (5; 2) С (-2; 0), R = 8; 3) уравнение определяет единственную точку (5; -2); 4) С (0; 5), R = √5 ; 5) С (1; -2), R = 5; 6) уравнение не определяет никакого геометрического образа на плоскости; 7) уравнение определяет единственную точку (-2, 1).
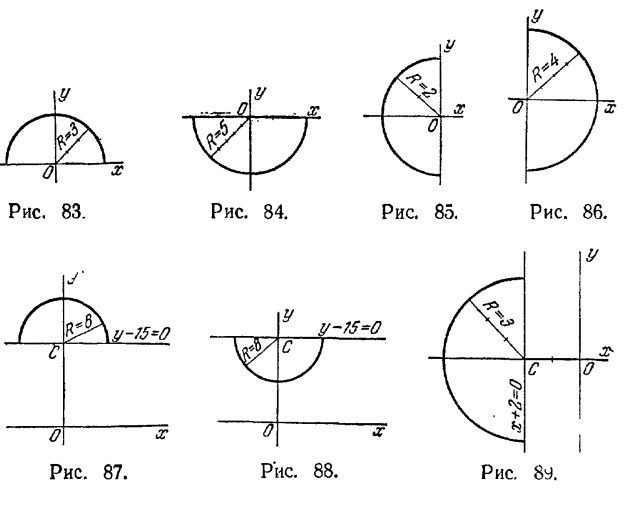
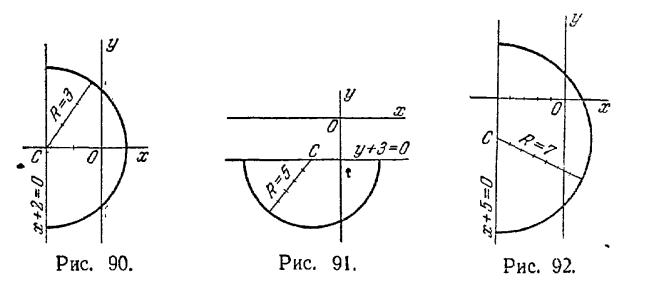
8) С ( -1/2; 0), R = 1/2; 9) уравнение не определяет никакого геометрического образа на плоскости; 10) С (0; - 1/2), R = 1/2.
398. 1) Полуокружность радиуса R = 3 с центром в начале коор- динат, расположенная в верхней полуплоскости (рис. 83); 2) полуокружность радиуса R = 5 с центром в начале координат, расположенная в нижней полуплоскости (рис. 84); 3) полуокружность радиуса R - 2 с центром в начале координат, расположенная в левой Полуплоскости (рис. 85); 4) полуокружность радиуса R = 4 с центром в начале координат, расположенная в правой полуплоскости (рис. 86);
5) полуокружность радиуса R = 8 с центром С (0; 15), расположенная над прямой y - 15 = 0 (рис. 87); 6) полуокружность радиуса R = 8 с центром С (0; 15), расположенная под прямой у - 15 = 0 (рис. 88); 7) полуокружность радиуса y = 3 с центром С (- 2; 0), расположенная влево от прямой х + 2 = 0 (рис. 89); 8) полуокружность радиуса R - 3 с центром С (-2; 0), расположенная вправо от прямой х + 2 = 0 (рис. 90); 9) полуокружность радиуса R = 5 с центром С (-2; -3), расположенная под прямой y + 3 = 0 (рис. 91);
10) полуокружйость радиуса R = 7 с центром С (-5; -3), расположенная вправо от прямой х+5 = 0 (рис. 92). 399. 1) Вне окружности; 2) на окружности; 3) внутри окружности; 4) на окружности; 5) внутри окружности. 400. I) х + 5у - 3 = 0; 2) * + 2 = 0; 3) Зх - у - 9 = 0; 4) */+1=0. 401. 2*-5у+ 19 = 0. 402. а) 7; 6) 17; в) 2. 403. Л+(-1; 5) и М2{-2;-2). 404. I) Пересекает окружность; 2) касается окружности; 3) проходит вне окружности.
10) полуокружйость радиуса R = 7 с центром С (-5; -3), расположенная вправо от прямой х + 5 = 0 (рис. 92). 399. 1) Вне окружности; 2) на окружности; 3) внутри окружности; 4) на окружности; 5) внутри окружности. 400. I) х + 5у - 3 = 0; 2) x + 2 = 0; 3) Зх - у - 9 = 0; 4) y + 1 = 0. 401. 2x - 5у + 19 = 0. 402. а) 7; б) 17; в) 2. 403. M1(-1; 5) и М2(-2;-2). 404. 1) Пересекает окружность; 2) касается окружности; 3) проходит вне окружности.
405. 1) | k| < 3/4 2) k = ± 3/4 3) |k| > 3/4. 406. b2/(1 + k)2 = R2
407. 2х + у - 3 = 0. 408. 11х - 7y - 69 = 0. 409. 2√5. 410. 2x -3y + 8 = 0, 3x + 2y - 14 = 0. 412. х2 + у2 + 6x - 9у - 17 = 0. 413. 13х2 + 13у2 + 3х + 71y = 0. 414. 7х - 4у = 0. 415.2. 416.10.
417. (x + 3)2 + (y - 3)2 = 10. 418. x - 2y + 5 = 0. 419. 3x - 4у+ 43 = 0. 420. M 1 (-7/2; 5/4); , d = 2√5. 421. x1x + y1y = R2 422. (x1 - α)(x - α) + (y1 - β) (y - β) = R2. 423. 45°. 424. 90°. 425. (α1 - α2)2 + (β1 - β2)2 = R21 + R22 427. x - 2у - 5 = 0 и 2x - у - 5 = 0. 428. 2x + у - 8 = 0 и x - 2y + 11 = 0. 429. 2x + y - 5 = 0, x - 2y = 0. 430. 90°. 431. x + 2y + 5 = 0. 432. d = 7,5.
433. d = 7. 434. d = √10. 435. 3. 436. 2х + y - 1= 0 и 2x + y + 19 = 0. 437. 2x + y - 5 =0 и 2x + y + 5 = 0. 438. p = 2Rcos (Θ - Θ0) (рис. 93). 439. 1) p = 2RcosΘ (рис. 94); 2) p = -2RcosΘ (рис. 95); 3) p = 2 R sinΘ (рис. 96); 4) p = -2R sinΘ (рис. 97). 440. 1) (2; 0) и R = 2; 2) (3/2 ; π/2) и R = 3/2; 3) (1; π) и R = 1; 4) (5/2; -π/2) и R = 5/2; 5) (3; π/3) и R = 3; 6) (4; 5/6π) и R = 4; 7) (4; -π/6) и R = 4. 441. 1) x2 + y2 - Зх = 0; 2) x2 + у2 + 4y = 0; 3) x2 + y2 - x + y = 0.
442. 1) p = cosΘ; 2) p = - 3 cosΘ; 3) p = 5 sinΘ; 4) p = - sinΘ; 5) p = cosΘ + sinΘ. 443. p = R sec (Θ - Θ0) 444. 1) x2/25 + y2/4 = 1; 2) x2/25 + y2/9 = 1; 3) x2/169 + y2/144 = 1; 4) x2/25 + y2/16 = 1; 5) x2/100 + y2/64 = 1; 6) x2/169 + y2/25 = 1; 7) x2/64 + y2/48 = 1, 8)x2/16 + y2/12 = 1; 9) x2/13 + y2/9 = 1 или x2/(117/4) + y2/9; 10) x2/25 + y2/169 = 1;
445. 1) x2/4 + y2/49 = 1; 2) x2/9 + y2/25 = 1; 3) x2/25 + y2/169 = 1; 4) x2/64 + y2/100 = 1; 5) x2/16 + y2/25 = 1; 6) x2/7 + y2/16 = 1.
446. 1) 4 и 3; 2) 2 и 1; 3) 5 и 1; 4) √5 и √3; 5) 5/2 и 5/3 6) 1/3 и 1/5; 7) 1 и 1/2;
8) 1 и 4; 9) 1/5 и 1/3 10) 1/3 и 1. 447. 1) 5 и 3; 2) F1 (-4; 0), F2 (4; 0); 3) ε = 4/5|; 4) x = ± 25/4. 448. 16 кв. ед. 449. 1) √5 и 3;
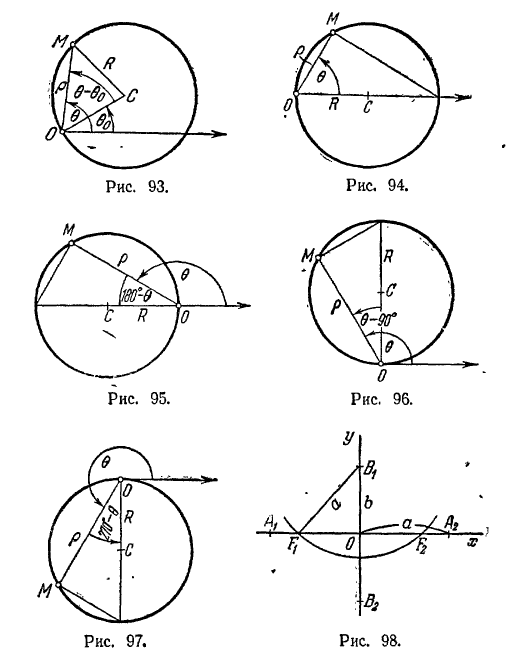
2) F1 (0; -2), F (0; 2); 3) ε = 2/3; 4) у = ± 9/2. 450. 4√5/45 кв. ед. 451. b2/c. 452. См. рис. 98. 453. (-3;- 8/5), (-3; 8/5) 454. Точки А1 и A6 лежат на эллипсе; A2, A4 и A8 - внутри эллипса; A3, A5, A7, A9, A10 - вне эллипса. 455. 1) Половина эллипса x2/16 + y2/9 = 1, расположенная в верхней полуплоскости (рис. 99);
2) половина эллипса x2/9 + y2/25 = 1, расположенная в нижней полуплоскости (рис. 100); 3) половина эллипса x2/4 + y2/9 = 1, расположенная в левой полуплоскости (рис. 101); 4) половина эллипса х2 + y2/49 = 1, расположенная в правой полуплоскости (рис. 102).
456. 15. 457. 8. 458. 5х + 12y + 10 = 0, х - 2 = 0. 459. r1 = 2,6, r2 = 7,4. 460. 20. 461. 10. 462. (-5; 3√3) и (-5; -3√3) 463. (-2; √21/2) и (-2; - √21/2)
464. 3 и 7. 465. 1) x2/36 + y2/9 = 1; 2) x2/16 + y2/(16/3) = 1; 3) x2/20 + y2/15 = 1; 4) x2/20 + y2/4 =1; 5) x2/9 + y2/5 = 1; 6) x2/256 + y2/192 = 1; 7) x2/15 + y2/6 =1. 466. 1) √3/2; 2) √2/2 3) √3/3; 4) 1/2.
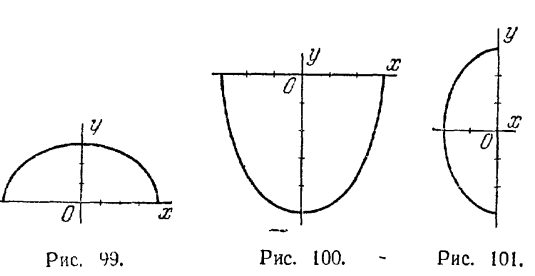
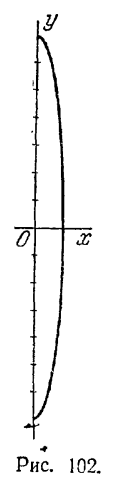
467. ε = √2/2. 468. (x - x0)/a2 + (y - y0)/b2 = 1. 469. (x - 3)2/9 + (y + 4)2/16 = 1. 470. (x + 3)2/9 + (y - 2)2/4 = 1.
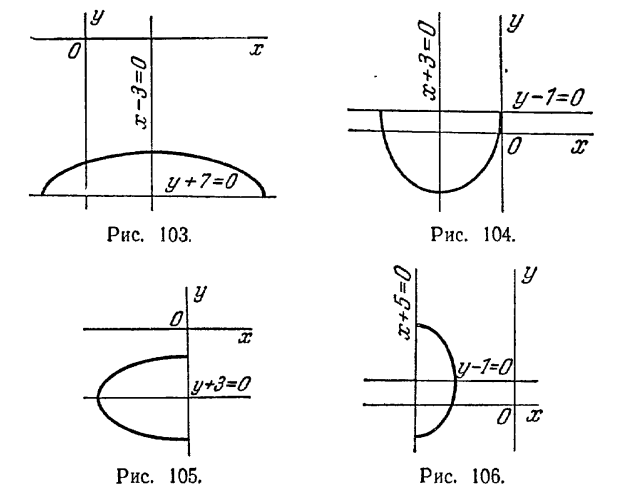
471. 1) С (3; -1), полуоси 3 и √5, ε = 2/3, уравнения директрис: 2х - 15 = 0, 2х + 3 = 0; 2) С(-1;2), полуоси 5 и 4, ε = 3/5, уравнения директрис: Зх - 22 = 0, Зх + 28 = 0; 3) С (1; -2), полуоси 2√3 и 4, ε = 1/2, уравнения директрис: y - 6 = 0, y + 10 = 0. 472. 1) Половина эллипса (x - 3)2/25 + (y + 7)2/4 = 1, расположенная над прямой y + 7 = 0 (рис. 103); 2) половина эллипса (x + 3)2/9 + (y - 1)2/16 = 1, расположенная пол прямой y - 1 = 0 (рис. 104);
3) половина эллипса x2/16 + (y + 3)2/4 = 1 расположенная в левой полуплоскости (рис. 105); 4) половина эллипса (x + 5)2/4 + (y - 1)/9 = 1, расположенная вправо от прямой x + 5 = 0 (рис. 106).
473. 1) (x - 2)2/169 + y2/25 = 1; 2) 2х2 - 2ху + 2y2 - 3 = 0; 3) 68х2 + 48xy + 82y2 - 625 = 0; 4) 11х2 + 2xy + 11y2 - 48х - 48y - 24 = 0.
474. 5x2 + 9y2 + 4х - 18y - 55 = 0. 475. 4х2 + 3y2 + 32х - 14y + 59 = 0. 476. 4х2 + 5y2 + 14х + 40y + 81 = 0. 477. 7х2 - 2ху + 7y2 - 46x + 2y + 71 = 0. 478. 17x2 + 8xy + 23y2 + 30x - 40y - 175 = 0.
479. х2 + 2y2 - 6х + 24y + 31 = 0. 480. (4; 3/2), (3; 2). 481. (3; 8/5) - прямая касается эллипса. 482. Прямая проходит вне эллипса. 483. 1) Прямая пересекает эллипс; 2) проходит вне эллипса;3) касается эллипса.
484. 1) При |m| < 5 - пересекает эллипс; 2) при m = ±5 - касается эллипса; 3) при |m| > 5 - проходит вне эллипса. 485. k2a2 + b2 = m2. 486. x1x/a2 + y1y/b2 = 1. 488. 3х + 2y - 10 = 0 и 3х + 2y - 10 = 0 489. х + y - 5 = 0 и х + y + 5 = 0. 490. 2х - y - 12 = 0, 2х - y + 12 = 0; d = 24√5/5, 491. М1 (-3; 2); d = √13. 492. х + y - 5 = 0 и x + 4y - 10. 493. 4х - 5y - 10 = 0. 494. d = 8. 495. x2/20 + y2/5 = 1 или x2/80 + 4y2/5 = 1. 496. x2/40 + y2/10 = 1. 499. x2/17 + y2/8 = 1. Указание. Воспользоваться свойством эллипса, сформулированным в задаче 498.
500. x2/25 + y2/4 = 1. Указание. Воспользоваться свойством эллипса, сформулированным в задаче 498.
502. 2x + 11y - 10 = 0. Указание. Воспользоваться свойством эллипса, сформулированным в задаче 501. 503. (3; 2) и (3; -2),
504. R = mn√2/ √(m2 + n2) 505. 10,5 √3. 506. φ = 60°. 507. 16,8. 508. 60°. 509. В эллипс, уравнение которого x2/25 + y2/16 = 1.
510. х2 + y2 = 9. 511. x2/36 + y2/16 = 1. 512. q = 4/3. 513. q = 2/3. 514. q1 = 4/3, q2 = 4/5. 515. 1) x2/25 - y2/16 = 1; 2) x2/9 - y2/16 = 1; 3) x2/4 - y2/5 = 1; 4) x2/64 - y2/36 = 1; 5) x2/36 - y2/64 = 1; 6) x2/144 - y2/25 = 1; 7) x2/16 - y2/9 = 1; 8) x2/4 - y2/5 = -1; 9) x2/64 - y2/36 = 1. 516. 1) x2/36 - y2/324 = -1; 2) x2/16 - y2/9 = -1; 3) x2/100 - y2/576 = -1; 4) x2/24 - y2/25 = -1; 5) x2/9 - y2/16 = -1; 517. 1) a = 3, b = 2; 2) a = 4, b = 1; 3) a = 4, b = 2; 4) a = 1, b = 1; 5) a = 5/2, b = 5/3; 6) a = 1/5, b = 1/4; 7) а = 1/3 , b = 1/8 .
518. 1) a = 3, b = 4; 2) F1(-5; 0), F2(5 ; 0) 519. 1) а = 3, b= 4 2) F1(0;-5), F2 (0; 5); 3) ε = 5/4 4)y = ±4/3x, 5) y = ± 16/5.
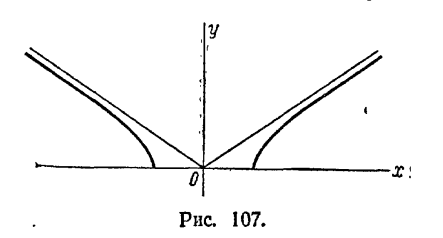
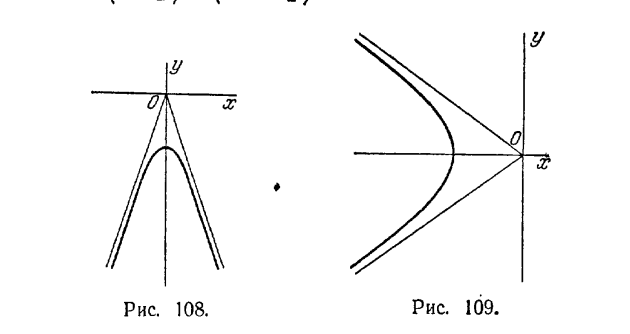
520. 12 кв. ед. 521. 1) Часть гиперболы x2/9 - y2/4 = l, расположенная в верхней полуплоскости (рис. 107); 2) ветвь гиперболы х2 - y2/9 = -1, расположенная в нижней полуплоскости (рис. 108); 3) ветвь гиперболы x2/16 - y2/9 = 1 расположенная в левой полуплоскости (рис. 109); 4) веть гиперболы x2/25 - y2/4 = -1 расположенная в верхней полуплоскости (рис. 110), 522. х = 4√5 у + 10 = 0 и x - 10 = 0. 523. r1 = 2 1/4, r2 = 10 1/4. 524. 8. 525. 12. 526. 10. 527. 27. 528. (10; 9/2) и (10; -9/2). 529. (-6; 4√3) и (-6; - 4√3).
530. 2 1/12 и 26 1/2. 531. См. рис. 111. 532. 1) x2/32 - y2/8 = 1; 2) x2 -y2 = 16; 3) x2/18 - y2/8 = 1; 4) x2/4 - y2/5 = 1 или x2/(61/9) - y2/(305/16) = 1; 5) x2/16 - y2/9 = 1. 533. ε = √2. 534. ε = √3. 535. x2/4 - y2/12 = 1. 536. x2/60 - y2/40 = 1. 540. 1) (x - x0)2/a2 - (y - y0)2/b2 = 1; 2) (x - x0)2/a2 - (y - y0)2/b2 = -1;
541. I) С (2; -3), a = 3, b = 4, ε = 5/3, уравнения директрис: 5x - 1 = 0, 5x- 19 = 0, уравнения
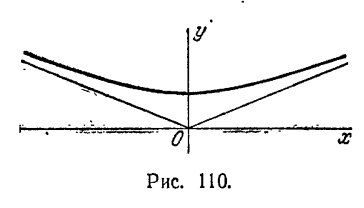
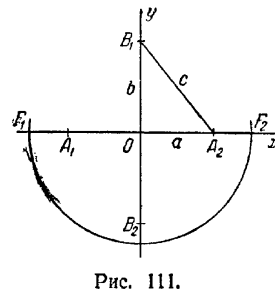
асимптот; 4x - 3у - 17 = 0, 4x + 3у + 1 = 0; 2) С (-5; 1), а = 8, b = 6, ε = 1,25, уравнения директрис: х = - 11,4 и x = 1,4, уравнения асимптот: 3x + 4y + 11 = 0 и 3х - 4у + 19 = 0; 3)С(2;-1), a = 3, b = 4, ε = 1,25, уравнения директрис: у = - 4,2, у = 2,2, уравнения асимптот: 4х + 3у - 5 = 0, 4х - 3y - 11 = 0. 542. 1) Часть гиперболы (x - 2)2/9 - (y + 1)2/4 = 1, расположенная над прямой y + 1 = 0 (рис. 112); 2) ветвь гиперболы (x - 3)2/4 - (y - 7)2/9 = -1,
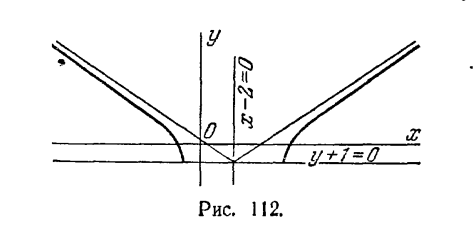
расположенная под прямой y - 7 = 0 (рис. 113); 3) ветвь гиперболы (х - 9)2/16 - (y + 2)2/4 = 1, расположенная влево от прямой х - 9 = 0 (рис. 114); 4) часть гиперболы (х - 5)2/9 - (y + 2)2/16 = -1, располо-
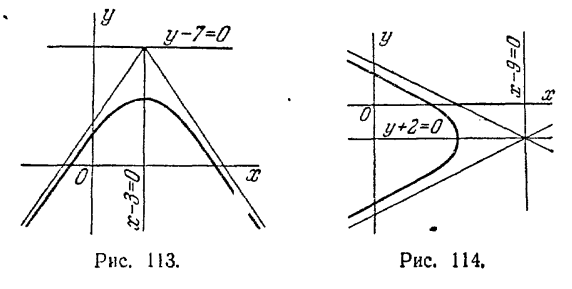
женная влево от прямой х - 5 = 0 (рис. 115). 543, 1) (x - 3)2/144 - (y - 2)2/25 = 1; 2) 24ху + 7y2 - 144 = 0; 3) 2ху + 2х - 2у + 7 = 0. 544. x2/16 - y2/9 = 1. 545.x2/25 - y2/144 = - 1. 546. x2 - 4у2 - 6x - 24y - 47 = 0. 547. 7х2 - 6ху - y2 + 26x - 18y - 17 = 0. 548. 91x2 - 100xу + 16y2 - 136x + 86y - 47 = 0. 549. ху = a2/2 при повороте старых осей на угол -45° ; xy = -a2/2 при повороте на угол +45°.
550. 1) С (0; 0), а = b = 6, уравнения асимптот: x = 0 и у = 0; 2) С (0; 0), а = b = 3, уравнения асимптот: x = 0 и у = 0, 3) С (0; 0), а = b = 5, уравнения асимптот: x = 0 и у = 0. 551. (6; 2) и (13/3, - 2/3).
552. (25/4; 3) - прямая касается гиперболы. 553. Прямая проходит вне гиперболы. 554. 1) Касается гиперболы; 2) пересекает гиперболу в двух точках; 3) проходит вне гиперболы. 555. 1) При |m| > 4,5 - пересекает гиперболу; 2) при m = ± 4,5 - касается гиперболы; 3) при |m| < 4,5-проходит вне гиперболы. 556. k2a2 - b2 - m2.
560. 10x - 3у - 32 = 0, 10x - 3у + 32 = 0; 561. x + 2y - 4 = 0, x + 2y + 4 = 0; d = 8√5/5. 562. M1 (-6; 3); d = 11/13√13. 563. 5x - 3y - 16 = 0; 13x + 5y + 48 = 0. 564, 2x + 5y -16 = 0.
565. d = 17/10√10. 566. x2/5 - y2/45 = 1, 3x /10 - 4y2/45 = 1.
567. x2/16 - y2/4 = 1. 568. x = -4, x = 4, y = -1 и y = 1.
572. x2/5 - y2/4 = 1. 573 x2/16 - y2/9 = 1.
575. 2x + 11у + 6 = 0. Указание. Воспользоваться свойством гиперболы, сформулированным в задаче 574. 577. x2 - y2 =16.
578. x2/16 - y2/9 = 1. 579. x2/25 - y2/4 = 1. 580. q = 2/3. 581. a = 2. 582. q1 = 2, q2 = 5/7. 583. 1) y2 = 6x; 2) y2 = -x; 3) x2 = 1/2y; 4) x2 = -6y
584. 1). p = 3; в правой полуплоскости симметрично оси Оx; 2) р = 2,5; в верхней полуплоскости симметрично оси Оу; 3) р = 2; в левой полуплоскости симметрично оси Оx; 4) р = 1/22; в нижней полуплоскости симме-
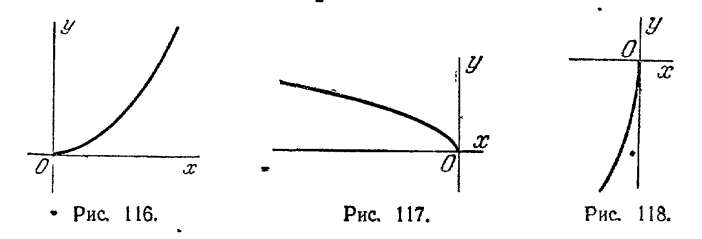
трично оси Оу. 585 1) у2 = 4x; 2) у2 = -9x; 3) x2 = у; 4) x2 = -2у. 586. 40 см. 587. x2 = - 12у.