Декартовы прямоугольные координаты в пространстве
Решение задачДекартова прямоугольная система координат в пространстве определяется заданием линейной единицы для измерения длин и трех пересекающихся в одной точке взаимно перпендикулярных осей, занумерованных в каком-либо порядке.
Точка пересечения осей называется началом координат, а сами оси - осями координат. Первая координатная ось называется осью абсцисс, вторая - осью ординат, третья - осью апликат.
Начало координат обозначается буквой О, оси координат обозначаются соответственно символами Ох, Оу, Оz.
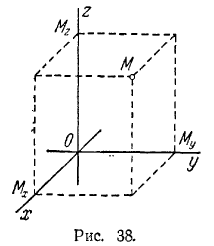
Пусть М - произвольная точка пространства, Mx, Мy и Mz - ее проекции на координатные оси (рис. 38).
Координатами точки М в заданной системе называются числа:
x = OMx, y = OMy, z = OMz
(рис. 38), где ОМx есть величина отрезка ОМx оси абсцисс, ОМy - величина отрезка ОМy оси ординат, ОМz - величина отрезка ОМz оси апликат. Число х называется абсциссой, у - ординатой, z - апликатой точки М. Символ М(х; у; z) обозначает, что точка М имеет координаты х, у, z.
Плоскость Оуz разделяет все пространство на два полупространства; то из них, которое расположено ь положительном направлении оси Ох, называется ближним, другое - дальним. Плоскость Охz также разделяет пространство на два полупространства; то из них, которое расположено в положительном направлении оси Оу, называется правым, другое - левым. Наконец, и плоскость Оху разделяет пространство на два полупространства; то из них, которое расположено в положительном направлении оси Оz, называется верхним, другое - нижним.
Три плоскости Оху, Охz и Оуz вместе разделяют пространство на восемь частей; их называют координатными октантами и нумеруют так, как показано на рис. 39.
719. Построить (в аксонометрической проекции) следующие точки по их декартовым координатам; A(3;4;6), В(-5; 3; 1), С( 1; -3; -5), D (0; -3; 5), Е(-3; -5; 0) и F(-1; -5; -3).
720. Найти координаты проекций точек A (4; 3; 5), B(-3; 2; 1), С(2; -3; 0) и D{0; 0; -3): 1) на плоскость Оху; 2) на плоскость - Oxz; 3) на плоскость Oyz; 4) на ось абсцисс; 5) на ось ординат; 6) на ось апликат.

721. Найти координаты точек, симметричных точкам A (2; 3; 1), В(5; -3; 2), С(-3; 2; -1) и D(a; b; с) относительно: 1) плоскости Оху; 2) плоскости Охz; 3) плоскости Oyz; 4) оси абсцисс; 5) оси ординат; 6) оси апликат; 7) начала координат.
722. Даны четыре вершины куба: A (-а; -а; -а), В{а; -а; -а); С(-а; а; -а) и D(a; а; а). Определить его остальные вершины.
723. В каких октантах могут быть расположены точ-ки, координаты которых удовлетворяют одному из сле-дующих условий: 1) x - y = 0; 2) х + у = 0; 3) х - z = 0; 4) х + z = 0; 5) у - z = 0; 6) у + z = 0.
724. В каких октантах могут быть расположены точки, если: 1) ху > 0; 2) xz < 0; 3) yz> 0; 4) xyz > 0; 5) xyz < 0.
725. Найти центр шара радиуса R = 3, который касается всех трех координатных плоскостей и расположен: 1) во втором октанте; 2) в пятом октанте; 3) в шестом октанте; 4) в седьмом октанте; 5) в восьмом октанте.