Центр линии второго порядка

Линия, которая в некоторой декартовой системе координат определяется уравнением второй степени, называется линией второго порядка. Общее уравнение второй степени (с двумя переменными) принято записывать в виде:

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0. (1)

Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами. Линии второго порядка, обладающие единственным центром, называются центральными.

Точка S(x₀; у₀) является центром линии, определяемой уравнением (1), в том и только в том случае, когда ее координаты удовлетворяют уравнениям:

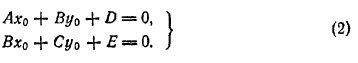
Обозначим через δ определитель этой системы:

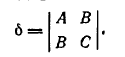
Величина δ составляется из коэффициентов при старших членах уравнения (1) и называется дискриминантом старших членов этого уравнения.

Если δ ≠ 0, то система (2) является совместной и определенной, т. е. имеет решение и притом единственное. В этом случае координаты центра могут быть определены по формулам:

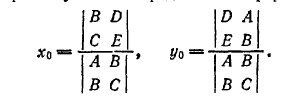
Неравенство δ ≠ 0 служит признаком центральной линии второго порядка

Если S(x₀; у₀) - центр линии второго порядка, то в результате преобразования координат по формулам

(что соответствует переносу начала координат в центр линии) ее уравнение примет вид

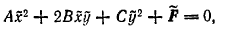
где А, В, С - те же, что в данном уравнении (1), a 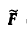определяется формулой

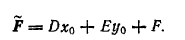
В случае δ ≠ 0 имеет место также следующая формула:

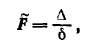
где

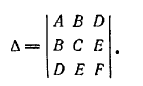
Определитель Δ называется дискриминантом левой части общего уравнения второй степени.

665. Установить, какие из следующих линий являются центральными (т. е. имеют единственный центр), какие не имеют центра, какие имеют бесконечно много центров:

1) 3x² - 4ху -2у² + Зх - 12у - 7 - 0;

2) 4x² + 5ху + 3у² - х + 9у - 12 = 0;

3) 4x² - 4ху + у² - 6x + 8y + 13 = 0;

4) 4x² - 4ху + у² - 12x + 6у - 11=0;

5) х² - 2ху + 4у² + 5х - 7у + 12 = 0;

6) x² - 2ху + у² - 6x + 6y - 3 = 0;

7) 4х² - 20ху -4- 25у² - 14x + 2у - 15 = 0;

8) 4х² - 6ху - 9у² + Зх - 7у + 12 = 0.

666. Установить, что следующие линии явпяются центральными, и для каждой из них найти координаты центра:

1) 3x² + 5ху + у² - 8x - 11у - 7 = 0;

2) 5x² + 4ху + 2у² + 20x + 20у - 18 = 0;

3) 9x² - 4xy - 7у² - 12 = 0;

4) 2x² - 6ху + 5у² + 22x - 36у + 11 = 0.

667. Установить, что каждая из следующих линий имеет бесконечно много центров; для каждой их них составить уравнение геометрического места центров:

1) х² -6ху + 9у² - 12x + 36y + 20 = 0;

2) 4x² + 4ху + у² - 8х - 4y - 21 = 0;

3) 25x² - 10xy + y² + 40x - 8y + 7 = 0.

668. Установить, что следующие уравнения определяют центральные линии; преобразовать каждое из них путем переноса начала координат в центр;

1) 3x² - 6ху + 2у² - 4x + 2y + 1 = 0;

2) 6х² + 4ху + у² + 4x - 2y + 2 - 0;

3) 4x² + 6xy + y² - 10x - 10 = 0;

4) 4x² + 2xy + 6y² + 6x - 10y + 9 = 0.

669. При каких значениях m и n уравнение

mx² + 12ху + 9y² + 4х + nу - 13 = 0

определяет:

1) центральную линию;

2) линию без центра;

3) линию, имеющую бесконечно много центров.

670. Дано уравнение линии 4x² - 4xy + у² + 6x + 1 = 0. Определить, при каких значениях углового коэффициента k прямая у = kx: 1) пересекает эту линию в одной точке; 2) касается этой линии; 3) пересекает эту линию в двух точках; 4) не имеет общих точек с этой линией.

671. Составить уравнение линии второго порядка, которая, имея центр в начале координат, проходит через точку M(6;-2) и касается прямой x - 2 = 0 в точке N(2; 0).

672. Точка Р (1; -2) является центром линии второго порядка, которая проходит через точку Q(0;-3) и касается оси Ох в начале координат. Составить уравнение этой линии.