Самосопряженные операторы и их матрицы

Определение 6.2. Линейный оператор А, действующий в евклидовом пространстве, называют самосопряженнымu, если А* = А.

Это определение можно сформулировать по-другому. Линейный оператор самосопряженный, если для любых векторов х и у верно равенство

(Ах,у) = (х, Ау).

Действительно, если указанное соотношение выполняется, то, согласно определению 6.1, линейный оператор А является сопряженным оператором к самому себе, т.е. А* = А.

Пример 6.3. Самосопряженными являются простейшие линейные операторы: нулевой Θ и тождественный I, так как для любых векторов х и у

(Iх, у) = (x, у) = (x, Iу), (Θx, у) = (0, у) = 0 = (x, 0) = (x, Θу).

Пример 6.4. Рассмотрим линейное пространство V₃ с обычным скалярным произведением свободных векторов (x, у). Отображение A: V₃ → V₃ ортогонального проектирования векторов из V₃ на направление вектора а единичной длины, которое определяется формулой Ах = (x, а) а, является линейным оператором, так как

А(μх + vу) = (μх + vy, а) а = μ(х, a)a + v(у, а)a = μ(Ах) + v(Ay).

Убедимся, что этот оператор является самосопряженным:

(Ах, у) = ((x,a)а, у) = (x, а) • (а, у) = (x, (a,у)а) = (x, (у,а)а) = (x, Ау).

Приведенные рассуждения не используют специфику пространства V₃ и могут быть проведены в произвольном евклидо-вом пространстве. Любой единичный вектор а евклидова пространства Ε порождает линейный оператор Р_a ортогонального проектирования на линейное подпространство Н = span{a} со-гласно формуле Р_aх = (x, а) а, и этот оператор является само-сопряженным.

Теорема 6.2. Матрица самосопряженного оператора в любом ортонормированном базисе является симметрической. Наоборот, если матрица линейного оператора в некотором ортонормированном базисе является симметрической, то этот оператор - самосопряженный.

◄ Согласно определению 6.2, А - самосопряженный оператор, если А = А*, т.е. если линейный оператор равен своему сопряженному оператору. Это эквивалентно тому, что матрица линейного оператора в ортонормированном базисе совпадает со своей транспонированной (она является матрицей сопряженного оператора). Такие матрицы и называют симметрическими. ►

Напомним, что комплексные числа а + bi и а - bi называют комплексно сопряженными. Число, комплексно сопряженное к числу z, обозначают z. Рассмотрим произвольную матрицу М = (m_ij), элементами которой являются комплексные (в частности, действительные) числа m_ij. Матрицу M = (m_ij) того же типа, что и М, элементами которой являются числа m_ij, будем называть комплексно сопряженной к матрице М. Она состоит из комплексно сопряженных элементов матрицы М: M - (m_ij). Из свойств комплексных чисел вытекают следующие соотношения:

M+N = M + N, MN = MN, M^T=(M)^T.

Теорема 6.3. Все корни характеристического уравнения самосопряженного оператора действительны.

◄ Согласно теореме 6.2, утверждение можно переформулировать следующим образом: характеристическое уравнение симметрической матрицы имеет только действительные корни. В этой форме и будем его доказывать.

Предположим, что некоторое число λ, вообще говоря комплексное, является корнем характеристического уравнения симметрической матрицы А, т.е. det (А - λЕ) = 0. Тогда система линейных алгебраических уравнений (А - λЕ)х = 0 имеет некоторое ненулевое решение х = (х₁ ... х_n)^T, состоящее из комплексных чисел x_k, k = 1,n. Рассмотрим столбец x, комплексно сопряженный к столбцу х. Умножим равенство (А - λЕ)х = 0 слева на строку x^T. Тогда

x^T (А - λЕ)х = 0,

или

x^T = λx^Tx . (6.5)

Так как произведение комплексного числа на сопряженное к нему является действительным числом, равным квадрату модуля комплексного числа, а x - ненулевое решение, то

x^Tx = x₁x₁ + ... + x_nx_n = |x₁|² + ... + |x_n|² > 0,

т.е. матричное произведение x^Tх представляет собой действительное положительное число.

Из равенства 6.5 находим

λ = x^TAx/x^Tx

причем знаменатель дроби справа является действительным числом. Следовательно, число λ будет действительным, если числитель этой дроби ω = x^TАх будет числом действительным.

В силу симметричности матрицы А

ω = ω^T = (x^TАх)^T = х^TА^Tx = х^TАx.

Поэтому с учетом свойств операции комплексного сопряжения матриц и благодаря тому, что элементами матрицы А являются действительные числа, получаем

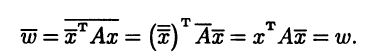
Комплексное число, сопряженное самому себе - это действительное число. Следовательно, и ω является действительным. ►

Следствие 6.1. Если матрица А является симметрической, то все корни ее характеристического уравнения det(A - λЕ) = 0 действительные.

Следствие 6.2. Самосопряженный оператор, действующий в n-мерном евклидовом пространстве, имеет n собственных значений, если каждое из них считать столько раз, какова его кратность.

Следствие 6.3. Симметрическая матрица порядка n имеет n собственных значений, если каждое из них считать столько раз, какова его кратность.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ