Сопряженный оператор

p>Пусть Ε - евклидово пространство.

Определение 6.1. Линейный оператор А*: Ε → Ε называют сопряженным к линейному оператору А: Ε → Ε, если для любых векторов x, у ∈ Ε верно равенство

(Ах, у) = (x, А*у). (6.1)

Данное определение сформулировано так, что оставляет открытыми два вопроса. Во-первых, не ясно, каждый ли линей-ный оператор, действующий в евклидовом пространстве, имеет сопряженный. Во-вторых, из определения нельзя понять, одно-значно или нет определяется сопряженный оператор. Прежде чем формулировать теорему, отвечающую на оба эти вопроса, докажем одно вспомогательное утверждение.

Лемма. Если квадратные матрицы М и N порядка n таковы, что для любых вектор-столбцов x,у ∈ Rⁿ выполняется соотношение х^TМу = x^TNy, то М = N.

◄ Пусть m_ij, n_ij - элементы матриц М и N соответственно, стоящие в i-й строке и j-м столбце. Для произвольной пары индексов i и j выберем такие вектор-столбцы х и у:

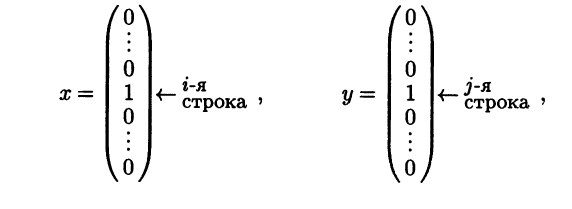
в которых присутствует только один ненулевой элемент, равный единице и стоящий на указанном месте. Записав равенство х^TМу = х^TNу с выбранными столбцами х и у и вычислив обе стороны равенства, получаем m_ij = n_ij

Так как пара индексов может быть выбрана произвольно, заключаем, что М = N. ►

Теорема 6.1. Любому линейному оператору А: Ε → Ε соответствует единственный сопряженный оператор А*, причем его матрицей в любом ортонормированием базисе е является матрица А^T, транспонированная матрице А линейного оператора А в том же базисе е.

◄ Доказательство теоремы основано на том, что фиксированный базис евклидова пространства Ε позволяет установить взаимно однозначное соответствие между линейными операторами из L{Ε,Ε) и матрицами из М_n(R), n = dimΕ. Это соответствие заключается в сопоставлении линейному оператору его матрицы в фиксированном базисе.

Докажем, что линейный оператор В с матрицей В = А^T в базисе е является сопряженным к линейному оператору А. Для этого достаточно проверить выполнение равенства

(Ах, у) = (х, By) (6.2)

для любой пары векторов х, у ∈ Ε.

Пусть х, у - столбцы координат векторов х, у в базисе е. Тогда, согласно теореме 4.3, вектор Ах имеет столбец координат Ах, а лев&л часть равенства (6.2) равна (Ах)^Tу, что следует из ортонормированности базиса (см. 3.7). Аналогично правая часть этого равенства имеет вид х^T(By). Следовательно, равенство (6.2) в координатной записи имеет вид

(Ах)^Tу = х^T(Ву). (6.3)

Так как (Аx)^T = х^TА^T в силу свойств матричных операций, равенство (6.3) эквивалентно равенству

х^TА^Tу = х^TBy, (6.4)

которое при В = А^T превращается в тождество.

Если некоторый линейный оператор В является сопряжен-ным к линейному оператору А, то для любых векторов х и у выполняется равенство (6.2). Значит, для матриц А и В этих операторов равенство (6.4) выполняется для любых столбцов х и у. Согласно доказанной лемме, В = А^T. Поэтому линейный оператор В определен однозначно, так как однозначно определена его матрица. ►

В некоторых случаях линейный оператор, сопряженный к данному линейному оператору, можно найти, не вычисляя матрицы этого оператора.

Пример 6.1. Вектор а ∈ V₃ порождает линейный оператор A: V₃ → V₃ согласно формуле

Ах = а × х.

Оператор, сопряженный к оператору А, можно определить, опираясь на свойства скалярного, векторного и смешанного произведений [III]:

(Ах, у) = (а×х, у) = аху = уах = (у×а, х) = (х, у×а) = (х, -а×у) = (х,-Ау).

Из приведенных соотношений видно, что А* = -А.

Пример 6.2. Множество С^∞₀[а, b] бесконечно дифференцируемых на отрезке [а, b] функций, у которых в точках а и b производные любого порядка равны нулю, является линейным пространством относительно обычных операций сложения функций и умножения функции на действительное число, а формула

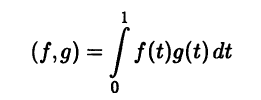
задает в этом линейном пространстве скалярное произведение (см. пример 3.4). Отображение Af = f', которое каждой функции f ∈ С^∞₀[а, b] ставит в соответствие ее производную, является линейным оператором. Оператором, сопряженным к А, будет -А, поскольку, согласно правилу интегрирования по частям,

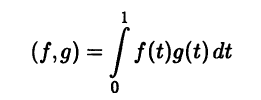
1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ