Характеристическое уравнение линейного оператора

Рассмотрим линейный оператор А: L → L, действующий в линейном пространстве L. Выберем в линейном пространстве L некоторый базис b и запишем в этом базисе матрицу А = (а_ij) линейного оператора А. Согласно следствию 4.3 матрица А - λЕ является матрицей линейного оператора А - λI, где I - тождественный оператор. Определитель det(А - λЕ) матрицы линейного оператора А - λI, согласно следствию 4.2, от выбора базиса не зависит. Значит, характеристический многочлен _χA(λ) матрицы А является также характеристическим многочленом любой другой матрицы оператора А и совпадает с определителем линейного оператора А - λI. Мы можем ввести следующее определение.

Определение 5.2. Характеристическим многочленом линейного оператора А: L → L называют характеристический многочлен его матрицы А, записанной в некотором базисе, а характеристическим уравнением этого оператора - характеристическое уравнение матрицы А.

Определение корректно, так как характеристический мно-гочлен не зависит от выбора базиса. При этом коэффициенты d_k характеристического многочлена, представленного в виде (5.1) , также не связаны с используемым базисом, т.е. являются инвариантами относительно выбора базиса. Другими словами, коэффициенты d_k отражают свойства самого оператора, а не его матрицы А, являющейся записью оператора в конкретном базисе.

Коэффициенты d_k могут быть выражены в виде многочленов от элементов матрицы оператора. Таким образом, хотя коэффициенты матрицы меняются при замене базиса, некото-рые выражения от этих коэффициентов остаются неизменными. Наиболее просто выражается коэффициент

d_n-1 = а₁₁ + a₂₂ + ... + а_nn,

равный сумме диагональных элементов матрицы А. Этот коэффициент называют следом линейного оператора А (следом матрицы А) и обозначают trA (trA) или spA (spA). Коэффициент d₀ характеристического многочлена совпадает со значением этого многочлена при λ = 0 и равен определителю линейного оператора А.

Пример 5.2. В линейном пространстве К₂[х] многочленов степени не выше двух элементы 1, х, х2 образуют базис. Матрица А линейного оператора дифференцирования в этом базисе имеет вид

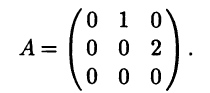
Вычислив определитель

и приравняв его нулю, получим характеристическое уравнение этого линейного оператора: λ³ = 0.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ