Линейные пространства линейных операторов
Теория- Автор
- Издательство
Обозначим через L(L,L') множество всех линейных операторов, действующих из линейного пространства L в линейное пространство L'. В этом множестве введем операции сложения линейных операторов и умножения линейного оператора на действительное число. Суммой линейных операторов А, В ∈ L(L,L') назовем оператор А + В ∈ L(L,L'), определяемый формулой
(А + В)х = Ах + Вх, х ∈ L,
а произведением линейного оператора А ∈ L(L,L') на действительное число λ назовем оператор λА ∈ L(L,L'), действующий согласно формуле
(λА)х = λ(Ах).
Поскольку
(А + В)(αх + βу) = A(αx + βy) + B(αx + βy) = (αАх + βАу) + (αВх + βBy) = α(Ах + Вх) + β(Ay + By) = α(А + В)х + β(А + В)у
и
(λА)(αх + βу) = λ(A(αx + βу)) = λ(А(αх) + А(βу)) = (λα)Аx + (λβ)Ау = (αλ) Ах + (βλ)Aу = α(λАх) + β(λАу) = α((λА)х) + β((λА)у),
отображения А + В и λA действительно являются линейными операторами. Таким образом, относительно введенных нами операций множество L(L,L') замкнуто. Проверив аксиомы линейного пространства, можно убедиться, что L(L,L') относительно этих операций является линейным пространством.
Для каждого линейного оператора А: L → L' определен линейный оператор (-А), задаваемый равенством (-А)х - = -(Ах). Нетрудно проверить, что (-А) действительно линейный оператор:
(-А)(λx + μу) = -(A(λx + μу)) = -(λ Ах + μАу) = λ(-(Ах)) + μ(-(Ау)) = λ((-А)х) + μ((-А)у).
В сумме с А линейный оператор (-А) дает нулевой оператор. Поэтому в соответствии с терминологией линейных пространств (-А) называют оператором, противоположным к А.
Линейное пространство L(L,L) линейных операторов из линейного пространства L в себя называют линейным про-странством линейных операторов (преобразований) пространства L.
Каждому линейному оператору А ∈ L(L,L), действующему в n-мерном линейном пространстве L, в заданном базисе b соответствует квадратная матрица А порядка n (матрица этого линейного оператора). Тем самым определено отображение Ф: L(L,L) → Мn(R) из линейного пространства L(L,L) в линейное пространство Мn(R) квадратных матриц порядка n с действительными коэффициентами, при этом Ф(A) = А. Согласно теореме 4.4 отображение Ф является биективным.
Теорема 4.10. Пусть в n-мерном линейном пространстве L задан некоторый базис b. Тогда отображение Ф: L(L,L) → Мn(R), сопоставляющее каждому линейному оператору его матрицу в базисе b, является изоморфизмом линейных пространств L(L,L) и Мn(R).
◄ Как мы уже отметили, отображение Ф биективно, и нам остается показать, что оно линейно. Пусть А и В - два произвольных линейных оператора из линейного пространства L(L,L). Тогда для любого вектора х ∈ L, со столбцом координат х
(А + В)х = Ах + Вх = bАх + bВх = b((A + В)х),
где А и В - матрицы операторов А и В в базисе b. Итак, действие линейного оператора А + В в базисе b записывается как умножение столбца координат вектора слева на матрицу А + В. Значит, А + В и является матрицей линейного оператора А + В.
Итак, сложению линейных операторов при отображении Ф соответствует сложение их матриц. Аналогично умножению линейного оператора на действительное число λ соответствует умножение его матрицы на это число:
(λА)х = λ(Аx) = λ(bАх) = b((λА)х).
Условия а), б) определения 4.1 выполнены, поэтому отображение Ф линейно ►
Следствие 4.3. Бели матрицы А,В ∈ Мn(R) являются матрицами линейных операторов А, В ∈ L(L, L) в некотором базисе b линейного пространства L, то для любых чисел λ и μ матрица λА + μВ является матрицей линейного оператора λА + μВ ∈ L(L,L) в том же базисе b.
◄ Эта формулировка лишь перефразирует утверждение, что отображение Ф: L(L,L) → Мn(R) является линейным, что доказано в теореме 4.10. ►
Вопросы и задачи
- Выясните, являются ли линейными следующие отображения пространства V3: а) x → 3(x,x)x; б) ортогональная проекция на плоскость хОу; в) x → (x × a) × b, где а, b - фиксированные векторы пространства V3.
- Выясните, являются ли линейными следующие отображения линейного пространства всех многочленов от переменной t в себя:
- Будет ли линейным отображение A: R3 → R3, если: а) А(x) = (sinx1, 0, x3); б) А(x) = (х1 + x3, 2x2 + x3, - x1), где x = (x1, x2, x3).
- Покажите, что линейным оператором является отображение А, которое каждый вектор x = α1e1 + ... + αnen, заданный в линейном пространстве L своими координатами от-носительно базиса е = (e1 ... еn), отображает в вектор А(x) = α1e1 + ... + αmem, где m < n (оператор проектирования на подпространство span{e1,...,еm}). Найдите матрицу этого ли-нейного оператора в базисе е.
- Запишите в заданном базисе матрицу следующих линейных операторов, действующих в линейном пространстве V3:
- В пространстве V3 задан вектор с = 3i - 2j + k. Докажите, что отображение А, определяемое условием А(x) = с × x, является линейным. Найдите его матрицу в базисе i, j, k.
- В линейном пространстве Кn[х] многочленов перемен-ного х степени не выше n задан линейный оператор дифферен-цирования D [Р(x)] = Р'(х). Запишите матрицу этого оператора в базисе
- Пусть L и L' - линейные пространства. Какому линейному пространству изоморфно пространство L(L,L')? Чему равна размерность пространства L(L,L')?
- Определите, какие из следующих отображений A: R3 → R3 являются линейными:
- Рассмотрим линейное пространство всех матриц второго порядка. Покажите, что умножение справа любой матрицы этого пространства на матрицу
- Покажите, что в линейном арифметическом пространстве R3 существует единственный линейный оператор, переводящий векторы a1, а2, а3 соответственно в векторы b1, b2, b3,и найдите матрицу этого оператора в том же базисе, в котором даны координаты указанных векторов:
- Линейный оператор А в базисе (е1 е2 е3 е4) имеет матрицу
- Как изменится матрица линейного оператора, если в базисе (e1 ... еn) поменять местами два вектора еi и ej?
- Линейный оператор А в базисе (e1 е2 е3) имеет матрицу
- Линейный оператор A ∈ L(R3,R3) в базисе
- Найдите матрицу линейного оператора дифференци-рования, действующего в линейном пространстве многочленов степени не выше двух, в базисе е1 = 1, е2 = х, е3 = x2. Используя матрицу перехода, найдите матрицу этого оператора в базисе f1 = 1, f2 = x - 1, f3 = (х - 1)2/2.
а) умножение многочлена на t;
б) умножение многочлена на t2;
в) дифференцирование многочлена.
а) оператора проектирования на плоскость хОу, базис i, j, k;
б) оператора проектирования на ось Оу, базис i, j, k;
в) оператора проектирования на плоскость хОу, базис е1 = i, е2 = j, е3 = i + j + k.
e1 = 1, e2 = x, e3 = x2/2!, ... , en = xn/n!.
а) А(х) = (x1 + 1, x2, x3 + 3);
б) А(х) = (x21, 2x2 + x3, x1 - x2);
в) А(х) = (x1 - x2 + х3, x3, x2);
г) А(х) = (x2 + x3, x1 + x3, 3x1 - x2 + х3),
если x = ( х1, x2, x3). Для линейных операторов найти матрицы в базисе, в котором заданы векторы х и А(х).
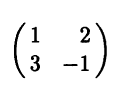
есть линейный оператор. Найдите матрицу этого оператора в базисе
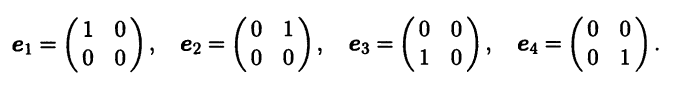
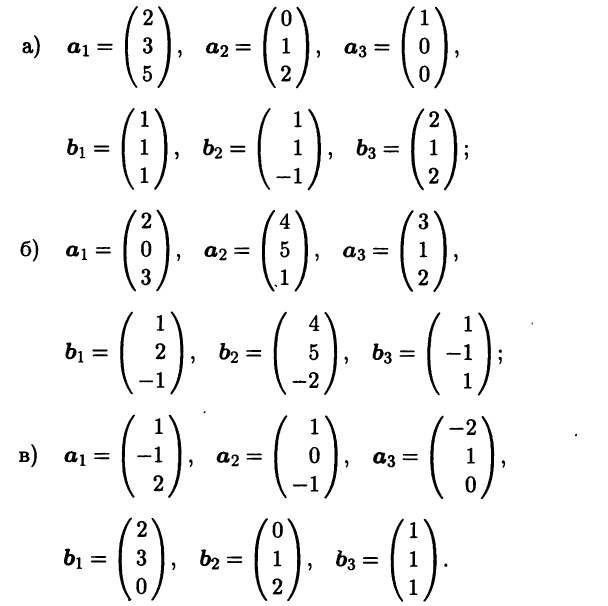
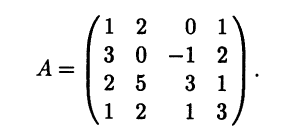
Найдите матрицу этого оператора в базисе:
а) e4, е2, е3, е1;
б) f1 = е1, f2 = е1 + е2, f3 = е1 + е2 + е3, f4 = е1 + е2 + е3 + е4;
в) f1 = е1 - е2, f2 = е1 - е3, f3 = е1 - e4, f4 = e4.
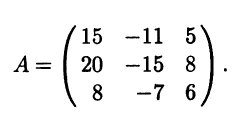
Найдите матрицу этого оператора в базисе f1 = 2e1 + 3е2 + е3, f2 = 3е1 + 4е2 + е3, f3 = е1 + 2е2 + 2е3.
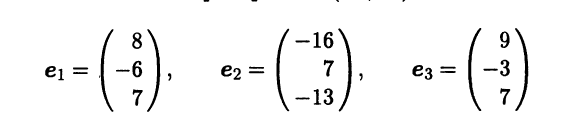
имеет матрицу
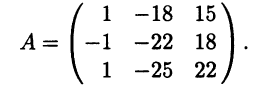
Найдите матрицу этого оператора в базисе
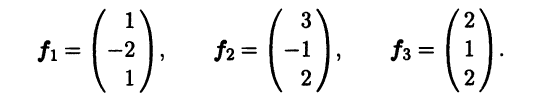
Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ