Преобразование матрицы линейного оператора

Матрица линейного оператора изменяется, когда изменяется базис линейного пространства. Возникает естественный вопрос, как она изменяется. Напомним, что связь двух базисов, старого (исходного) и нового, отражается матрицей перехода.

Теорема 4.6. Матрицы А_b и А_e линейного оператора А: L → L, записанные в базисах b и е линейного пространства L, связаны друг с другом соотношением

А_e = U^-1A_bU, (4.2)

где U = U_b→e - матрица перехода от базиса b к базису е.

◄ Пусть у = Ах. Обозначим координаты векторов х и у в старом базисе b через х_b и у_b, а в новом базисе е - через х_e и у_e. Поскольку действие линейного оператора А в матричной форме в базисе b имеет вид у_b = А_bх_b (см. теорему 4.3), а координаты векторов х и у в новом и старом базисах связаны между собой равенствами (см. 1.8)

x_b = Ux_e, y_b = Uy_e,

то получаем

y_e = U^-1_b = U^-1(A_bx_b) = U^-1(A_bUx_e) = (U^-1A_bU)х_e .

Равенство у_e = (U^-1A_bU) х_e является матричной формой записи действия линейного оператора А в базисе е и поэтому, согласно теореме 4.4, U^-1A_bU = А_e.

Изложенное доказательство теоремы хорошо иллюстрирует следующая диаграмма:

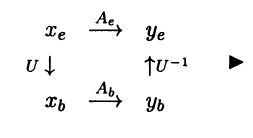
Определение 4.5. Квадратные матрицы А и В порядка n называют подобными, если существует такая невырожденная матрица Р, что Р^-1АР = В.

Формула (4.2) означает, что матрицы, представляющие один и тот же линейный оператор в разных базисах, являются подобными. Верно также и обратное: если две матрицы А и В подобны, т.е. В = Р^-1AР, то их можно рассматривать как матрицы одного оператора, но в разных базисах. Дей-ствительно, в произвольном п-мерном линейном пространстве зафиксируем произвольный базис Ь и выберем линейный оператор, который в этом базисе имеет матрицу А. Тогда в базисе е = bР этот же оператор будет иметь матрицу Р^-1АР = В.

Теорема 4.7. Если матрицы А и В подобны, то detА = detВ.

◄ Если матрицы А и В подобны, то, согласно определению 4.5, существует такая невырожденная матрица Р, что В = Р^-1АР. Так как определитель произведения квадратных матриц равен произведению определителей этих матриц, a det(P^-1) = (detP)^-1 [III], то получаем

detB = det (P^-1AP) = det(P^-1) detA detP = detA. ►

Следствие 4.2. Определитель матрицы линейного оператора не зависит от выбора базиса.

◄ Действительно, возьмем матрицы А_b и А_e линейного оператора А в двух различных базисах b и е. Согласно теореме 4.6 и определению 4.5 эти матрицы подобны. Поэтому det А_b = det А_e по теореме 4.7. ►

Следствие говорит о том, что, хотя матрица линейного опе-ратора и изменяется при замене базиса, определитель ее при этом остается неизменным. Значит, этот определитель ха-рактеризует не конкретную матрицу оператора в конкретном базисе, а сам оператор. Это позволяет ввести следующее понятие.

Определение 4.6. Определителем линейного оператора называют определитель его матрицы в каком-либо базисе.

Пример 4.10. Линейный оператор A: V₃ → V₃, определяемый формулой Ах = x × i, в базисе i, j, k имеет матрицу

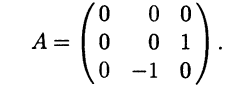
(см. пример 4.9). Определитель этой матрицы равен нулю. Значит, и в любом другом базисе определитель матрицы этого линейного оператора равен нулю.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ