Вычисления в ортонормированном базисе

Использование ортонормированных базисов облегчает вычисление скалярного произведения по координатам векторов. Пусть в евклидовом пространстве Ε задан некоторый базис е = (e₁ ... е_n). Рассмотрим два произвольных вектора х и у в этом пространстве. Эти векторы представляются в базисе е своими координатами:

х = x₁e₁ + ... + х_nе_n, у = y₁e₁ + ... + y_ne_n.

Запишем эти разложения векторов по базису в матричной форме:

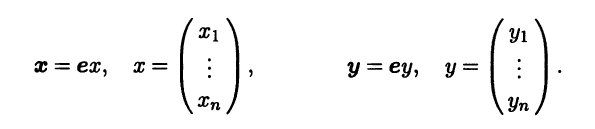
Скалярное произведение векторов х и у может быть выражено через скалярные произведения векторов базиса:

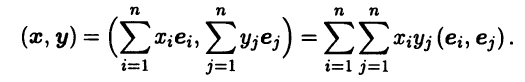
Составив из скалярных произведений базисных векторов ква-дратную матрицу Г = ((e_i,e_j)) порядка n, мы можем записать скалярное произведение заданных векторов в матричной форме:

(x,y) = x^TГy.

Матрица Г является симметрической в силу коммутативности операции скалярного умножения. Ее называют матрицей Грама системы векторов e₁, ..., е_n.

Пусть базис е является ортонормированным. Тогда скалярное произведение (е_i, е_j) при несовпадающих i и j равно нулю, а скалярные квадраты базисных векторов равны e²_i = ||е_i||² = 1. Это значит, что для ортонормированного базиса матрица Г является единичной. Поэтому

(x, у) = х^TЕу = x^Tу = x₁y₁ + x₂y₂ + ... + x_nу_n.

В частности, в ортонормированием базисе норма вектора х, которая выражается через скалярный квадрат этого вектора, может быть вычислена по формуле

||x|| = √(х,х) = √(х²₁ + ... + х²_n) = √(x^Tx), (3.7)

а для косинуса угла φ между ненулевыми векторами х и у получаем выражение

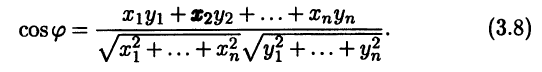
В ортонормированном базисе e₁, ..., е_n также упрощается вычисление координат вектора: они выражаются через скалярные произведения. Бели х = x₁e₁ + ... + х_nе_n, то, умножив равенство скалярно на вектор е_i, находим, что

(х, е_i) = x_i, i = 1,n.

Пример 3.13. В евклидовом арифметическом пространстве R⁴ найдем угол между векторами а = (-1, 1, 0, 2) и b = (2, -1, 1, 0). Согласно формуле (3.8),

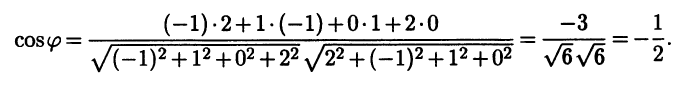
1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ