Ортогональные системы векторов

Определение 3.5. Два вектора в евклидовом пространстве называют ортогональными, если их скалярное произведение равно нулю.

Ортогональность векторов х и у будем обозначать так: х ⊥ у. Отметим, что, согласно свойству 3.3 скалярного умножения, нулевой вектор ортогонален любому другому.

Евклидово пространство - это, согласно определению 3.1 частный случай линейного пространства, и поэтому можно говорить о его линейных подпространствах в смысле определения 2.1. Каждое из таких линейных подпространств является евклидовым пространством относительно скалярного умножения, заданного в объемлющем евклидовом пространстве.

Говорят, что вектор х в евклидовом пространстве Ε ортогонален подпространству H, и обозначают х ⊥ H,, если он ортогонален каждому вектору этого подпространства.

Если H = span{a₁,...,а_k}, то условие х ⊥ H равносильно тому, что вектор х ортогонален каждому вектору a₁,..., а_k. Действительно, если х ортогонален H, то, согласно определению, он ортогонален и каждому вектору a₁,..., а_k. Докажем противоположное утверждение. Пусть х ⊥ a_i i = 1,k, и y ∈ H. Тогда вектор у является линейной комбинацией векторов а_i:

y = α₁a₁ + ... + α_ka_k,

и поэтому, согласно свойству 3.4,

(x,y) = α₁(x, a₁)+ ... + α_k(x, a_k) = 0.

В частности, если векторы х и а ортогональны, то для любого λ ∈ R векторы х и λа тоже ортогональны:

(x, λа) = λ(x, а) = 0.

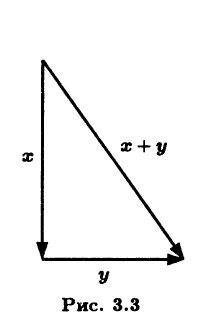
В пространстве V₃ ненулевым ортогональным векторам х и у можно сопоставить катеты прямоугольного треугольника, причем так, что их сумме, построенной по правилу треугольника, будет соответствовать гипотенуза этого прямоугольного треугольника (рис. 3.3). По аналогии с V₃ мы назовем в евклидовом пространстве сумму х + у ортогональных векторов х и у гипотенузой треугольника, построенного на х и у. Тогда на произвольное евклидово пространство распространяется известная теорема Пифагора.

Теорема 3.3. Если векторы ж и у из евклидова простран-ства ортогональны, то

||x + y||² = ||x²|| + ||y²||

◄ Здесь под нормой мы, как обычно, понимаем евклидову норму. Выразим левую часть этого равенства через скалярное произведение и воспользуемся условием ортогональности (x,у) = 0:

||x + y||² = (x + y, x + y) = (x,x) + 2(x,y) + (y, y) = ||x²|| + ||y²|| ►

Определение 3.6. Систему векторов евклидова пространства называют ортогональной, если любые два вектора из этой системы ортогональны.

Следующее свойство ортогональной системы является самым важным.

Теорема 3.4. Любая ортогональная система ненулевых векторов линейно независима.

◄ Рассмотрим произвольную ортогональную систему ненулевых векторов e₁, ..., е_m. Предположим, что для некоторых действительных коэффициентов α₁,..., α_m выполняется равенство

α₁e₁ +... + α_me_m = 0. (3.5)

Умножим это равенство скалярно на какой-либо вектор е_i:

(α₁e₁ +... + α_ie_i + ... + а_mе_m, е_i) = (0, е_i).

В силу свойства 3.3 скалярного произведения правая часть полученного равенства равна нулю, и мы, преобразуя левую часть в соответствии со свойством 3.4, получаем

α₁(e₁,e_i +...+ α_i(е_i, е_i) +... + α_m(e₁, е_i) = 0.

Так как система векторов ортогональна, то все слагаемые слева, кроме одного, равны нулю, т.е.

α_i(е_i, е_i) = 0. (3.6)

Так как вектор е{ ненулевой, то (ei, в{) Ф 0 (аксиома г) скалярного умножения). Поэтому из (3.6) следует, что = 0. Индекс г можно было выбирать произвольно, так что на самом деле все коэффициенты ai являются нулевыми. Мы доказали, что равенство (3.5) возможно лишь при нулевых коэффициентах, а это, согласно определению 1.2, означает, что система векторов ех, ..., ет линейно независима. ►

Пример 3.10. В евклидовом пространстве C[0, π] система функций coskx, k = 1,n, является ортогональной, поскольку

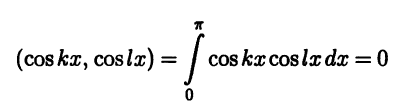
при k,l = 1,n, k ≠ l

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ