Нормированные пространства

В линейном пространстве обобщением понятия длины свободного вектора является норма. Длину вектора в линейном пространстве V₃ или V₂ можно рассматривать как функцию, определенную на множестве V₃ (соответственно V₂), которая каждому вектору ставит в соответствие число - его длину. Эта функция обладает некоторыми характерными свойствами [III], которые и служат основой для определения нормы в линейном пространстве. Норму вектора в линейном пространстве иногда называют длиной, имея в виду связь с аналогичным термином векторной алгебры.

Определение 3.2. Функцию, заданную на линейном пространстве L, которая каждому вектору х ∈ L ставит в соответ-ствие действительное число ||x||, называют нормой, если она удовлетворяет следующим аксиомам нормы:

а) ||х|| ≥ 0, причем равенство ||х|| = 0 возможно только при х = 0;

б) ||λх|| = |λ|||х||, λ ∈ R;

в) ||x + y|| ≤ ||х|| + ||у|| (неравенство треугольника).

Определение 3.3. Линейное пространство, в котором задана норма, называют нормированным пространством.

Евклидовы пространства и нормированные пространства представляют собой примеры линейных пространств с дополнительными структурами: скалярным умножением и нормой соответственно. Эти два понятия совершенно различны, однако, как утверждает следующая теорема, исходя из скалярного умножения в евклидовом пространстве можно задать норму и тем самым превратить евклидово пространство в нормированное.

Теорема 3.2. Всякое скалярное умножение в евклидовом пространстве определяет норму согласно формуле

||х|| = √(x,x) (3.3)

◄ Отметим, что, согласно аксиоме г) скалярного умножения, (х, х) ≥ 0 и, следовательно, функция, заданная соотношением (3.3), определена для всех векторов х евклидова пространства. Проверим выполнение аксиом нормы. Аксиома а) нормы немедленно следует из аксиомы г) скалярного умножения (определение 3.1). Аксиома б) нормы вытекает из аксиомы в) скалярного умножения и свойства 3.1:

||λх|| = √(λх, λх) = √(λ²(х, х)) = √λ² √(х,х) = |λ|||х||.

Остается проверить аксиому в) нормы, для чего мы воспользуемся неравенством Коши - Буняковского (3.1), которое можно записать в виде

(х, у) ≤ √(х,х)√(у, у)

или, с учетом (3.3),

(х,у) ≤ ||х|| ||у||.

Используя это неравенство, получаем

||х + у||² = (х + у,х + у) = (х, х) + 2(х,у) + (у, у) ≤ (х, х) + 2||х|| ||у|| + (у, у) = (||х|| + ||у||)². ►

Введение нормы по формуле (3.3) опирается только на общие свойства скалярного умножения, вытекающие из его аксиом, и не связано со спецификой конкретного линейного пространства. Поэтому такую норму в евклидовом пространстве называют евклидовой или сферической нормой. Когда говорят, не уточняя, о норме в евклидовом пространстве, обычно имеют в виду именно эту норму.

Вовсе не обязательно, чтобы в евклидовом пространстве норма вводилась через скалярное произведение. Рассмотрим следующие примеры, показывающие другие часто используе-мые нормы, не связанные с каким-либо скалярным произведением.

Пример 3.6. В линейном арифметическом пространстве Rⁿ нормой является функция ||•||₁ вида

||x||₁ = |x₁| + ... + |x_n|, x = (x₁, ..., x_n)

(|•| в правой части обозначает модуль действительного числа).

Легко убедиться, что аксиома а) нормы выполнена, так как величина |x₁| + ... + |х_n| всегда неотрицательна, причем она равна нулю тогда и только тогда, когда все компоненты x_i арифметического вектора равны нулю.

Так же просто убедиться в верности аксиомы б) нормы. Для проверки неравенства треугольника (аксиома в) нормы) выберем произвольные два вектора х = (x₁, ..., х_n) и у = (y₁,... ,y_n) из Rⁿ. Тогда

||x + y||₁ = ||(x₁ + y₁, ... , x_n + y_n)||₁ = |x₁ + y₁| + ... + |x_n + у_n| ≤ |x₁| + |y₁| + ... + |x_n| + |y_n| = ||x||₁ + ||y||₁.

Приведенную норму называют l₁ - нормой или октаэдрической нормой.

Пример 3.7. Функция

||x||∞ = max{|x₁|,...,|x_n| }

заданная на векторах х = (х₁, ..., х_n) в Rⁿ, также является нормой в Rⁿ. Эту норму называют l∞ - нормой или кубической нормой.

Как и в предыдущем примере проверка аксиом а) и б) нормы очевидна. Проверим неравенство треугольника для произвольных векторов х - ( х₁, ... , x_n) и у = (у₁, ..., у_n):

||x + y||∞ = ||(x₁ + y₁, ... ,x_n + y_n )||∞ = max{|x₁ + y₁|,...,|x_n + y_n|} ≤ 1| + |y₁|,...,|x_n| + |y_n|} ≤ mах{|x₁|,...,|х_n|} + max{|y₁|,...,|y_n|} = ||x||∞ - ||y||∞. #

Нормы ||x||, ||x||∞, ||x||₁ одного и того же вектора х связаны неравенствами

||x||∞ ≤ ||x|| ≤ ||x||₁,

которые непосредственно вытекают из определений этих норм.

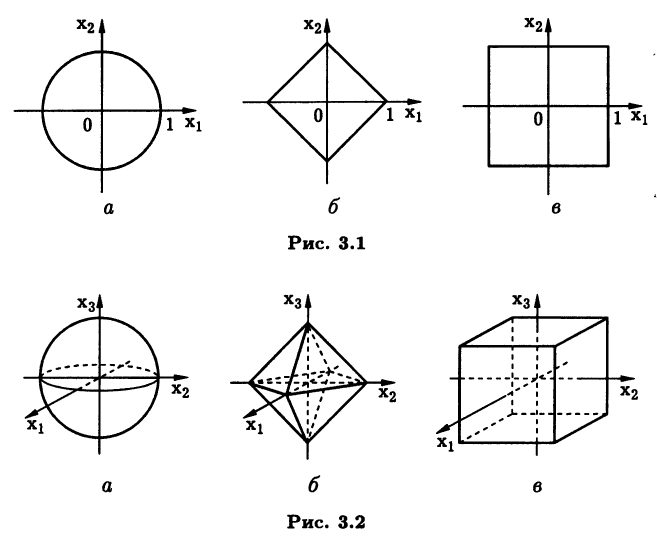
Пример 3.8. Множество S тех векторов х нормированного пространства, которые удовлетворяют равенству ||x|| = 1 (единичных векторов), называют единичной сферой. Множество S зависит от линейного пространства и однозначно определяет рассматриваемую в нем норму. На рис. 3.1 изображен вид единичной сферы для различных норм двумерного линейного пространства (конкретно линейного пространства радиус-векторов точек плоскости): евклидовой (рис. 3.1, а), октаэдрической (рис. 3.1,6) и кубической (рис. 3.1, в). В случае трехмерного линейного пространства (линейного пространства радиус-векторов) единичные сферы указанных норм изображе-ны на рис. 3.2. Мы видим, что это сфера (рис. 3.2, а), октаэдр (рис. 3.2, б) и куб (рис. 3.2, в). Вид единичной сферы для этих норм и послужил источником для их названий

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ