Неравенство Коши - Буняковского
Теория- Автор
- Издательство
Теорема 3.1. Для любых векторов х, у евклидова пространства Ε справедливо неравенство Коши - Буняковского
(x, y)2 ≤ (x, x) (у, y). (3.1)
◄ При x = 0 обе части неравенства (3.1) равны нулю согласно свойству 3.3, значит, неравенство выполняется. Отбрасывая этот очевидный случай, будем считать, что х ≠ 0. Для любого действительного числа λ, в силу аксиомы г), выполняется неравенство
(λx - у, λx - у) ≥ 0. (3.2)
Преобразуем левую часть неравенства, используя аксиомы и свойства скалярного умножения:
(λx - у, λx - у) = λ(x, λx - у) - (у, λx - у) = λ2 (x, x) - 2λ(x, у) + (у, у).
Мы получили квадратный трехчлен относительно параметра λ (коэффициент (x, x) при λ2 согласно аксиоме г) ненулевой, так как x ≠ 0), неотрицательный при всех действительных значениях параметра. Следовательно, его дискриминант равен нулю или отрицательный, т.е.
(x, у)2 - (x, x) (у, у) ≤ 0. ►
Пример 3.5. Доказательство неравенства Коши - Буняковского выглядит достаточно просто. Тем не менее это неравенство очень полезное. Применяя его в конкретных евклидовых пространствах, мы получаем некоторые хорошо известные в анализе и алгебре неравенства.
В случае линейного арифметического пространства Rn не-равенство Коши - Буняковского трансформируется в неравенство Коши
(a1b1 + ... + anbn)2 ≤ (а21 +... + a2n)(b21 +... + b2n).
В евклидовом пространстве С[0,1], скалярное произведение в котором выражается определенным интегралом (см. пример 3.4), неравенство Коши - Буняковского превращается в неравенство Буняковского (называемое также неравенством Шварца):
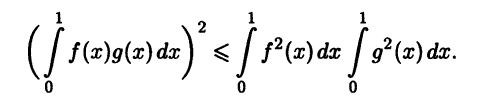
Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ