Прямое дополнение
Теория- Автор
- Издательство
Определение 2.6. Если линейные подпространства H1 и Н2 в линейном пространстве L образуют прямую сумму, причем Н1 ⊕ Н2 = L, то говорят, что Н1 является прямым дополнением для Н2.
Если линейное подпространство Н2 является прямым дополнением для линейного подпространства H1, то верно и обратное: Н1 является прямым дополнением для Н2. Оказывается, что любое линейное подпространство имеет прямое дополнение.
Теорема 2.7. Любое линейное подпространство Н в линейном пространстве L имеет прямое дополнение.
◄ Если линейное подпространство Н совпадает со всем линейным пространством L, то в качестве его прямого дополнения следует взять другое несобственное подпространство: Н1 = {0}. Точно так же прямым дополнением к нулевому подпространству {0} является само линейное пространство L. Опуская эти два тривиальных случая, полагаем, что линейное подпространство Н является собственным.
Выберем в Н какой-либо базис е = (e1 ... еk) и дополним его (см. замечание 2.1) системой векторов f = (f1 ... fm) до базиса (е f) в L. Положим H1 = span{f}. Тогда H + H1 = L, так как сумма H + H1 содержит все векторы системы (е f), являющейся базисом в L, а значит, и любой другой вектор линейного пространства. Остается доказать, что сумма Н + Н1 является прямой.
Выберем произвольный вектор у ∈ Н ∩ Н1. Тогда, с одной стороны, у = α1e1 + ... + αkek, так как у принадлежит линейному подпространству H, а с другой стороны, у = β1f1 + ... + βmfm так как у принадлежит линейному подпространству Н1. Эти две линейные комбинации есть два разложения вектора в базисе (е f) линейного пространства L и, следовательно, должны совпадать:
α1e1 + ... + αkek = β1f1 + ... + βmfm
или
alpha;1e1 + ... + αkek - β1f1 - ... - βmfm = 0.
Система векторов (е f) линейно независима, так как является базисом. Поэтому из последнего равенства векторов следует, что в нем все коэффициенты нулевые. Значит, вектор у является нулевым, а так как он выбирался произвольно, то Н ∩ Н1 = {0}. Поэтому линейные подпространства Н и Н1 образуют прямую сумму (см. теорему 2.3). ►
Вопросы и задачи
- Может ли линейное подпространство состоять из: а) двух элементов; б) одного элемента; г) 100 элементов?
- Может ли линейное подпространство конечномерного линейного пространства быть бесконечномерным?
- Докажите, что бесконечномерное линейное простран-ство содержит собственные бесконечномерные линейные подпространства.
- По аналогии с суммой двух линейных подпространств определите сумму конечного числа линейных одпространств.
- Пусть для линейных подпространств H1 и Н2 некоторого линейного пространства L выполняется равенство dim(H1 + Н2) = dimH1 + dimH2. Что можно утверждать о линейном пространстве: a) Н1 ∩ Н2, б) H1 + Н2?
- Найдите максимальное число линейно независимых векторов в системе векторов, заданных своими координатами
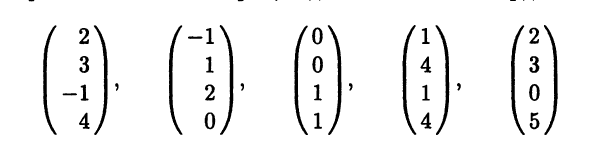 в некотором базисе линейного пространства £ размерности 4.
в некотором базисе линейного пространства £ размерности 4. - Докажите, что линейным подпространством является множество всех векторов n-мерного линейного арифметического пространства, удовлетворяющих условию:
- 2.8. Найдите размерность и базис линейной оболочки следующих векторов из R4:
- В линейном пространстве L, dimL = 4, две системы векторов е = (e1 е2 е3) и f = (f1 f2 f3) заданы своими координатами в некотором базисе:
- Найдите размерность и базис линейного подпространства в R4, состоящего из решений системы
- Докажите, что в линейном пространстве квадратных матриц порядка n линейные подпространства симметрических и кососимметрических матриц можно рассматривать как прямые дополнения друг друга.
- В линейном пространстве квадратных матриц порядка n найдите размерность и базис пересечения линейных подпространств верхних треугольных и нижних треугольных матриц.
- Докажите, что множество трехдиагональных матриц порядка n является линейным пространством относительно линейных матричных операций. Найти размерность и базис этого линейного пространства.
- В шестимерном линейном пространстве L даны два линейных подпространства H1 и H2 размерностей 3 и 4 соответственно. Что можно утверждать о размерности пересечения этих линейных подпространств? При выполнении какого условия справедливо равенство Н1 + H2 = L? Может ли сумма Н1 + H2 быть прямой?
- Сколько прямых дополнений имеет двумерное линейное подпространство в трехмерном линейном пространстве?
а) первые две координаты равны между собой;
б) первая координата равна нулю;
в) координаты удовлетворяют уравнению x1 + 2x2 + 22x3 + ... + 2n-1хn = 0.
Найдите базис и размерность этого линейного подпространства.
a1 = (1, -1, 1, 1), a2 = (2, 3, 1, 2), a3 = (4, 1, 3, 4).
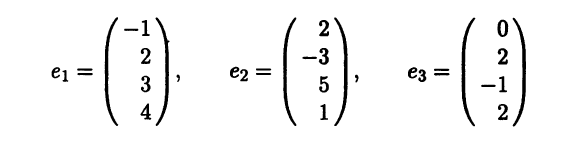
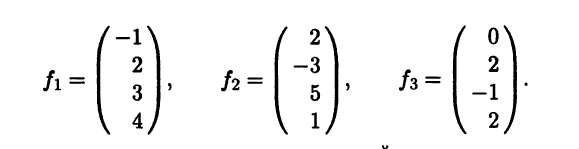
Какова размерность пересечения линейных подпространств span{e} и span{f}?
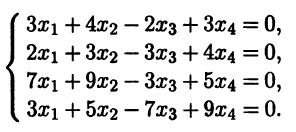
Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ