Определение и примеры

В любом линейном пространстве L можно выделить такое подмножество векторов, которое относительно операций из L само является линейным пространством. Это можно делать различными способами, и структура таких подмножеств несет важную информацию о самом линейном пространстве L.

Определение 2.1. Подмножество H линейного пространства L называют линейным подпространством, если выполнены следующие два условия:

1) сумма любых двух векторов из H принадлежит Н: x,y ∈ H ⇒ х + у ∈ Н;

2) произведение любого вектора из H на любое действительное число снова принадлежит Н: х ∈ Н, λ ∈ R ⇒ λж ∈ H.

Определение 2.1 фактически говорит о том, что линейное подпространство - это любое подмножество данного линейного пространства, замкнутое относительно линейных операций, т.е. применение линейных операций к векторам, принадлежащим этому подмножеству, не выводит результат за пределы подмножества. Покажем, что линейное подпространство Н как самостоятельный объект является линейным пространством относительно операций, заданных в объемлющем линейном пространстве L. В самом деле, эти операции определены для любых элементов множества L, а значит, и для элементов подмножества H. Определение 2.1 фактически требует, чтобы для элементов из H результат выполнения операций также принадлежал H. Поэтому операции, заданные в L, можно рассматривать как операции и на более узком множестве H. Для этих операций на множестве H аксиомы линейного пространства а)-б) и д)-з) выполнены в сцлу того, что они справедливы в L. Кроме того, выполнены и две оставшиеся аксиомы, поскольку, согласно определению 2.1, если x ∈ H то: 1) 0 • x = 0 ∈ H и 0 - нулевой вектор в Н; 2) (-1)х = -х ∈ H.

В любом линейном пространстве L всегда имеются два линейных подпространства: само линейное пространство L и нулевое подпространство {0}, состоящее из единственного элемента 0. Эти линейные подпространства называют несобственными, в то время как все остальные линейные подпространства называют собственными. Приведем примеры собственных линейных подпространств.

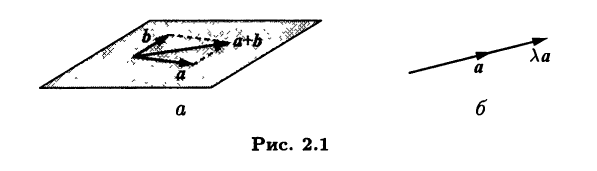
Пример 2.1. В линейном пространстве V₃ свободных векторов трехмерного пространства линейное подпространство образуют: а) все векторы, параллельные данной плоскости; б) все векторы, параллельные данной прямой. Это вытекает из следующих соображений. Из определения суммы свободных векторов [III] следует, что два вектора а, b и их сумма а + b компланарны (рис. 2.1, а). Поэтому, если а и b параллельны данной плоскости, то этой же плоскости будет параллельна и их сумма. Тем самым установлено, что для случая а) выполнено условие 1) определения 2.1. Если вектор умножить на число, получится вектор, коллинеарный исходному (рис. 2.1,6). Это доказывает выполнение условия 2) определения 2.1. Случай б) обосновывается аналогично.

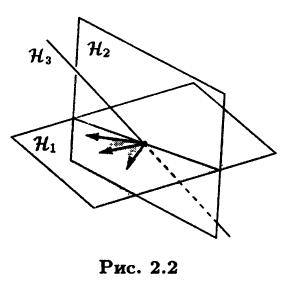
Линейное пространство V₃ дает наглядное представление о том, что такое линейное подпространство. Действительно, фиксируем некоторую точку в пространстве. Тогда различным плоскостям и различным прямым, проходящим через эту точку, будут соответствовать различные линейные подпространства из V₃ (рис. 2.2).

Не столь очевидно, что в V₃ нет других собственных подпространств. Если в линейном подпространстве Н в V₃ нет ненулевых векторов, то H - нулевое линейное подпространство, являющееся несобственным. Если в H есть ненулевой вектор, а любые два вектора из H коллинеарны, то все векторы этого линейного подпространства параллельны некоторой прямой, проходящей через фиксированную точку. Следовательно, H совпадает с одним из линейных подпространств, описанных в случае б). Если в Н есть два неколлинеарных вектора, а любые три вектора компланарны, то все векторы такого линейного подпространства параллельны некоторой плоскости, проходящей через фиксированную точку. Это случай а). Пусть в линейном подпространстве Н существуют три некомпланарных вектора. Тогда они образуют базис в V₃. Любой свободный вектор можно представить в виде линейной комбинации этих векторов. Значит, все свободные векторы попадают в линейное подпространство Н, и поэтому оно совпадает с V₃. В этом случае мы получаем несобственное линейное подпространство.

Итак, в V₃ все собственные подпространства можно пред-ставить в виде плоскостей или прямых, проходящих через фиксированную точку.

Пример 2.2. Любое решение однородной системы линейных алгебраических уравнений (СЛАУ) от n переменных можно рассматривать как вектор в линейном арифметическом пространстве Rⁿ. Множество всех таких векторов является линейным подпространством в Rⁿ. В самом деле, решения однородной СЛАУ можно покомпонентно складывать и умножать на действительные числа, т.е. по правилам сложения векторов из Rⁿ. Результат операции снова будет решением однородной СЛАУ (см. [III]). Значит, оба условия определения линейного подпространства выполнены.

Уравнение х + у - 5z = 0 имеет множество решений, кото-рое является линейным подпространством в R³. Но это же уравнение можно рассматривать как уравнение плоскости в некоторой прямоугольной системе координат Oxyz. Плоскость проходит через начало координат, а радиус-векторы всех точек плоскости образуют двумерное подпространство в линейном пространстве V₃.

Множество решений однородной СЛАУ

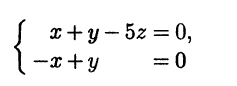
также образует линейное подпространство в R³. В то же время эту систему можно рассматривать как общие уравнения прямой в пространстве, заданные в некоторой прямоугольной системе координат Oxyz. Эта прямая проходит через начало координат, а множество радиус-векторов всех ее точек образует одномерное подпространство в V₃.

Пример 2.3. В линейном пространстве М_n(R) квадратных матриц порядка n линейное подпространство образуют: а) все симметрические матрицы; б) все кососимметрические матрицы; в) все верхние (нижние) треугольные матрицы. При сложении таких матриц или умножении на число мы получаем матрицу того же вида. Напротив, подмножество вырожденных матриц не является линейным подпространством, так как сумма двух вырожденных матриц может быть невырожденной матрицей:

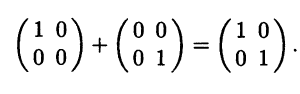
Пример 2.4. В линейном пространстве С[0,1] функций, непрерывных на отрезке [0,1], можно выделить следующие ли-нейные подпространства: а) множество функций, непрерывных на отрезке [0,1] и непрерывно дифференцируемых в интервале (0,1) (в основе этого утверждения лежат свойства дифференцируемых функций: сумма дифференцируемых функций есть дифференцируемая функция, произведение дифференцируемой функции на число есть дифференцируемая функция); б) множество всех многочленов; в) множество К_n[х] всех многочленов степени не выше n. Напротив, множество всех монотонных функций, непрерывных на отрезке [0,1], очевидно, является подмножеством С[0,1], но не является линейным подпространством, так как сумма двух монотонных функций может и не быть монотонной функцией. #

Пусть в линейном пространстве L задана система векторов e₁, е₂, ..., е_k. Рассмотрим множество Н всех векторов в L, которые могут быть представлены линейной комбинацией этих векторов. Это множество является линейным подпространством в L. Действительно, пусть

х = х₁е₁ +... + x_ke_k, у = y_xe₁ + ... + y_ke_k.

Тогда

х + у = (х₁ + y₁)e₁ + ... + (x_k + y_k)e_k ∈ H,

λx = (λx₁)e₁ +... + (λx_k)e_k ∈ Н,

где λ ∈ R. Описанное линейное подпространство называют линейной оболочкой системы векторов e₁, e₂, ..., е_k и обозначают span{e₁,e₂,...,е_k}.

Примечательно то, что любое собственное линейное подпространство можно представить как линейную оболочку некоторой системы его векторов (это будет ясно из дальнейшего изложения). В этом состоит универсальный способ описания линейных подпространств. Отметим, что само линейное пространство является линейной оболочкой любого из своих базисов.

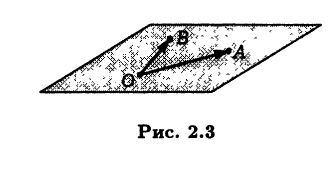
Пример 2.5. Рассмотрим плоскость π, проходящую через три произвольные точки О, А, В, не лежащие на одной прямой. Тогда линейное подпространство векторов, компланарных плоскости π, представляет собой линейную оболочку двух свободных векторов, соответствующих геометрическим векторам OA и OB (рис. 2.3). Действительно, любой вектор,компланарный векторам OA и OB, представляется в виде их линейной комбинации [III].

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ