Размерность линейного пространства

Эта важнейшая характеристика линейного пространства связана со свойствами систем векторов в этом пространстве.

Определение 1.5. Максимальное количество линейно независимых векторов в данном линейном пространстве называют размерностью линейного пространства.

Если размерность линейного пространства L равна n, т.е. существует линейно независимая система из n векторов, а любая система векторов, содержащая n + 1 вектор или более, линейно зависима, то говорят, что это линейное пространство n-мерно. Размерность такого линейного пространства обозначают n = dimL.

Существуют линейные пространства, в которых можно выбрать линейно независимую систему, содержащую сколь угодно большое количество векторов. Такие линейные пространства называют бесконечномерными. В отличие от них,n-мерные линейные пространства называют конечномерными. Эта книга посвящена конечномерным линейным пространствам.

Пример 1.12.. Линейное пространство С[0,1] функций, непрерывных на отрезке [0,1] (см. 1.1), является бесконечно-мерным, так как для любого натурального n система многочленов 1, х, х², ..., хⁿ, являющихся элементами этого линейного пространства, линейно независима. В самом деле, линейная комбинация этих многочленов, отвечающая набору коэффициентов α₀, α₁, ..., α_n, есть многочлен

α₀ + α₁х +... + а_nхⁿ,

который является нулевым (т.е. равен постоянной функции 0) , только если все его коэффициенты (они же коэффициенты линейной комбинации) равны нулю. #

Оказывается, что размерность линейного пространства тесно связана с количеством векторов, которое может иметь базис линейного пространства.

Теорема 1.4. Если линейное пространство L n-мерно, то любая линейно независимая система из n векторов является его базисом.

◄ Пусть система векторов b₁, ..., b_n ∈ L линейно независима. Тогда для любого вектора х ∈ L система векторов х, b₁, ..., b_n линейно зависима, так как она содержит n + 1 вектор, т.е. количество большее, чем размерность линейного пространства. Это значит, что существуют такие коэффициенты α₀, α₁, ..., α_n, одновременно не равные нулю, что

α₀x + α₁b₁ + ... + α_nb_n = 0 (1.6)

Заметим, что α₀ ≠ 0, так как в противном случае равенство (1.6) сводится к равенству

α₁b₁ + ... + α_nb_n = 0,

причем среди коэффициентов α₁, ..., a_n есть хотя бы один ненулевой (так как α₀ = 0). Но это означало бы, что система векторов b₁, ..., b_n линейно зависима.

Учитывая, что α₀ ≠ 0, из (1.6) находим

x = - α₁/α₀ b₁ - ... - α_n/α₀ b_n.

Так как вектор х был выбран произвольно, заключаем, что любой вектор в линейном пространстве L можно представить в виде линейной комбинации системы векторов b₁, ..., b_n. Поэтому эта система векторов, по предположению линейно независимая, является базисом в L. ►

Теорема 1.5. Если в линейном пространстве L существует базис из n векторов, то dimL = n.

◄ Пусть b = (b₁ ... b_n) - базис в линейном пространстве L. Нам достаточно показать, что любая система х₁, ..., x_n+1 из n + 1 вектора из L линейно зависима.

Разложим каждый из этих векторов x_i по базису b:

x₁ = b₁₁b₁ + ... + a_n1b_n,

.........................

x_n+1 = b_1,n+1b₁ + ... + a_n,n+1b_n,

а из столбцов координат векторов x_i составим матрицу

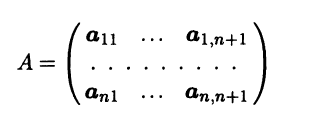
типа n×(n + 1). Согласно следствию 1.1, линейная зависимость системы векторов x, ... ,х _n+1 равносильна линейной зависимости столбцов матрицы А, так как выполнение каких-либо линейных операций над векторами идентично выполнению тех же операций над их столбцами координат. Но в матрице А содержится n строк, поэтому ее ранг не превосходит n. Следовательно, при любом выборе базисного минора хотя бы один из столбцов матрицы не является базисным и по теореме о базисном миноре [III] является линейной комбинацией базисных. Но тогда такое же соотношение справедливо для соответствующих векторов. Следовательно, согласно необходимому и достаточному условию линейной зависимости (см. теорему 1.1), система векторов x₁, ..., x_n+1 линейно зависима, так как один из них равен линейной комбинации остальных. ►

Из теорем 1.4 и 1.5 следует, что в каждом линейном пространстве любые два базиса содержат одно и то же количество векторов, и это количество равно размерности линейного пространства.

Пример 1.13. В линейном арифметическом пространстве Rⁿ стандартный базис (1.5) состоит из n векторов, поэтому dimRⁿ = n, что и отражено в обозначении этого линейного пространства. 

Пример 1.14. Рассмотрим однородную СЛАУ

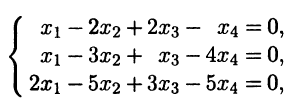
множество решений которой образует линейное пространство. Найдем размерность этого линейного пространства и какой - либо базис в нем.

Следуя [III], решим эту систему, определив ее фундаментальную систему решений. Для этого запишем матрицу системы и при помощи элементарных преобразований строк приведем ее к треугольному виду:

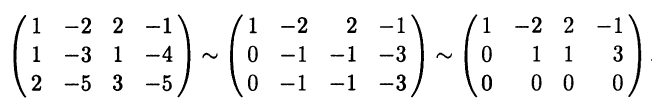
Из полученного вида находим, что ранг матрицы системы равен 2, в качестве свободных неизвестных можно взять х₃ и x₄, а в качестве базисных неизвестных - x₁ и x₂. Преобразованная система имеет вид

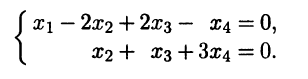
Полагая х₃ = 1, x₄ = 0, находим x₂ = -1, x₁ = -4, а при х₃ = 0, x₄ = 1 имеем x₂ = -3, x₁ = -5. Записав найденные решения в виде столбцов, получим фундаментальную систему решений:

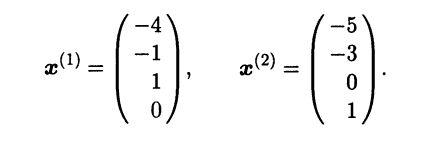
Согласно теории систем линейных алгебраических уравнений [III], эти два решения линейно независимы, а любое другое решение СЛАУ представляется в виде линейной комбинации х⁽¹⁾ и х⁽²⁾. Другими словами, столбцы х⁽¹⁾ и х⁽²⁾ образуют базис в линейном пространстве решений рассматриваемой однородной СЛАУ. Размерность этого линейного пространства равна двум - количеству векторов в базисе.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ