Линейные операции в координатной форме

Фиксация порядка векторов в базисе преследует еще одну цель - ввести матричные способы записи векторных соотношений. Базис b₁, ..., b_n в данном линейном пространстве С удобно записывать как матрицу-строку

b = (b₁ ... b_n),

а координаты вектора х в этом базисе - как матрицу-столбец:

Тогда разложение х = х₁b₁ + ... +х_nb_n вектора х по базису b₁, ..., b_n можно записать как произведение матрицы-строки на матрицу-столбец:

х = bх. (1.4)

Пример 1.9. Векторы ортонормированного базиса в V₃ имеют стандартное обозначение и порядок: i, j, k. В матричной записи это будет выглядеть так: b = (i j к). Вектор, например, с координатами - 1, 2, 2 может быть представлен в виде

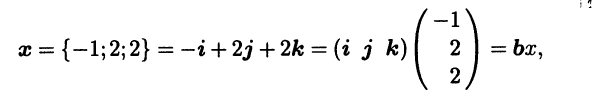
где x = (-1 2 2)^T - столбец координат вектора х. #

Запись линейных операций над свободными векторами в координатной форме [III] обобщается на случай произвольного линейного пространства.

Теорема 1.3. При сложении любых двух векторов в линейном пространстве их координаты в одном и том же базисе складываются, а при умножении вектора на число его координаты умножаются на это число.

◄ Рассмотрим в линейном пространстве L базис b = (b₁ ... b_n). Пусть даны разложения векторов х и у в этом базисе:

x = x₁b₁ +...+ х_nb_n, у = у₁b₁ +... + у_nb_n.

В силу аксиом линейного пространства

х + у = (x₁b₁ +... + x_nb_n) + (у₁b₁ +... + у_nb_n) = (x₁ + y₁)b₁ + ... + (x_n + у_n)b_n.

Таким образом, при сложении двух векторов их координаты, отвечающие одному базисному вектору, складываются. В матричной записи координат этому соответствует матричная сумма столбцов координат.

Аналогично для произвольного действительного числа λ

λх = λ(x₁b₁ + ... + х_nb_n) = (λ₁)b₁ +... + (λх_n)b_n,

т.е. при умножении вектора на число каждая из его координат умножается на это число. ►

Запись координат векторов в матричной форме снимает вопрос о том, что понимать, например, под сложением координат: координаты складываются как матрицы-столбцы. Аналогично столбец координат умножается на число по правилам умножения матрицы на число. Запись^утверждения теоремы 1.3 в матричной форме

bx + by = b(х + у), λbх = b(λх)

соответствует свойствам матричных операций: дистрибутивности сложения относительно умножения и ассоциативности умножения.

Следствие 1.1. Линейная независимость (зависимость) векторов линейного пространства эквивалентна линейной независимости (зависимости) их столбцов координат в одном и том же базисе этого линейного пространства.

◄ Если вектор а равен линейной комбинации векторов a₁, ..., а_k, т.е.

а = α₁a₁ + ... + α_ka_k,

то его столбец координат а в заданном базисе b равен такой же линейной комбинации столбцов координат a₁, ..., а_k векторов a₁, ..., а_k в этом же базисе:

а = α₁a₁ + ... + α_ka_k.

Это следует из равенств:

bа = а = α₁а₁ +... + α_ka_k = а₁(bа₁) + ... + а_k(bа_k) = b(α₁а₁ +... + α_kа_k). ►

Пример 1.10. В линейном арифметическом пространстве Rⁿ векторы

e₁ = (l, 0, .... 0),

e₂ = (0, 1, ..., 0),       (1.5)

.........................

е_n = (0, 0, ... , 1)

образуют базис e = (e₁ ... e_n), так как они линейно независимы (см. пример 1.5) и любой вектор х = (x₁, ..., х_n) ∈ Rⁿ представим в виде х = х₁е₁ +... + х_nе_n. #

Базис (1.5) в пространстве Rⁿ называют стандартным.

Замечание 1.4. В линейном арифметическом пространстве Шп для произвольного вектора х = (х₁, ..., х_n) его столбец координат х в стандартном базисе совпадает с x^T. Как и в аналитической геометрии [III], удобно при фиксированном базисе отождествлять вектор с его координатами. Для стандартного базиса это равносильно записи вектора не как матрицы-строки, а как матрицы-столбца. Отметим, что запись элементов арифметического пространства в виде столбца не противоречит определению арифметического пространства, понимаемого как множество упорядоченных совокупностей чисел. Порядок же элементов можно указывать как при помощи записи в строку, так и при помощи записи в столбец.

Пример 1.11. Покажем, что в R³ система векторов

a₁ = (1, -1, 2), a₂ = (2, 1,0), a₃ = (4, -1,1)

образует базис и найдем в этом базисе координаты вектора с = (2, 1, 3).

Для того чтобы доказать, что система векторов a₁, a₂, а₃ образует базис, надо убедиться в линейной независимости этих векторов и в том, что любой вектор b = (b₁, b₂, b₃) ∈ R³ является их линейной комбинацией.

В стандартном базисе е в R³ векторы a₁, a₂, а₃, b, с имеют следующие столбцы координат:

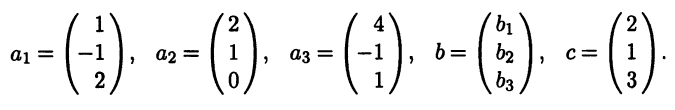
Из столбцов координат векторов a₁, а₂, a₃ составим матрицу

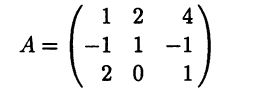
и рассмотрим квадратную систему линейных алгебраических уравнений (СЛАУ) Ах = b, х = ( х₁ x₂ х₃) . Так как detА = -9, то матрица А невырожденная, ее ранг равен 3 и все ее столбцы являются базисными. Поэтому, во-первых, согласно теореме о базисном миноре [III], эти столбцы линейно независимы, что, согласно следствию 1.1, означает линейную независимость векторов a₁, a₂, а₃, а во-вторых, СЛАУ Ах = b при любом столбце b правых частей имеет решение х = (х'₁ х'₂ х'₃) , что после записи этой СЛАУ в векторной форме [III]

a₁x₁ + a₂x₂ + a₃x₃ = b.

позволяет сделать вывод о выполнении равенства

x'₁a₁ + x'₂a₂ + x'₃a₃ = b.

В частности, решив СЛАУ Ах = с, которая в координатной форме имеет вид

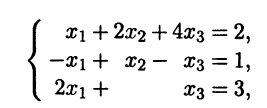
находим координаты вектора с в базисе (a₁ a₂ а₃): х₁ = 2, x₂ = 2, x₃ = -1.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ