Свойства систем векторов

Непосредственно из аксиом линейного пространства можно получить ряд простейших свойств систем векторов произвольного линейного пространства L.

1°. Если среди векторов x₁, x₂,..., x_k ∈ L есть нулевой вектор, то эта система векторов линейно зависима.

◄ Пусть, например, x₁ = 0. Тогда линейная комбинация 1 • x₁ + 0 • x₂ + ... + 0 • x_k является нетривиальной, так как первый ее коэффициент равен единице. В то же время указанная линейная комбинация равна 0, потому что все ее слагаемые равны нулевому вектору. ►

2°. Если система векторов содержит линейно зависимую подсистему, то она линейно зависима.

◄ Подсистема состоит из части векторов исходной системы. Пусть, например, в системе векторов х₁, ..., х_k подсистема x₁, ... , х_m, m < n, линейно зависима. Это значит, что можно указать коэффициенты α₁, ..., α_m, одновременно не равные нулю, для которых

α₁x₁ + ... + α_mx_m = 0

Введя дополнительные коэффициенты α_m+1 = ... = α_k = 0, получим линейную комбинацию системы векторов х₁, ..., x_m, x_m+1, ... , х_k. С одной стороны, она не является тривиальной, так как среди первых ее m коэффициентов есть ненулевые, а с другой стороны,

α₁x₁ + ... + α_mx_m + α_m+1x_m+1 ... + α_kx_k = 0 + 0 • x_m+1 + ... + 0 • x_k = 0,

так как все коэффициенты начиная с (m + 1)-го равны нулю. Следовательно, исходная система векторов линейно зависима. ►

3°. Если система векторов линейно независима, то и любая ее подсистема тоже линейно независима.

◄ Это свойство является переформулировкой предыдущего. В самом деле, по свойству 2° система, имеющая линейно зависимую подсистему, не может быть сама линейно независимой. Поэтому у линейно независимой системы вообще не может быть линейно зависимых подсистем. ►

4°. Если векторы e₁, ..., е_m линейного пространства L линейно независимы и вектор у ∈ L не является их линейной комбинацией, то расширенная система векторов e₁, ..., e_m, у является линейно независимой.

◄ Действительно, пусть

α₁e₁ + ... + α_me_m + βy = 0

Тогда коэффициент β должен быть нулевым, так как в противном случае мы можем выразить вектор у через остальные. Но слагаемое βу в равенстве слева можно при β = 0 опустить, и мы получаем линейную комбинацию векторов e₁, ..., е_k, равную нулевому вектору. В силу линейной независимости этих векторов все коэффициенты линейной комбинации равны нулю. Значит, исходная линейная комбинация является тривиальной и поэтому система векторов е_m, ..., е_m, у линейно независима. ►

Пример 1.5. В линейном арифметическом пространстве Rⁿ рассмотрим n векторов

e₁ = (l, 0,...,0, 0),

е₂ = (0, 1,...,0, 0),

...........................

е_n = (0, 0,...,0, 1).

Докажем, что система из этих векторов линейно независима. Так как для любых коэффициентов α₁ , .... ,α_n

α₁e₁ + α₂e₂ + ... + α_ne_n = (α₁, α₂, ... , α_n)

то ясно, что эта линейная комбинация векторов e₁,..., е_n может быть равна нулевому вектору 0 = (0, 0, ..., 0) только лишь при условии, что α₁ = α₂ = ... = α_n = 0. Это и означает, что эта система векторов линейно независима.

Отметим, что если из векторов е₁, ..., е_n, рассматривая их как строки одинаковой длины, составить матрицу

то ее ранг будет максимальным (RgЕ = n), так как Е является невырожденной матрицей. По теореме о базисном миноре [III] строки этой матрицы линейно независимы. Таким образом, понятие линейной независимости векторов e₁, ..., е_n линейного арифметического пространства в данном случае согласуется с понятием линейной независимости строк единичной матрицы Е.

Пример 1.6.. Любые два коллинеарных вектора на плоскости (в V₂) и любые три компланарных вектора в пространстве (в V₃) линейно зависимы. И в том, и в другом случае один из векторов можно представить в виде линейной комбинации другого (других) [III]. По этой же причине в пространстве линейно зависима любая система из четырех векторов.

Пример 1.7. Пусть в произвольном линейном пространстве L даны два вектора d₁ и d₂ и пусть а = 3d₁ - 2d₂, b = 2d₁ + 3d₃, с = d₁ + 5d₂. Тогда система векторов а, b, с линейно зависима.

В самом деле, составим линейную комбинацию системы векторов а,b, с с произвольными коэффициентами х, у, z и приравняем ее нулевому вектору: ха + yb + zc = 0. В этой линейной комбинации заменим векторы их представлениями через d₁ и d₂:

xa + yb + zc = x(3d₁ - 2d₂) + y(2d₁ + 3d₂) + z(d₁ + 5d₂) = (3x + 2y + z)d₁ + (-2x + 3y + 5z)d₂.

Теперь достаточно приравнять нулю коэффициенты при d₁ и d₂, чтобы получить нулевую линейную комбинацию. Значит, если коэффициенты х, у, z удовлетворяют системе линейных алгебраических уравнений

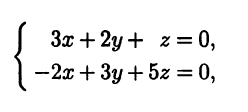
то линейная комбинация векторов a, b, с с коэффициентами х, у, z равна нулевому вектору. Как следует из теории систем линейных алгебраических уравнений [III], указанная система всегда имеет ненулевое решение, поскольку ранг ее матрицы равен двум и меньше трех - количества неизвестных. Например, ненулевым решением является х = 7, у = -17, z = 13. Значит, существуют такие х, у, z, одновременно не равные нулю, что линейная комбинация векторов а, b, с с этими коэффициентами равна нулевому вектору, т.е. система векторов а, b, с линейно зависима.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ