Свойства линейного пространства
Теория- Автор
- Издательство
Непосредственно из аксиом линейного пространства можно получить ряд простейших свойств.
Свойство 1.1.. Любое линейное пространство имеет только один нулевой вектор.
◄ В аксиоме в) линейного пространства не утверждается, что нулевой вектор должен быть единственным. Но из аксиом а) и в) в совокупности это вытекает. Пусть существуют два нулевых вектора 0 и 0'. Тогда

Здесь в роли нулевого элемента сначала выступает вектор 0', а затем 0. Видим, что векторы 0 и 0' совпадают. ►
Свойство 1.2. Каждый вектор линейного пространства имеет только один противоположный вектор.
порядка выполнения двух операций сложения. Меняя порядок сложения, получаем:
Пусть для вектора x существуют два противоположных вектора (-х) и (-x)'. Согласно аксиоме г) линейного пространства это означает, что х + (-x) = 0 и x + (-x)' = 0. Рассмотрим двойную сумму (-x) + x + (-x)' элементов линейного пространства. Согласно аксиоме б) эта сумма не зависит от порядка выполнения двух операций сложения. Меняя порядок сложения, получаем:

Свойство 1.3. Если вектор (-x) противоположен вектору х, то вектор х противоположен вектору (-x).
◄ Утверждение опирается на коммутативность сложения. Действительно,
"(-x) противоположен x" + ⇔ x + (-x) = 0,
"x противоположен (-x)" ⇔ (-x) + x = 0.
Справа стоят эквивалентные равенства (в силу аксиомы а)). Значит, и утверждения слева равносильны. ►
Свойство 1.4. Для любых двух векторов a и b уравнение a + х = b относительно х имеет решение, и притом единственное.
◄ Существование. Решением уравнения a + x = b является вектор (-а) + b, так как
а + ((-а) + b) = (а + (-а)) + b = 0 + b = b.
Единственность. Пусть х - какое-либо решение указанного уравнения, т.е. выполнено равенство a + х = b. Прибавив к обеим частям этого равенства вектор (-a), получим (-a) + а + х = (-a) + b, откуда x = (-a) + b. Видим, что вектор х совпал с указанным выше решением (-а) + b. Значит, других решений нет. ►
Последнее свойство позволяет ввести еще одну операцию в линейном пространстве, которая является противоположной сложению. Разностью двух векторов b - a называют вектор x, являющийся решением уравнения а + х = b (вспомним, что разностью двух чисел b - а называют такое число, которое в сумме с вычитаемым а дает уменьшаемое Ь). Из доказательства свойства 1.4 вытекает, что
b - а = b + (-a) = (-a) + b.
Свойство 1.5. Произведение произвольного элемента линейного пространства на число 0 равно нулевому вектору: 0 • х = 0.
◄ Отметим, что решением уравнения х + у = х относительно неизвестного у является нулевой вектор (аксиома в)). Покажем, что в качестве решения этого уравнения можно взять и вектор 0 • x, который тогда, в силу единственности решения, будет совпадать с 0. Итак, проверяем:
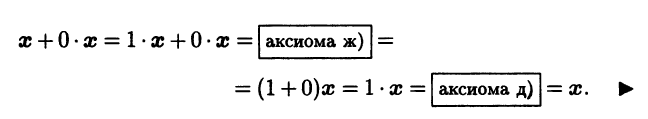
Свойство 1.6. Вектор, противоположный данному вектору x, равен произведению x на число -1: (-x) = (-1)x.
◄ Благодаря единственности противоположного вектора (свойство 1.2) достаточно доказать, что вектор (-1)x удовлетворяет аксиоме г) линейного пространства. Для этого используем аксиому дистрибутивности ж) и только что доказанное свойство 1.5:
x + (-1)x = 1 • x + (-1)x = (1 + (-1))x = 0 • x = 0. ►
Замечание 1.2. Эквивалентность равенств а + x = b и x = b - а можно трактовать как правило, согласно которому слагаемое, которое переносят в другую часть равенства, меняет свой знак. Ясно также, что для α ∈ R из равенства a = b следует равенство αa = αb и наоборот (при α ≠ 0), так как
1/α(αа) = (1/α α) а = 1 • a = a /
и аналогично
1/α(αb) = b.
Свойство 1.7. Произведение нулевого вектора на любое число есть нулевой вектор: λ0 = 0.
◄ Мы теперь знаем, что нулевой вектор можно представить как произведение произвольного вектора (того же 0) на число 0 (свойство 1.5). Используя это, получаем:
λ0 = λ(0•0) = (λ • 0)0 = 0 • 0 = 0. ►
Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ