Определение линейного пространства

Центральное место в линейной алгебре занимает следующее понятие.

Определение 1.1. Множество L элементов х, у, z, ... любой природы называют линейным пространством, если выполнены три условия:

1) задано сложение элементов L, т.е. закон, по которому любым элементам х,у ∈ L ставится в соответствие элемент x ∈ L, называемый суммой элементов х и у и обозначаемый z = x + y,

2) задано умножение элемента на число, т.е. закон, по которому любому элементу х ∈ L и любому числу λ ∈ R ставится в соответствие элемент z ∈ L, называемый произведением элемента х на (действительное) число и обозначаемый z = λх;

3) указанные законы (линейные операции) подчиняются следующим аксиомам линейного пространства:

а) сложение коммутативно: х + у = у + х;

б) сложение ассоциативно: (x + y) + z = x + (y + z);

в) существует такой элемент 0 ∈ L, что х + 0 = х для любого х ∈ L;

г) для каждого элемента х множества L существует такой элемент (-х) ∈ L, что х + (-х) = 0;

д) произведение любого элемента х из L на единицу равно этому элементу: 1 х = х;

е) умножение на число ассоциативно: λ(μх) = (λμ)х;

ж) умножение на число и сложение связаны законом дистрибутивности по числам: (λ + μ)х = λх + μх;

з) умножение на число и сложение связаны законом дистрибутивности по элементам: λ(х + у) = λх + λу.

Элементы линейного пространства принято называть векторами. Элемент 0, существование которого постулируется аксиомой в), называют нулевым вектором, а элемент (-x) - вектором, противоположным к вектору х.

В понятии "линейное пространство" важно не только рассматриваемое множество L, но и заданные операции сложения элементов и умножения на число. Одно и то же множество L при одних операциях может быть линейным пространством, а при других - нет. Фактически линейным пространством является совокупность (L,+,•) из множества элементов и двух операций, которая удовлетворяет условиям определения 1.1. В этой тройке объектов базовым все-таки является множество L, так как операции вводятся именно на этом множестве. Поэтому понятие линейного пространства обычно ассоциируют с множеством элементов L и говорят, что L - линейное пространство. При этом, как правило, очевидно, что понимается под операциями линейного пространства. Если же требуется явно указать используемые операции, то говорят: множество L - линейное пространство относительно таких-то операций.

Согласно определению 1.1 линейного пространства L сумма определена для любых элементов из L и всегда является элементом множества L. Подчеркивая последнее, говорят, что множество L замкнуто относительно операции сложения. Аналогично, согласно тому же определению, множество L замкнуто относительно операции умножения его элементов на действительные числа.

Пример 1.1. Приведем примеры линейных пространств:

- множество V₃ (V₂) всех свободных векторов в пространстве (на плоскости) с линейными операциями над векторами - линейное пространство, так как верны все аксиомы линейного пространства [III];

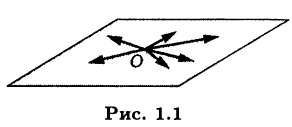
- множество всех геометрических векторов в пространстве с началом в данной точке и параллельных данной плоскости (рис. 1.1) с линейными операциями над векторами является линейным пространством [III];

5. 1) -2; 2) 5; 3) 1; 4) -8; 5) -2 и 2; 6) -1 и 5; 7) -6 и 4; 8) -7 и -3.

- множество М_mn(R) матриц типа m × n, элементами которых являются действительные числа, с линейными операциями над матрицами также удовлетворяет всем аксиомам линейного пространства;

- множество матриц-строк (матриц-столбцов) длины n является линейным пространством относительно матричных операций сложения и умножения на число (это частный случай предыдущего примера);

- множество К_n[х] многочленов переменного х степени, не превышающей n, которые как функции можно складывать и умножать на действительные числа;

- множество всех решений данной однородной системы линейных алгебраических уравнений (СЛАУ). Решения можно рассматривать как матрицы-столбцы, складывать и умножать на числа по законам матричных операций [III]. Столбец, получаемый в результате сложения решений или умножения решения на число, снова будет решением системы. Поэтому определены операции, о которых говорится в определении 1.1, подчиняющиеся аксиомам линейного пространства;

- множество функций, непрерывных на отрезке, с обычными операциями сложения функций и умножения функции на число. При сложении непрерывных функций получаем непрерывную функцию, при умножении непрерывной функции на число также получаем непрерывную функцию. Поэтому сложение функций и умножение функции на число, не выводящие за пределы множества непрерывных на отрезке функций, можно рассматривать как операции линейного пространства. Легко убедиться, что для этих операций верны все аксиомы линейного пространства.

Пример 1.2. Рассмотрим множество R₊ всех действительных положительных чисел. Если суммой элементов ж, у ∈ R₊ -считать обычную сумму действительных чисел x + у, а проиведением действительного числа λ на элемент х ∈ R₊ - обычную операцию произведения действительных чисел Аж, то мы не получим линейного пространства, так как при λ = 0 обычная операция умножения действительных чисел дает λ • x = 0, т.е. умножение на нуль дает число, не принадлежащее множеству R₊, а значит, множество R₊ не замкнуто относительно этой операции умножения на действительные числа, т.е. нарушается условие 2) определения 1.1.

Введем операции на множестве R₊ по-другому. " Суммой " x ⊕ у элементов x и у назовем произведение этих элементов как действительных чисел: x ⊕ у = xу. " Произведением" λ 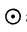x элемента x ∈ R₊ на число λ ∈ R назовем возведение x как числа в действительную степень λ: λ 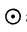x = x^λ. Видоизмененное обозначение введенных операций ⊕ и 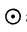подчеркивает их необычную трактовку.

"Сумма" x ⊕ у и ппроизведение" λ 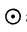x, как нетрудно увидеть, определены для любых пар x,у ∈ R₊ и λ ∈ R, x ∈ R₊ соответственно. Кроме того, множество R₊ замкнуто отнсительно этих операций. Убедимся, что для этих операций верны аксиомы линейного пространства. Для любых элементов ж,y,z ∈ R₊ и любых действительных чисел λ, μ, учитывая свойства умножения и возведения в степень действительных чисел, получаем:

а) x ⊕ у = xу = уx = у ⊕ ж;

б) (x ⊕ у) ⊕ z = (xy)z = x(yz) = х ⊕ (у ⊕ z);

в) в качестве нулевого элемента 0 следует взять число 1, так как x ⊕ 0 = x • 1 = x для любого элемента x;

г) противоположным произвольному элементу x ∈ R₊ будет элемент (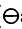x) - 1/x, так как x ⊕ (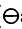x) = x(1/x) = 1 = 0;

д) " умножение " элемента на число 1 его не меняет: 1 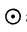x = = x¹ = x;

е) λ 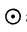(μ 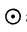x) = (x^μ)^λ = x^μλ = x^λμ = (λμ) 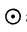х;

ж) (λ + μ) 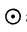x = x^{λ + μ} = х^λх^μ = (λ 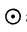х) ⊕ (μ 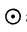x);

з) λ 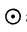(х ⊕ у) = (xу)^λ = x^λу^λ = (λ 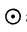х) ⊕ (λ 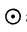у).

Итак, заключаем, что все восемь аксиом линейного пространства выполнены. Значит, множество R₊ с введенными операциями ⊕ и 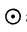является линейным пространством.

Пример 1.3. На множестве Rⁿ = {х: х = (x₁, ..., x_n)}, элементами которого являются упорядоченные совокупности п произвольных действительных чисел, введем операции

х + у = (x₁ + y₁, ..., x_n + y_n), λх = (λx₁, ..., λх_n), λ ∈ R.

Тогда получим линейное пространство, так как все аксиомы линейного пространства для данных операций выполняются. Это линейное пространство, по сути, есть линейное простран-ство матриц-строк. Отличие лишь формальное, так как первое определено как множество упорядоченных наборов чисел, а второе как множество матриц. Но элементы матрицы всегда записывают в определенном порядке. Линейное пространство Rⁿ называют линейным арифметическим пространством.

Замечание 1.1. Операция умножения вектора на число в определении 1.1 задана только для действительных чисел. Но точно так же можно ввести линейное пространство с умножением элементов множества L на произвольные комплексные числа. Два способа определения линейного пространства различают, используя термины "линейное пространство над полем действительных чисел " (более коротко: действительное линейное пространство) и "линейное пространство над полем комплексных чисел" (комплексное линейное пространство). Теории в этих двух случаях очень близки, но различия все-таки есть. Важный пример комплексного линейного пространства - комплексное арифметическое пространство

Cⁿ = {z:z = (z₁, ..., z_n)},

элементами которого являются упорядоченные наборы из п комплексных чисел. Операции в этом пространстве задаются по тем же правилам, что и в случае действительного арифметического пространства.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ