Умножение матриц
ТеорияОпределение 10.6. Пусть даны матрица А = (аij) типа m×n и матрица B = (bij) типа n×p. Произведением матриц А и В называют матрицу C = (сij) типа m×p с элементами
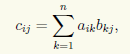
которую обозначают C = AB.
Произведение определено лишь в том случае, когда количество столбцов первого сомножителя равно количеству строк второго. В формировании элемента сij произведения AB участвуют элементы i-й строки матрицы A и j-го столбца матрицы B. Поэтому правило умножения матриц называют также правилом умножения "строка на столбец":
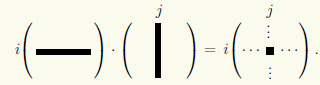
Пример 10.4. Найдем произведение двух матриц
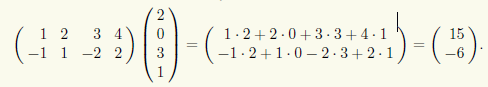
Пример 10.5. Произведением прямоугольной матрицы и матрицы-столбца является матрица-столбец:
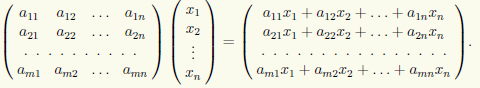
Пример 10.6. Найдем произведение трех квадратных матриц второго порядка, перемножив сначала первые две матрицы, а затем результат их произведения и третью матрицу:
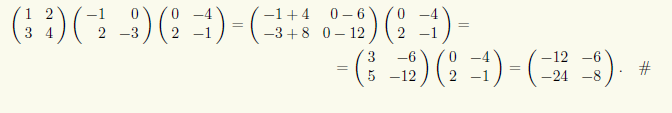
Умножение матрицы-строки X типа 1×n на матрицу-столбец Y типа n×1 дает матрицу типа 1×1, которую отождествляют с числом:
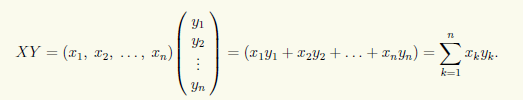
Таким образом, произведение любой матрицы-строки и любой матрицы-столбца, имеющих одинаковое количество элементов, есть число, равное сумме произведений их элементов с одинако-выми индексами. Если матрица-строка и матрица-столбец имеют разное количество элементов, то их перемножить нельзя.
Замечание 10.3. Для числовых матриц типа 1×1 матричные операции суммы, разности, умножения и умножения матриц на действительные числа совпадают с соответствующими арифметическими операциями суммы, разности и умножения, выполняемыми с действительными числами. Вот почему матрицы типа 1×1 отождествляют с числами.
Существование произведения AB двух матриц не означает существования их произведения BA. Например, матрицы из примера 10.4 нельзя умножить в другом порядке.
Чтобы матрицу A типа m×n можно было умножить на матрицу B и слева, и справа (т.е. чтобы были определены оба произведения BA и AB), матрица B должна иметь тип n×m. Квадратные матрицы A и B можно перемножить, если они имеют одинаковый порядок, причем в этом случае определены оба произведения (AB и BA), хотя равенство AB = BA обычно нарушается.
Пример 10.7. Найдем произведения двух пар матриц A, B и C, D в одном и другом порядке:
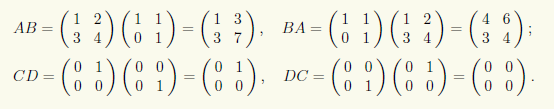
Обратим внимание, что CD = C, DC = Θ, хотя ни одна из этих двух матриц не является нулевой. #
Если определены оба произведения AB и BA и выполнено равенство AB = BA, то матрицы A и B называют коммутирующими или перестановочными. Коммутирующие матрицы всегда квадратные и одного порядка.
Пример 10.8. Произведение диагональных матриц одного порядка есть диагональная матрица, элементами которой являются произведения соответствующих элементов перемножаемых матриц. Диагональные матрицы одного порядка являются перестановочными. Действительно,
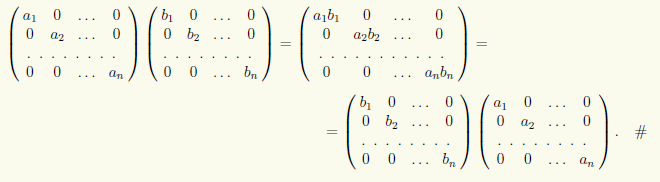
Операция умножения матриц имеет следующие свойства.
1°. Умножение матриц ассоциативно, т.е. (AB)C = A(BC).
◄ Если матрицы А, В, С имеют типы m×n, n×k, k×l соответственно, то
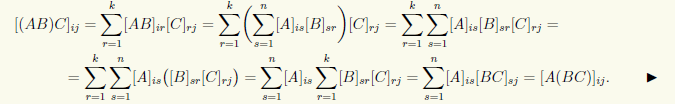
2°. Умножение матриц дистрибутивно относительно сложения матриц, т.е. (A + В)C = AC + BC.
◄ Если матрицы A, В имеют тип mxn, а матрица С — тип n×k, то
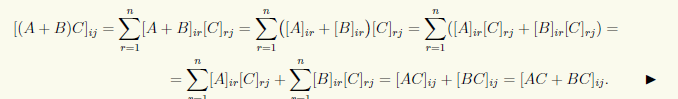
3°. Существует такая матрица E ∈ Mn(R), что для любой матрицы A ∈ Mn(R) выполнены равенства AE = EA = A.
◄ В качестве матрицы E можно взять единичную порядка n. ►
4°. Для любой матрицы A ∈ Mn(R) и нулевой матрицы Θ ∈ Mn(R) выполнено равенство AΘ = Θ.
Вычислим элементы произведения AΘ: [AΘ]ij Σnr=1 [A]ir[Θ]rj = Σnr=1 [A]ir0 = 0. Видим, что все элементы матрицы AΘ равны нулю. ►
5°. Для любых матриц A и B типов m×n и n×k выполнено равенство (AB)T = BTAT, т.е. транспонированное произведение двух матриц равно произведению в обратном порядке транспонированных матриц.
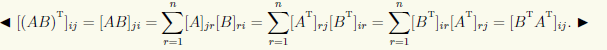
Операция умножения матриц позволяет ввести операцию возведения квадратной матрицы в натуральную степень. Положим A1 = A, An+1 = AAn, n = 1, 2,... Отметим, что две степени An и Am одной и той же матрицы являются матрицами одного порядка и перестановочны: AnAm = AmAn = An+m. Введем также нулевую степень квадратной матрицы, полагая A0 = E, где E — единичная матрица того же порядка.
Введенная степень матрицы позволяет для квадратной матрицы вычислять выражения вида
anAn+ an-1An-1 + ... + a0A0 , ai ∈ R, i = 0,n,
т.е. многочлены от одного матричного аргумента.
Пример 10.9. Вычислим значение квадратного трехчлена p(x) = 3x2 — 4x + 5 для ква-
дратной матрицы 
Поскольку p(x) = 3x2 — 4x + 5x0, то p(A) = 3A2 — 4A + 5A2, где A0 = E — единичная матрица второго порядка. Вычислив  , находим
, находим 