Цилиндрические поверхности
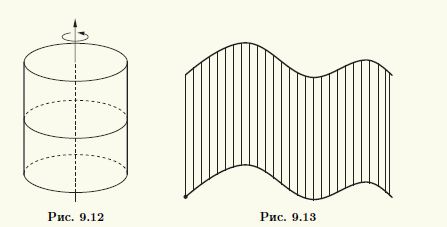
ТеорияПри вращении прямой вокруг некоторой оси, параллельной этой прямой, образуется по-верхность, которую называют круговым цилиндром (рис. 9.12). Эта поверхность является частным случаем цилиндрической поверхности, получающейся при движении прямой в пространстве, которая остается параллельной своему исходному положению (рис. 9.13). Если на движущейся прямой фиксировать точку, то она опишет кривую, которую называют направляющей цилиндрической поверхности (см. рис. 9.13). Можно также сказать, что цилиндрическая поверхность представляет собой множество точек прямых, параллельных фиксированной прямой. Эти параллельные прямые называют образующими цилиндрической поверхности.
В качестве направляющей цилиндра можно взять любую кривую, образованную пересечением цилиндрической поверхности с плоскостью, не параллельной образующим. Выберем прямоугольную систему координат так, чтобы образующие цилиндрической поверхности были параллельны оси Oz. В качестве направляющей выберем кривую, являющуюся пересечением цилиндрической поверхности с координатной плоскостью xOy (рис. 9.14).
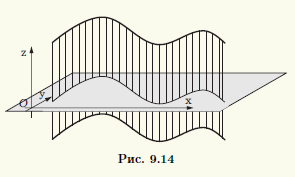
Направляющая в плоскости xOy описывается некоторым уравнением φ(x,y) = 0 двух переменных. Точка M(x; y; z) лежит на цилиндрической поверхности тогда и только тогда, когда ее абсцисса и ордината (фактически координаты точки N(x; у; 0) на плоскости xOy) подчиняются уравнению направляющей. Поэтому в выбранной системе координат цилиндрическая поверхность описывается уравнением φ(x,y) = 0 — уравнением своей направляющей, которое трактуется как уравнение трех переменных x, у и z. Верно и обратное утверждение: если в некоторой прямоугольной системе координат в пространстве поверхность описывается уравнением, не содержащим одного из переменных, то эта поверхность является цилиндрической. Итак, критерием для цилиндрической поверхности является отсутствие в ее уравнении в подходящей системе координат одного из переменных.
Цилиндр второго порядка — это цилиндрическая поверхность, направляющая которой в плоскости, перпендикулярной образующим, представляет собой кривую второго порядка. В выбранной выше прямоугольной системе координат цилиндр второго порядка описывается уравнением второй степени Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0, где A2 + B2 + C2 ≠ 0.
Это уравнение можно упростить подходящим выбором системы координат. Фактически речь идет о приведении к каноническому виду уравнений второго порядка от двух переменных (см. 8.3). Канонические уравнения кривых второго порядка приводят к трем видам цилиндров второго порядка:
- эллиптическому (рис. 9.15, а) с каноническим уравнением x2/a2 + y2/b2 = 1;
- гиперболическому (рис. 9.15, б) с каноническим уравнением x2/a2 + y2/b2 = 1;
- параболическому с каноническим уравнением y2 = 2px (рис. 9.15, в).
Отметим, что если направляющей является пара пересекающихся (параллельных, совпадающих) прямых, то соответствующая им цилиндрическая поверхность представляют собой пару пересекающихся (параллельных, совпадающих) плоскостей.
