Сходимость итерационных методов

Итерационные методы решения систем линейных алгебра-ических уравнений (СЛАУ) наиболее детально разработаны в случае, когда матрица системы симметрическая положитель-но определенная. Это объясняется тем, что такие системы часто встречаются в приложениях, причем они имеют значи-тельные размеры, и прямые методы для таких систем теряют эффективность.

Отметим, что квадратную СЛАУ с невырожденной матрицей А легко преобразовать в эквивалентную систему с симметрической положительно определенной матрицей. Для этого достаточно умножить систему Ах = b слева на матрицу А^T. Поскольку detА^T = det А ≠ 0, то получающаяся при этом СЛАУ А^TАх = А^Tb эквивалентна исходной СЛАУ, так как можно про-вести обратное преобразование, умножив полученную систему слева на матрицу (А^T)^-1. Матрица А^TА является симметрической:

(А^TА)^T = А^T(А^T)^T = А^TА.

Покажем, что она является и положительно определенной. Для этого рассмотрим квадратичную форму х^TА^TАх. В силу свойств умножения матриц имеем

х^TА^TАх = (Ах)^T(Ах) = ||Аx||² ≥ О,

где ||·|| — евклидова норма в линейном арифметическом пространстве Rⁿ со стандартным скалярным умножением. Последнее нестрогое неравенство превращается в равенство, если только столбец Ах является нулевым. Так как матрица А не-вырождена, существует обратная матрица А^-1. Поэтому при Ах = 0 имеем х = Ех = (А^-1А)х = А^-1(Ах) = А^-10 = 0.

Переход от данной СЛАУ к эквивалентной ей системе с симметрической положительно определенной матрицей не все-гда целесообразен. При таком переходе могут утрачиваться свойства, которые были бы полезны при решении системы и которые не компенсируются приобретенными свойствами (симметричностью и положительной определенностью). Например, это наблюдается для разреженных матриц, отличительной особенностью которых является большое количество нулевых элементов. К недостаткам указанного перехода следует отнести и то, что он, как правило, приводит к увеличению числа обусловленности матрицы системы.

Основой любого итерационного метода является сходимость итерационной последовательности по той или иной норме, заданной в линейном пространстве. Мы рассмотрим линейное арифметическое пространство Rn, норма в котором порождается стандартным скалярным умножением. Элементы линейного арифметического пространства будем записывать в виде столбцов.

Если матрица А симметрическая, то запись А > 0 означает, что эта матрица положительно определена. Другими словами, положительно определенной является квадратичная форма х^TАх, матрицей которой является А. Для произвольной матрицы В мы также можем рассмотреть квадратичную форму х^TВх. Матрицей этой квадратичной формы является B^s = (В + В^T)/2. Если указанная квадратичная форма положительно определена, то мы будем говорить, что и матрица В (вообще говоря, несимметрическая) положительно определена и обозначать это так: В > 0.

Рассмотрим одношаговый итерационный метод в канонической форме (11.5). Если метод стационарный, то он определяется частным случаем канонической формы

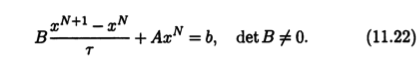
Для такого метода верна следующая теорема о сходимости.

Теорема 11.3 (теорема А.А. Самарского). Если А — симметрическая положительно определенная матрица, r > 0 и матрица В удовлетворяет условию В — 0,5rА > 0, то итерационная последовательность для итерационного метода (11.22) сходится. #

Сформулированная теорема 11.3 позволяет получить легко проверяемые условия сходимости для конкретных итерационных методов.

Следствие 11.1. Пусть А — симметрическая положительно определенная матрица порядка n с диагональным преобладанием, т.е. для ее элементов выполняются неравенства

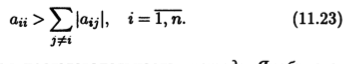
Тогда итерационная последовательность метода Якоби сходится.

Метод Якоби является частным случаем канонической формы (11.22) стационарного итерационного метода при r = 1, В = D. Поэтому условие теоремы 11.3 для этого метода имеет вид 2D — А > 0. Покажем, что это условие выполняется, если матрица А имеет диагональное преобладание.

Оценим квадратичную форму х^TАх, учитывая, что a_ji = a_ijдля симметрической матрицы А:

Из (11.23) немедленно следует, что у матрицы А с диаго-нальным преобладанием диагональные элементы ац положи-тельны. Поэтому при х ≠ 0

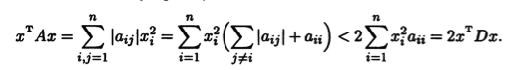
Следовательно, х^T(2D — А)х > 0 при х ≠ 0 и условия теоремы А.А. Самарского выполнены.

Следствие 11.2. Если А — симметрическая положительно определенная матрица, то итерационная последовательность метода верхней релаксации сходится при 0 < ω < 2.

Метод верхней релаксации получается из канонической формы (11.22) стационарного метода при В = D + ωА_, r = ω. Для симметрической матрицы А имеем А^T_ = А₊. Значит, квадратичные формы х^TА_х и х^TА₊х совпадают, так как у них одна и та же матрица 0,5(А_ + A₊). Учитывая это, преобразуем условие теоремы 11.3:

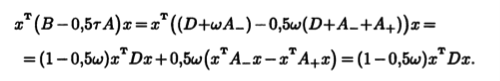
У симметрической положительно определенной матрицы все диагональные элементы положительны (см. следствие 8.3). Это значит, что диагональная матрица D положительно определена. Следовательно,

при ω < 2 и х ≠ 0. Если ω > 0, то и r > 0. Согласно теореме 11.3, при 0 < ω < 2 итерационная последовательность метода верхней релаксации сходится.

При ω = 1 метод верхней релаксации превращается в метод Зейделя. Из следствия 11.2 сразу получаем следующее утверждение.

Следствие 11.3. Если А — симметрическая положительно определенная матрица, то итерационная последовательность метода Зейделя сходится.

Для метода простой итерации теорема 11.3 дает условие сходимости, более сложное для проверки.

Следствие 11.4. Если А — симметрическая положительно определенная матрица, то итерационная последовательность метода простой итерации сходится при

0 < r < 2/λmах, (11.24)

где λmах — наибольшее собственное значение матрицы А.

Метод простой итерации (11.16) получается из канонической формы (11.22) стационарного метода в случае В = Е. Условие теоремы 11.3 для этого метода имеет вид Е — 0,5rA > 0, r > 0. Матрица Е — 0,5rA симметрическая. Поэтому она положительно определена тогда и только тогда, когда положительны все ее собственные значения (см. 8.6).

Покажем, что каждому собственному значению μ матрицы Е — 0,5rА соответствует собственное значение λ = 2(1-μ)/r матрицы А. Пусть х — собственный вектор матрицы Е — 0,5rA, отвечающий собственному значению μ , т.е. (Е — 0,5rА)х = μx. Тогда х — 0,5rАг = μx, откуда Ах = 2x(1-μ)/r . Следовательно, х — собственный вектор матрицы А, при этом собственное значение равно λ = 2(1-μ)/r. Выразив отсюда μ, находим μ = = 1 — 0,5λ.

Собственное значение μ матрицы Е — 0,5rА положительно, если для соответствующего ему собственного значения λ матрицы А выполняется неравенство 1 — 0,5rλ > 0, или λ < 2/r. Отсюда вытекает, что если максимальное собственное значение λmах матрицы А меньше 2/r, то все собственные значения матрицы Е — 0,5rА положительны и эта матрица является положительно определенной. Согласно теореме 11.3, итерационная последовательность метода простой итерации сходится, если λmах < 2/r.

Условия сходимости типа (11.24) можно получить для произвольного стационарного метода.

Теорема 11.4. Для сходимости итерационной последовательности стационарного метода, заданного канонической формой (11.22), при любом начальном приближении необходимо и достаточно, чтобы все корни характеристического уравнения матрицы Т = Е — rВ^-1А были по модулю меньше единицы. #

Отметим, что в теореме не требуется, чтобы матрица А СЛАУ была симметрической. Достаточно лишь, чтобы и А, и В были невырожденными матрицами. В этом случае харак-теристическое уравнение матрицы Т может иметь как действительные корни (собственные значения), так и комплексные. Для сходимости итерационной последовательности нужно, чтобы все корни, и действительные, и комплексные, по модулю были меньше единицы.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ