Описание итерационных методов

Итерационные методы решения системы линейных алгебраических уравнений (СЛАУ) состоят в построении последовательности столбцов x¹, х², x^N, ... Каждый очередной столбец x^N+1 вычисляется на основе одного или нескольких предыдущих столбцов. Если в итерационном методе столбец x^N+1 вычисляется с использованием одного предшествующего столбца x^N, то такой метод называют одношаговым, в двухшаговых интерационных методах текущий столбец вычисляется с использованием двух предшествующих столбцов. В общем случае, если для вычисления x^N+1 используют столбцы x^N, x^N-1, ..., x^N-k+1 (всего k столбцов), то говорят о k-шаговом итерационном методе. Наиболее употребительны одно- и двухшаговые методы.

Общее представление об одношаговых методах дает метод простой итерации решения нелинейного уравнения f(x) = 0, в котором f(x) — произвольная функция одного действительного переменного [II]. Для применения этого метода нужно уравнение преобразовать к виду х = φ(x). Отправляясь от некоторого начального приближения x₀, строят итерационную последовательность {x_n} согласно формуле x_n+1 = φ(x_N), N = 0,1,2,... Если эта последовательность сходится к некоторому значению x_*, т.е. |x_N — x_*| —> 0 при N —> ∞, а функция φ(x) непрерывна в точке x_*, то, переходя в равенстве x_N+1 = φ(x_N) к пределу при N —> ∞, заключаем, что x_* = φ(х_N) и значение x_* является искомым решением уравнения f(x) = 0. В качестве приближения точного решения x_* берут одно из значений x_N, достаточно близкое к х_*.

Аналогично можно поступить и в случае решения СЛАУ Ах = b с невырожденной матрицей А. Преобразовав СЛАУ в эквивалентную ей систему вида х = Ф(x) = Вх + с, мы можем построить итерационную последовательность x^N+1 = Ф(х^N), N = 0,1,.., начав с некоторого начального столбца х⁰ (индексы в нашем случае удобнее ставить вверху, а не внизу, оставляя нижний индекс для нумерации элементов матриц и столбцов). Сходимость такой последовательности, состоящей из столбцов, или элементов пространства Rⁿ, следует рассматривать относительно некоторой нормы. Последовательность {x^N} сходится к некоторому столбцу x*, если ||х^N — x^*|| —> 0 при N —> ∞. Векторная функция Ф(x) = Вх + с непрерывна в любой точке x^* ∈ Rⁿ, и мы можем перейти к пределу под знаком непрерывной функции: х∞ = Вх∞ + с. Таким образом, предел итерационной последовательности дает нам точное решение СЛАУ, а в качестве приближенного решения системы можно взять подходящий столбец итерационной последовательности.

Каноническая форма одношаговых методов. Наиболее употребительные одношаговые итерационные методы решения СЛАУ укладываются в единую схему, согласно которой итерационная последовательность {х^N}, построенная по такому методу, подчиняется уравнению общего вида

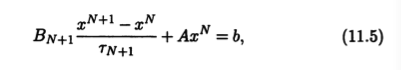
в котором detB_N+1 ≠ О, N = 0,1,...

Уравнение (11.5) называют канонической формой одношагового итерационного метода. Выбор невырожденных матриц B_N+1 характеризует конкретный метод, итерационный параметр Τ_N+1 не является обязательным (его можно было бы учесть в матрице В_N+1) и вводится в уравнение из соображений удобства. Его используют для поиска путей усиления конкретного метода с точки зрения сходимости итерационной последовательности и скорости этой сходимости.

В канонической форме одношагового итерационного метода изменение x^N+1 — x^N текущего столбца фактически связывается с невязкой b — Ax^NN, которую дает этот столбец в рассма-триваемой СЛАУ. Чем меньше невязка, тем меньше изменение текущего столбца. Матрица В_N+1 реализующая эту связь на N-м шаге, должна быть достаточно простой, так как, согласно канонической форме метода, для получения изменения x^N+1 — x^N требуется вычисление обратной матрицы для В_N+1. Если это не так, то более простым может быть обращение матрицы А, и тогда прямой метод решения СЛАУ окажется более предпочтительным.

Если в канонической форме (11.5) одношагового итерационного метода матрица В_N+1 является единичной, то итерационный метод называют явным, а иначе — неявным. Если матрицы B_N+1 и итерационный параметр Τ_N+1 от номера итерации не зависят: B_N+1 = В, Τ_N+1 = Τ, то метод называют стационарным.

Методы Якоби и Зейделя. Представим невырожденную матрицу А в виде суммы трех матриц

А = A_- + D + А₊, (11.6)

где D — диагональная матрица; А_ и А₊ — соответственно нижняя и верхняя треугольные матрицы с нулевыми элемента-ми на диагонали. Такое представление существует и единственно, так как в каждой позиции только одна из складываемых матриц имеет ненулевой элемент, равный соответствующему элементу матрицы А. Матрица А_ содержит элементы А, рас-положенные под главной диагональю, матрица А₊ — элементы над главной диагональю, а м,атрица D — диагональные.

Пример 11.1. Для квадратной матрицы

четвертого порядка в представлении (11.6) имеем

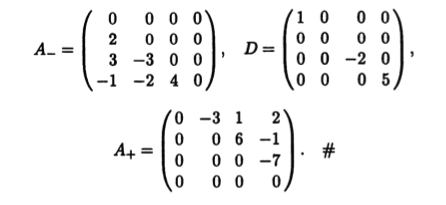
В СЛАУ Ах = b вместо матрицы А подставим ее представление (11.6). Получим (A- + D + A₊)x = Ь, откуда

Dx = -(A_ + A₊)x + b. (11.7)

Если диагональные элементы матрицы А = (а_ij) не равны нулю, то диагональная матрица D = diag(a ₁₁n, a₂₂, ... , a^-1 ) имеет обратную матрицу D^-1 = diag(a^-1₁₁n, a^-1₂₂, ... , a^-1_nn)- этом случае систему (11.7) можно записать в виде

x = -D^-1(A_ + A₊)x + D^-1b. (11.8)

Систему (11.8) можно использовать для построения итерационной последовательности

x^N+1 = -D^-1(A_ + A₊)x^N + D^-1b, N = 0,1,..., (11.9)

где х⁰ — произвольное начальное приближение. Вычисление решения СЛАУ при помощи указанной последовательности называют методом Якоби. Матричные соотношения (11.9) несложно записать в координатной форме. Обозначая номера строк и столбцов индексами внизу, получим

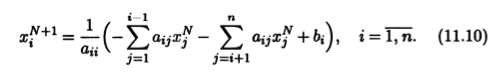
Здесь и далее мы условимся считать равными нулю суммы, у которых верхний предел суммирования меньше нижнего.

Используя представление (11.6) матрицы А, запишем СЛАУ Ах = b в следующем виде:

(D + A_)x = -A₊x + b. (11.11)

Если диагональные элементы матрицы А не равны нулю, то нижняя треугольная матрица D + А_ имеет обратную матрицу (D + А_)^-1 и систему (11.11) эквивалентна следующей:

x = (D + A_)^-1(-A+₊x + b). (11.12)

Соотношение (11.12) можно использовать для построения ите-рационной последовательности

x^N+1 = (D + A_)^-1(-A+₊x^N + b). (11.13)

использование которой для решения СЛАУ Ах = b называют методом Зейделя.

Для вычисления итерационной последовательности в методе Зейделя требуется обращение нижней треугольной матрицы D + А_, но оказывается, Что такое обращение является формальным. Преобразуем соотношение (11.13):

Dx^N+1 = -A_xⁿ⁺¹ - A₊x^N + b.

Исходя из этой формы уравнения, получаем

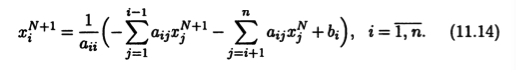
В уравнениях (11.14) элементы хстолбца x^N+1_i находятся и в левой, и в правой части. Однако если их вычислять последовательно для i = 1, i = 2, i = n, мы увидим, что в формуле для очередного элемента х^N+1_i используются только уже найденные элементы x^N+1₁, ..., x^N+1_i-1. Обращение матрицы D + А_ естественным образом встроено в вычислительную схему и не требует отдельных усилий.

Вычислительные схемы методов Зейделя и Якоби, которые описываются уравнениями (11.10) и (11.14), очень похожи. Различие лишь в том, что при вычислении каждого элемента столбца x^N+1 в методе Якоби используются только элементы предыдущего столбца x^N, а в методе Зейделя более новые уже найденные элементы текущего столбца.

И метод Якоби, и метод Зейделя могут быть получены в рамках канонической формы (11.5) одношаговых итерационных методов. Итерационная последовательность метода Якоби подчиняется уравнению Dx^N+1 = — (A_ + A₊)x^N + b, которое эквивалентно (11.9). Это уравнение легко преобразуется в форму Dx^N+1 = —(А — D)x^N + b, откуда получаем

D(x^N+1 - x^N) + Ax^N = b.

Видим, что для получения метода Якоби в канонической форме надо положить В_N+1 = D, Τ_N+1 = 1. Таким образом, метод Якоби можно квалифицировать как одношаговый неявный ста-ционарный итерационный метод.

Из уравнения (11.13) находим (D + A_)x^N+1 = —A + x^N + b, или, заменяя матрицу А₊ через матрицу А, (D + A_)x^N+1 = —(А — D — A_)X^N + b. Следовательно,

(D + A_)(x^N+1 - x^N) + Ax^N = b. (11.15)

Для представления метода Зейделя в канонической форме мы должны положить B_N+1 = D + А_, Τ_N+1 = 1, N = 0,1,... Таким образом, метод Зейделя также относится к одношаговым стационарным неявным методам.

Другие итерационные методы. Полагая в канонической форме итерационных методов B_N+1 = E, Τ_N+1 = Τ, N = 0,1,..., получаем уравнение

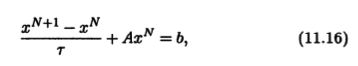
дающее метод простой итерации, представляющий собой явный стационарный метод. Обобщением метода простой итерации является метод Ричардсона, для которого в Описание итерационных методов форме (11.5) итерационных методов следует положить B_N+1 = Е. В результате получим

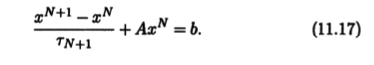
В уравнение (11.15) метода Зейделя введем числовой параметр ω:

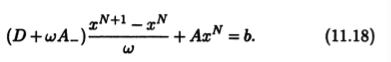
Это приведет к серии методов, среди которых находится и метод Зейделя, соответствующий частному случаю ω = 1. Ско-рость сходимости итерационной последовательности загасит от параметра ω, подбирая который можно получить метод, более точный по сравнению с методом Зейделя. Уравнение (11.18) задает метод верхней релаксации. К нему близок метод нижней релаксации, который имеет уравнение

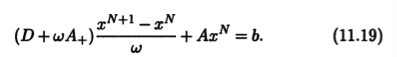
Как и метод Зейделя, методы верхней и нижней релаксации связаны с обращением матрицы, которое естественно встроено в вычислительную схему метода. В случае метода верхней релаксации преобразуем уравнение (11.18) к виду

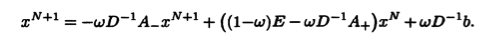
Записывая это уравнение в координатах, находим

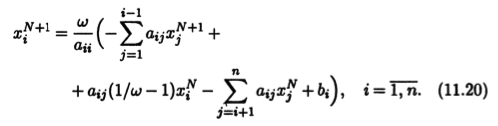
В методе нижней релаксации приведем уравнение (11.19) канонической формы к виду

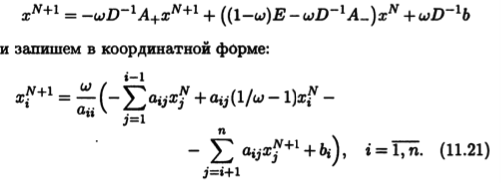
Из (11.20) и (11.21) следует, что методы верхней и нижней релаксации различаются порядком вычислений. В методе верхней релаксации элементы столбца х^N+1 вычисляются последовательно от первого к последнему (как в методе Зейделя), а в методе нижней релаксации, наоборот, — от последнего к первому.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ