QR-разложение. Сингулярное разложение

Одним из вариантов мультипликативного разложения матрицы является QR-разложение, т.е. представление матрицы А в виде А = QP, где Q — ортогональная матрица, a R — верхняя треугольная матрица.

Построение QR-разложения матрицы А сводится к преобразованию этой матрицы путем последовательного умножения на ортогональные матрицы P₁, Р₂, ..., P_s специального вида так, чтобы в результате получилась верхняя треугольная матрица R = P_s...P₁A. Полагая Q = (P_s...P₁)^-1, получаем представление А = QRy где матрица Q, согласно свойствам 7.4 и 7.5 ортогональных матриц (см. с. 200), является ортогональной. 

Применяют два основных способа построения последовательности матриц P₁, ... ,Р_n. Для описания этих способов удобно интерпретировать ортогональные матрицы как матрицы ортогональных операторов в стандартном ортонормированном базисе в Rⁿ, а матрицу А как набор столбцов a₁, ... ,a_n, представляющих собой координаты векторов a₁, ... , а_n из Rⁿ. Тогда ОА = 0(а₁ ... а_n) = (Оа₁ ... Oa_n), где использованы свойства умножения блочных матриц, и поэтому умножение матрицы А слева на ортогональную матрицу О равносильно применению к каждому из векторов а_i ортогонального оператора О, матрицей которого является О. Таким образом, задача сводится к последовательности ортогональных преобразований системы векторов a₁, ..., a_n, в результате которой столбцы координат этой системы образуют верхнюю треугольную матрицу.

Метод вращений. В качестве элементарного ортогонального преобразования рассмотрим преобразование поворота Q_ij(φ) в двумерном подпространстве, образованном i-м и j-м векторами стандартного базиса в Rⁿ (это подпространство естественно ассоциировать с плоскостью). Матрица такого преобразования имеет вид

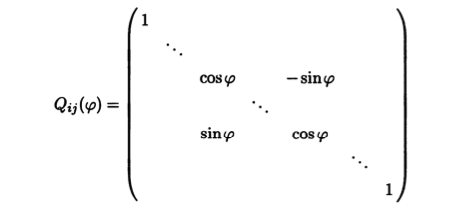
и отличается от единичной элементами на пересечении i-й и j-й строк, i-ro и j-го столбцов. Эти элементы образуют матрицу второго порядка

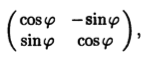
которая на плоскости (в пространстве V₂) определяет поворот вектора на угол φ. Если примененить преобразование с матрицей Q_ij(φ) к произвольному вектору а = (α₁, α_n), то изменятся только его i-я и j-я координаты, а остальные останутся прежними. При этом за счет выбора угла φ можно добиться, чтобы j-я координата вектора обнулилась. Для этого при i < j достаточно выбрать φ из условия

α_isinφ α_jcosφ= 0.

Рассмотрим последовательность преобразовании Q_ij(φ_1j), j = 2,n, в результате которых вектор a₁, представленный первым столбцом матрицы А, превратится в вектор а¹₁ = (а¹₁₁х 0 ... 0)^T . При этом векторы а²,..., аⁿ, представленные остальными столбцами матрицы А, преобразуются в некоторые векторы а¹₂,..., a¹_n с координатами (а¹_1l,..., a¹_nl)^T , l = 2,n. Далее рассмотрим последовательность преобразований Q_2j(φ_2j), j = 3,n, при которой вектор а¹₂ переходит в вектор а²₂ = (а¹₁₂ a²₁₂ 0 ... 0)^T . При этом вектор а¹₁ не изменится, так как преобразуются лишь те координаты, которые у этого вектора равны нулю. Продолжая процесс, мы получим систему векторов a¹₁, ..., aⁿ_n, координаты которых составляют верхнюю треугольную матрицу. Последовательность ортогональных матриц Q_ij(φ_ij), i = 1,n-1, j = i+1,n, и есть искомая последовательность P₁, ..., Р_s.

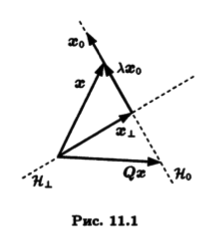
Метод отражений. В этом методе в качестве элементарных ортогональных преобразований берут преобразования симметрии. Рассмотрим произвольный ненулевой вектор х₀ из Rⁿ. Пусть Н^⊥- ортогональное дополнение одномерного линейного подпространства Нv = span{x₀}- Согласно следствию 3.1, каждый вектор х ∈ Rⁿ представляется в виде х = λx₀ + х_⊥, где λx₀ — ортогональная проекция вектора х на Н₀, а х_⊥ — его ортогональная составляющая. Рассмотрим преобразова-ние

Qx = Q(λx₀ + х_⊥) = х_⊥ — λx₀ = х — 2λx₀

(рис. 11.1). Нетрудно показать, что это преобразование является линейным. Кроме того, согласно теореме Пифагора,

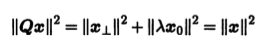
(здесь рассматривается евклидова норма, соответствующая стандартному скалярному произведению в Rⁿ). Поэтому линейный оператор Q является ортогональным.

Лучше всего в качестве вектора x₀ взять вектор n с единичной нормой. Тогда λ = (x, n), а линейный оператор Q записывается в виде

Qx = х — 2(х, n)n, ||n|| = 1.

Линейный оператор Q указанного вида будем называть отражением.

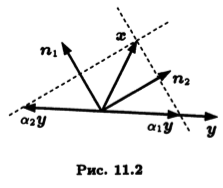
Покажем, что для любых ненулевых векторов x и у из Rⁿ найдется такое отражение О, что Ох = αу, т.е. вектор х преобразуется в вектор, коллинеарный у. Из определения от-ражения следует, что Ох — х = —2(х, n)n. Значит, искомое отражение должно определяться единичным вектором n, коллинеарным вектору Ох — х = αу — х. Отметим, что в этом случае число α определено с точностью до знака, так как ||αу|| = ||Ox|| = ||x|| и, значит, |||| = ||x||/||у||. Выбор знака — это выбор одного из двух возможных решений (рис. 11.2). 

Итак, выбираем α = ||x|| / ||у|| и вычисляем вектор x₀ = αy — х. Бели этот вектор нулевой, то векторы х и у коллинеарны (любой из них принадлежит линейной оболочке другого), и в качестве отражения следует взять тождественный оператор. Если x₀ ≠ 0, то отражение О задается единичным вектором n = х₀/||x₀||. Действительно,

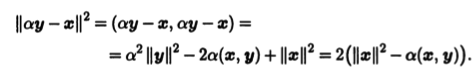
Поэтому

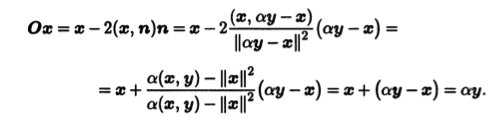
Столбцы матрицы А будем трактовать как столбцы коор-динат некоторых векторов a₁,..., а_n из Rⁿ. Пусть е₁,..., е_n — стандартный ортонормированный базис в Rⁿ. Рассмотрим ортогональное преобразование P₁, которое вектор a₁ переводит в вектор а¹₁ = α₁e₁. Бели вектор ах ненулевой, это преобразование строится описанным выше способом, а если вектор a₁ нулевой, то в качестве Р₁ можно взять тождественный оператор.

Оператор P₁ преобразует векторы а₂, ..., a₂ в некоторые векторы а¹₂, ..., а¹_n. Рассмотрим оператор Р₂, который преобразует вектор а¹₂ = (а¹₁₂а¹₂₂ ... а¹_n2) в некоторый вектор Ра¹₂ = а²₂ = (a²₁₂а²₂₂0 ... 0)^T . Для этого в качестве вектора у можно взять любую линейную комбинацию базисных векторов е₁ и е₂. Некоторая свобода выбора оператора Р₂ позволяет при этом добиться того, чтобы вектор e₁, а значит и а¹₁, не изменялся. Действительно, все векторы, попадающие в ортогональное дополнение Н^⊥, остаются без изменений, и нам достаточно потребовать, чтобы вектор x₀ = Р₂a¹₂ — a¹₂ = αу — а¹₂, задающий отражение Р₂, был ортогонален вектору е₁. Это и будет означать, что вектор е₁ попадает в линейное подпространство которое состоит из всех векторов, ортогональных x₀. Указанное условие будет выполняться, если оператор Р₂ переводит вектор а¹₂ — а¹₁₂е₁ = (0 а¹₂₂ ... a¹_n2) в вектор α₂е₂, так как этот оператор определяется вектором x₀ = α₂е₂— (а¹₂ - a¹₁₂e₁), имеющим нулевую первую координату и потому ортогональным е₂. Итак, оператор Р₂ не изменяет вектор a¹₁, преобразует вектор a¹₂ в вектор a²₂ = (а²₁₂а²₂₂ 0 ... 0) , а векторы aⁱ_j, j = 3,n, в некоторые векторы a²_j.

Продолжая процесс, мы на k-м шаге строим преобразование, которое не меняет базисные векторы е_i, i = 1,k-1, но преобразует вектор a^k-1_k — ^k-1_1ke₁ — ... — a^k-1_k-1,ke_k-1 в некоторый вектор, коллинеарный е_k. Если k-й столбец исходной матрицы оказался нулевым, то и вектор а_k будет нулевым и в процессе преобразований P₁, ..., P_k-1 он останется нулевым. В этом случае в качестве очередного оператора Р_k можно взять тождественный оператор.

Процесс ортогонализации. К QR-разложению непосредственное отношение имеет процесс ортогонализации Грама — Шмидта. Любую квадратную невырожденную матрицу А порядка n можно рассматривать как совокупность столбцов, представляющих собой координаты векторов f₁, ..., f_n в некотором фиксированном базисе n-мерного евклидова пространства Ε.

Так как матрица А невырождена, ее столбцы линейно неза-висимы, поэтому векторы f₁,..., f_n образуют в 6 базис, вообще говоря, неортонормированный. Процесс ортогонализации приводит к новому, уже ортонормированному базису e₁,..., е_n. Характерной особенностью процесса ортогонализации является то, что матрица перехода из нового базиса е к старому b является верхней треугольной. Действительно, из соотношений (3.9) следует, что

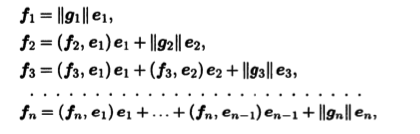
а матрица перехода из нового базиса е в старый f имеет вид

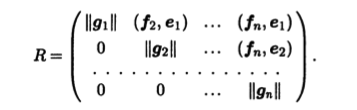
Записав координаты векторов е_j, в фиксированном базисе евклидова пространства, получим ортогональную матрицу Q. Исходная матрица А и ортогональная матрица Q связаны между собой соотношениями А = QR, т.е. мы получили QR-раз-ложение матрицы А.

Еще раз отметим, что процесс ортогонализации Грама — Шмидта может использоваться для получения QR-разложения, если матрица является невырожденной. Кроме того, оказы-вается, что такой метод уступает методу вращений и методу отражений с точки зрения точности вычислений.

Единственность QR-разложения. Несложно привести пример, показывающий, что ^Д-разложение данной матрицы не является однозначным. Действительно, представление Е = ЕЕ единичной матрицы можно рассматривать в качестве ее QR-разложения, так как единичная матрица является одновре-менно ортогональной и верхней треугольной. Но и представление Е = (—Е)(—Е) также является QR-разложением единичной матрицы.

Природу неоднозначности, которую иллюстрирует приве-денный пример, раскрывает следующее рассуждение. Пусть Р — квадратная матрица, которая одновременно является и ортогональной, и верхней треугольной. Тогда Р является невырожденной матрицей, а Р^-1 — ортогональной и верхней треугольной. Поэтому для любого QR-разложения матрицы А имеем А = QR = QPP^-1R = (QP)(P^-1R) = Q'R', т.е. еще одно QR-разложение матрицы А (при Р ≠ Е). Возникает вопрос, какие матрицы являются одновременно ортогональными и верхними треугольными?

Пусть Р — ортогональная верхняя треугольная матрица. Тогда, с одной стороны, Р^-1 = Р^T является нижней треугольной, а с другой стороны Р^-1, будучи обратной к верхней треугольной матрице, является верхней треугольной. Одновременно оба условия выполняются, если матрица Р^-1 является диагональной. Тогда и Р — диагональная матрица. Кроме того, так как РР = РР^T = РР^-1 = Е, то диагональные элементы Р могут иметь лишь два значения 1 и —1.

Используя подходящую диагональную матрицу, у которой на диагонали расположены числа 1 и —1, мы можем любое QR-разложение А = QR матрицы А видоизменить так, чтобы в верхней треугольной матрице А на диагонали стояли неотрицательные элементы. Действительно, надо рассмотреть матрицу Р = diag(p₁, ..., р_n), в которой р_i = 1, если i-й диагональный элемент матрицы R является неотрицательным, и p_i = — 1 в противоположном случае. Тогда А = QR = QP²R = (QP)(PR) = Q'R'и диагональные элементы матрицы R' все неотрицательны.

Теорема 11.2. Бели матрица А невырождена, то ее QA-разложение, в котором диагональные элементы R неотрицательны, определено однозначно.

Отметим, что наличие нулевых диагональных элементов у матрицы R означает, что матрица А вырожденная, а для невырожденной матрицы матрица R в ее QR-разложении не имеет нулевых диагональных элементов.

Пусть А = QR = Q'R'. Так как А невырожденная, то матрица R имеет обратную матрицу. Напомним, что Q ортогональна: Q^TQ = Е. Поэтому равенство QR = Q'R' равносильно следующему: Е = (Q^TQ')(R'R^-1) = ^~Q^~R, т.е. мы получили QR-разложение единичной матрицы. По предположению, диагональные элементы матриц R и R' положительны. Поэтому и верхняя треугольная матрица ^~R имеет положительные диагональные элементы. Таким образом, нам достаточно доказать, что определено однозначно QR-разложение единичной матрицы, т.е. ^~Q = ^~R = Е.

Из равенства ^~Q^~R = Е следует, что ^~R = ^~Q^-1 = ^~Q^T, т.е. верхняя треугольная матрица ^~R является одновременно ортогональной. Поэтому она диагональная (см. выше), а ее диагональные элементы равны ±1. Учитывая, что все диагональные элементы ^~R положительные, заключаем, что ^~R = Е. Но тогда и ^~Q = ^~Q^T = ^~R = E.

Сингулярное разложение. Рассмотрим произвольный оператор А в евклидовом пространстве Ε. Оператор А* А (A* — оператор, сопряженный к А) является самосопряженным, так как для любых векторов х, у ∈ Ε ,

(А* Ах, у) = (Ах, Ау) = (х, А*Ау).

Согласно теореме 6.6, в Ε существует ортонормированный базис b = (b₁ ... b_n) из собственных векторов оператора А* А. Пусть λ₁, ..., λ_n — собственные значения этого оператора, соответствующие векторам b₁,..., b_n, т.е. A* Ab_i = i, i = 1,n.

Отметим, что все собственные значения А* неотрицательны, так как

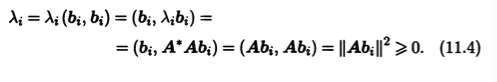
Будем считать, что векторы в базисе b упорядочены таким образом, что последовательтность собственных значений не возрастает. Если среди собственных значений линейного оператора А*А к ненулевых, то λ₁,≥ ... λ_k > 0 и λ_k+1 = ... = λ_n = 0. Положительные числа μ_i = √λ_i, i = 1,k, А:, квадраты которых являются собственными значениями линейного оператора А* А, называют сингулярными числами линейного оператора А, а базис b из собственных векторов А* А — сингулярным базисом оператора А.

Рассмотрим систему векторов c_i = Ab_i,i = 1,k. Эта система состоит из ненулевых попарно ортогональных векторов, так как, согласно (11.4),

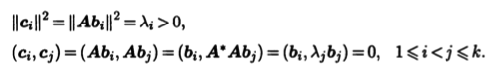
Видим, что нормы векторов с_i равны соответствующим сингулярным числам μ_i линейного оператора А. Положим е_i = μ^-1_ic_i, i = 1,k, и дополним систему векторов e₁, ..., е_k векторами e_k+1, ..., е_n до ортонормированного базиса е в евклидовом пространстве Ε. Пусть Q — линейный оператор, который каждому вектору b_i сопоставляет вектор е_i, т.е. Qb_i = e_i, i = 1,n. Этот линейный оператор определен однозначно, потому что заданы образы всех векторов базиса b. Так как он переводит ортонормированный базис b в ортонормированный базис е, то является ортогональным (см. теорему 7.3). Рассмотрим линейный оператор S = AQ^-1. Если i = 1,k, то

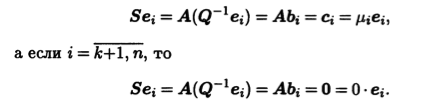
Таким образом, базис e является ортонормированным базисом собственных векторов оператора S. Значит, этот оператор самосопряженный, так как его матрица в базисе е является диагональной (см. теоремы 5.6 и 6.2) и имеет вид D = diag(μ₁, ..., μ_k 0, ..., 0). Обратим внимание, что ненулевые элементы матрицы D — это сингулярные числа линейного опре- атора А.

Из приведенного рассуждения вытекает, что любой линейный оператор А в евклидовом пространстве может быть представлен в виде SQ, где S — самосопряженный линейный опе-ратор с неотрицательными собственными значениями, a Q — ортогональный линейный оператор. Выясним, что это означает для матриц.

Любая матрица А порядка n является матрицей некоторого линейного оператора А в n-мерном евклидовом пространстве Ε. Представление А = SQ этого линейного оператора означает, что для матрицы А имеет место мультипликативное разложение А = SQ, где матрица S симметрическая с неотрицательными собственными значениями, а матрица Q ортогональная. Такое представление называют полярным разложением матрицы А.

Пусть А = SQ — полярное разложение матрицы А. Так как матрица S является симметрической и имеет неотрицательные собственные значения, существует такая ортогональная матрица Р и такая диагональная матрица D с неотрицатель-ными диагональными элементами, что S = Р^TDP (см. теорему 7.7). В результате получаем мультипликативное разложение А = P^TD(PQ) = ^~PD^~Q, где ^~Р и ^~Q — ортогональные матрицы. Это представление не является единственным: несложно заметить, что есть и другие разложения, отличающиеся от указанного порядком диагональных элементов в матрице D.

Пусть А = PDQ, где Р, Q — ортогональные матрицы, а диагональные элементы матрицы D неотрицательны. Тогда

А^TА = (PDQ)^T(PDQ) = Q^TDP^TPDQ = Q^TD²Q.

Полученное равенство означает, что А^TА и D² представляют собой матрицы одного и того же линейного оператора А* А, записанные в двух различных ортонормированных базисах, причем матрица Q — это матрица перехода из базиса, соответствующего матрице D² линейного onpeaтopa, в другой базис, в котором матрицей оператора является А^TА. Матрицей обратного перехода, при котором матрица А^TА самосопряженного линейного оператора А*А преобразуется к диагональному виду D², т.е. перехода к базису из собственных векторов А*А, является матрица Q^-1 = Q^T. Диагональные элементы матрицы D² представляют собой собственные значения оператора А*А, или, что то же самое, собственные значения матрицы А^TА. Количество ненулевых диагональных элементов матрицы D равно рангу матрицы А^TА и совпадает с рангом матрицы А. Дей-ствительно, если Ь=(Ь\ ... Ьп) — базис, в котором линейный оператор А*А имеет матрицу D², то, согласно сказанному выше, векторы Аb_i попарно ортогональны, а поэтому количество ненулевых среди них равно рангу линейного оператора А. Но это количество равно количеству ненулевых диагональных элементов матрицы D². Отметим, что ненулевые диагональные элементы матрицы D представляют собой сингулярные числа оператора А.

Мультипликативное разложение А = PDQ, где Р и Q — ортогональные матрицы, D = diag(μ₁,...,μ_n) — диагональная матрица с неотрицательными диагональными элементами μ₁≥ ... ≥ μ_n, называют сингулярным разложением матрицы А, а диагональные элементы μ₁, ..., μ_n — сингулярными числами матрицы А. Можно показать, что указанное разложение определено однозначно, если матрица А невырождена.

Из приведенных рассуждений вытекает следующая последо-вательность построения сингулярного разложения для невырожденной матрицы:

а) находим собственные числа λ₁,..., λ_n и ортонормированный базис из собственных векторов матрицы А^TА, располагая собственные значения в порядке убывания;

б) строим матрицу D = diag(μ₁,...,μ_n), где μ_i = √μ₁, i = 1,n;

в) составляем матрицу Q^T, записывая в нее по столбцам координаты найденных собственных векторов матрицы А^TА и определяем обратную матрицу Q^-1 = Q^T;

г) находим вторую ортогональную матрицу Р по формуле P = AQ^TD^-1

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ