Операции с тензорами

Линейные операции. Мы видели, что множество полилинейных форм одного типа образует линейное пространство относительно обычных операций сложения функций и умножения функции на число. Каждой полилинейной форме соответствует тензор, и, наоборот, любой тензор можно реализовать как полилинейную форму. Значит структуру линейного про-странства с множества полилинейных форм можно перенести на тензоры.

Определение 10.6. Суммой двух тензоров А = aj1...jqi1...ip и В = bj1...jqi1...ip типа (p,q) называют тензор С = А + В = cj1...jqi1...ip того же типа с компонентами

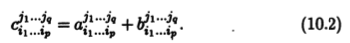
Нетрудно убедиться, что набор компонентов cj1...jqi1...ip, вычисляемых в каждом базисе по формуле (10.2), определяет тензор типа (p,q). Действительно, для двух базисов, старого b и нового с, с матрицей перехода U = (uij) и матрицей обратного перехода V = (vij)

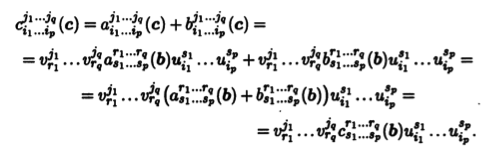
Видно, что набор компонентов сj1...jqi1...ip преобразуется по тензорvному закону, т.е. согласно формуле (10.2).

Введенная операция сложения тензоров одного типа согласуется с операциями сложения объектов, являющихся частными случаями тензоров. Для векторов тензорное сложение совпадает со сложением векторов, для линейных или билинейных форм тензорное сложение равносильно сложению функций. Наконец, тензорное сложение линейных операторов и их обычное сложение — одно и то же. Для полилинейных форм тензорное сложение означает сложение форм как функций.

Определение 10.7. Произведением тензора А = аj1...jqi1...ip нa действительное число λ называют тензор λA с компонентами λаj1...jqi1...ip.

Так же как и в случае сложения тензоров, убеждаемся, что в результате умножения каждой компоненты тензора на число Л мы получаем тензор того же типа. Умножение тензора на число в частных случаях сводится к умножению на число вектора, линейной или билинейной формы, линейного оператора. В интерпретации тензора как полилинейной формы умножение тензора на число равносильно умножению функции на число.

Теорема 10.4. Множество Τ_pq всех тензоров типа (р,q) в n-мерном линейном пространстве L относительно операций сложения тензоров и умножения тензора на число является линейным пространством размерности n^p+q.

Проверка аксиом линейного пространства не представляет сложности. Докажем утверждение о размерности пространства тензоров. Для каждого возможного набора индексов ковариантных i1, ..., ip и контравариантных j1, ..., jq рассмотрим тензор Тi1...iqj1...jp с компонентами (ti1...iqj1...jp)l1...lqk1...kp причем равны нулю все компоненты, кроме одной, индексы которой совпадают с индексами тензора:(ti1...iqj1...jp)j1...jqi1...ip = 1. Тогда любой тензор А = aj1...jqi1...ip представляется в виде линейной комбинации указанных тензоров:

A = aj1...jqi1...ipTi1...iqj1...jp

Докажем, что набор тензоров Ti1...iqj1...jp образует линейно независимую систему. Возьмем линейную комбинацию этих тен-зоров и приравняем нулевому тензору, у которого все компоненты равны нулю: αj1...jqi1...ipTi1...iqj1...jp = Θ. В левой части равенствастоит тензор, компонентами которого являются коэффициенты αj1...jqi1...ip линейной комбинации. Так как этот тензор является нулевым, все его компоненты, они же коэффициенты линейной комбинации, равны нулю. Итак, из равенства нулю линейной комбинации следует равенство нулю ее коэффициентов» Значит, выбранная система тензоров линейно независима и является базисом в пространстве Τp,q . Подсчитаем количество тензоров в построенном базисе. Для этого необходимо опреде-лить количество всевозможных комбинаций из p + q индексов. Так как индексы меняются независимо друг от друга и каждый индекс может иметь п возможных значений, то суммарное ко-личество индексных комбинаций равно тn+q Следовательно, и базис Ti1...iqj1...jp содержит np+q элементов, что равно размерности пространства Τp,q.

Транспонирование. У полилинейной формы можно переставить какие-либо два аргумента одного типа (два вектора или два ковектора). В результате мы получим, вообще говоря, новую полилинейную форму. Например, при перестановке аргументов билинейной формы мы получаем новую билинейную форму, матрица которой является транспонированной к матрице исходной формы. Такая операция не меняет билинейную форму лишь в случае, когда эта форма симметрическая. Транспонирование матрицы в тензорной записи выглядит как перестановка местами индексов, указывающих номер строки и номер столбца.

Определение 10.8. Тензор В = bj1...jqi1...ip полученный из тензора А = aj1...jqi1...ip перестановкой двух первых нижних индексов:

bj1...jqi1i2...ip = aj1...jqi1i2...ip

называют транспонированным к тензору А. Транспонированными называют также тензоры, полученные перестановкой любой другой пары верхних или нижних индексов.

Нужно, естественно, убедиться, что если мы переставляем два верхних или два нижних индекса, то в результате получаем набор компонент, меняющихся при замене базиса по тензорному закону (10.1). При изменении порядка индексов набор компонент тензора в данном базисе остается неизменным, но меняется порядок этих компонент. Например, компоненты тензора валентности 2 можно записать в матрицу. Тогда транспонирование тензора будет означать транспонирование матрицы. Но то же происходит и в общем случае. Компоненты тензора валентности р + q можно рассматривать как элементы (р + q)-мерной матрицы (при р + q = 2 это обычная матрица, ассоциирующаяся с квадратом, при р + q = 3 компоненты матрицы записываются в ячейки куба и т.д.). Если фиксировать все индексы, кроме двух переставляемых, мы получим в многомерной матрице плоское сечение, представляющее собой обычную матрицу. Транспонирование тензора есть транспонирование каждого такого сечения.

Перестановка в тензоре одного верхнего и одного нижнего индекса не имеет какого-либо содержательного смысла, так как при этом нарушается тензорный закон изменения компонент. Это лучше всего наблюдать на простых тензорах типа (1,1) : наличие дополнительных индексов усложняет выкладки, но не дает принципиальных изменений. Тензор типа (1,1) будем трактовать как линейный оператор. Тогда перестановка индексов в компонентах матрицы оператора означает транспонирование этой матрицы. Но транспонирование матрицы линейного оператора в разных базисах приводит к разным операторам. Чтобы такая операция была законной, нужно ограничиться рассмотрением только евклидова пространства и ортонормированных базисов в нем. В этом случае транспонирование матрицы означает переход к сопряженному оператору.

Операцию транспонирования можно усложнить, повторяя ее с разными парами индексов. Пусть, например, среди верхних индексов выбрана группа из s индексов. Используя различные перестановки в этой группе индексов, мы можем расставить эти s индексов в любом порядке. Количество вариантов есть количество перестановок из s элементов, которое равно s! [1-2.6], [III]. Операцию множественной перестановки индексов мы также будем называть транспонированием, выделяя элементарное транспонирование, заключающееся в перестановке пары индексов.

Определение 10.9. Тензор называют симметрическим по группе индексов, если он не изменяется при любой перестановке в этой группе индексов. Тензор кососимметрический по группе индексов (антисимметрический по группе индексов), если при перестановке любой пары индексов из группы он меняет знак.

Особый интерес в связи с этим определением представляют ковариантные и контравариантные тензоры. Симметрический тензор — это ковариантный (контравариантный) тензор, симметрический по группе всех индексов. Аналогично понятие кососимметрического тензора, относящееся к ковариантным или контравариантным тензорам.

Симметрирование и альтернирование. Рассмотрим группу из r верхних (нижних) индексов у тензора А типа (р,q), где r ≤ q (r ≤ р). Перестановкой этой группы индексов можно получить r! тензоров Аδ, включая исходный. Умножим сумму всех этих тензоров на число 1/r! Мы получим новый тензор A^s:

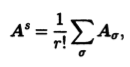
который будет симметрическим по выделенной группе из г индексов. Описанную операцию преобразования тензора, в результате которой получается тензор, симметрический по группе индексов, называют симметрированием.

В частном случае пары индексов симметрирование выглядит наиболее просто. Например, для тензора a_ij симметрирование состоит в получении нового симметрического тензора

(a^s)_ij — (a^s)_ji = 1/2(a_ij + a_ji).

Существует также операция, которая позволяет из данного тензора получить тензор, кососимметрический по группе индексов. Рассмотрим группу из s верхних (нижних) индексов. Любой тензор А_σ, получаемый из тензора А перестановкой этих индексов, можно описать перестановкой σ = (i₁, ..., i_s) из s элементов, причем исходному тензору будет соответствовать тождественная перестановка (1, 2, ..., s). Обозначим через |σ| количество инверсий в перестановке σ[III] и рассмотрим сумму

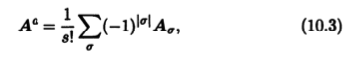
которая берется по всем перестановкам σ из s элементов. Операцию преобразования А —> А^a называют альтернированием по указанной группе индексов. В результате альтернирования тензора получается тензор, кососимметрический по группе индексов. Действительно, перестановка двух индексов в группе меняет четность каждой перестановки σ в сумме (10.3). Значит, каждое слагаемое и вся сумма в целом меняют знак.

В случае тензора a_ij типа (2,0) альтернирование выглядит наиболее просто:

(a^a)_ij — (a^a)_ji = 1/2(a_ij - a_ji).

Произведение тензоров. Две полилинейные формы можно перемножить, образуя функцию от большего числа переменных. Например, из полилинейных форм φ(x₁,..., х_p; f¹,..., f^q) и ψ(y₁,..., y_r; g¹,..., g^s)типов (p,q) и (r,s) можно образовать новую полилинейную форму

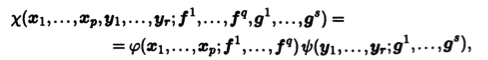
имеющую тип (р+г, q+s). Аналогичная операция существует и для тензоров.

Определение 10.10. Произведением двух тензоров А = aj1...jqi1 ...ip и В = bl1...lqk1 ...kp типов (p,q) и (r,s) называют тензор С = А В типа (p + r,q + s) с компонентами

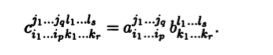
Необходимо, конечно, убедиться, что указанный набор компонент действительно представляет собой тензор, т.е. меняется при замене базиса по тензорному закону (10.1). Непосредственная проверка закона изменения достаточно сложна. Можно ее обойти следующим образом. Каждый тензор можно трактовать как полилинейную форму такого же типа. При этом произведению тензоров будет соответствовать произведение полилинейных форм, так как компонентам перемножаемых тензоров будут соответствовать координаты полилинейных форм, т.е. значения этих форм на различных комбинациях базисных векторов. Убедиться же в том, что при перемножении полилинейных форм получается полилинейная форма, несложно.

Произведение тензоров не является коммутативным. Действительно, при перестановке сомножителей меняется порядок индексов в их произведении. А это ведет к изменению резуль-тата. Чтобы проанализировать ситуацию подробнее, можно рассмотреть произведение двух ковекторов А = а_i, и В = b_j. Их тензорным произведением будет ковариантный тензор С = с_ij ранга 2 с компонентами c_ij= a_ib_j. Если изменить порядок сомножителей, то получим c'_ij = b_ia_j = c_ji, т.е. тензор С', транспонированный к тензору С. Тензоры С и С' совпадают, если каждый из них является симметрическим. Например, если

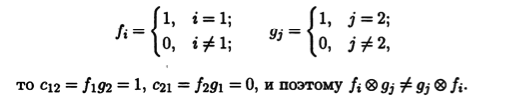
Умножение тензоров является ассоциативным и дистрибутивным по отношению к сложению. Это напоминает свойства умножения линейных операторов. Однако отметим, что про-изведением двух линейных операторов является линейный оператор, а их произведением как тензоров является тензор типа (2,2) , который трактовать как линейный оператор нельзя. Эти две операции принципиально разные, хотя и обладают некоторыми одинаковыми алгебраическими свойствами.

Произведение тензоров открывает возможность получать новые тензоры из тензоров более низкой валентности. Отталкиваясь от векторов и ковекторов, мы можем получать тензоры любого типа. Однако не каждый тензор может быть представлен в виде произведения тензоров. Например, билинейная форма, являющаяся произведением двух ковекторов, имеет матрицу специального вида, ранг которой равен единице. В качестве контрпримера достаточно взять билинейную форму с рангом, равным 2.

Оказывается, что любой тензор типа (р, q) может быть представлен в виде линейной комбинации элементарных тензоров вида х1 ... хp y1 ... уq, являющихся произведением р ковекторов хi и q векторов yqj. Действительно, вспомним базис в пространстве Τp,q тензоров типа (p,q), рассмотренный в доказательстве теоремы 10.4. Каждый из тензоров этого базиса является элементарным. Тензор Ti1...iqj1 ...jp, у которого единичное значение имеет компонента с индексами нижними i1,..., ip и верхними j1,..., jq, является произведением

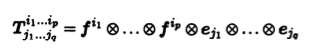
векторов базиса (e1 ... еn) и ковекторов двойственного ему базиса (f1 ... fn). Поэтому любой тензор А = aj1...jqi1 ...ip представим в виде

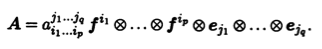
Свертывание. Бели тензорное умножение позволяет полу-чать тензоры более высокой валентности, то следующая опера-ция, наоборот, понижает валентность тензора.

Определение 10.11. Сверткой тензора А = аj1...jqi1 ...ip типа (p,q) по одному верхнему и одному нижнему индексам, например по индексам i1 и j1, называют тензор В = bj2...jqi2 ...ip типа (р — 1,q — 1) с компонентами

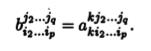
Напомним, что наличие одинаковых верхнего и нижнего индексов предусматривает суммирование по этому индексу (правило индексов). Можно убедиться, что введенная операция приводит к тензору, т.е. для нового набора компонент остается верным закон (10.1) преобразования тензоров.

Пример 10.11. Сверткой тензора типа (1,1) является тензор валентности 0, т.е. инвариант. Тензор типа (1,1) представляет собой совокупность элементов матрицы линейного оператора, а его свертка — это сумма диагональных элементов матрицы оператора, т.е. не что иное, как след матрицы линейного оператора, который от выбора базиса не зависит. #

Говорят также о свертке двух тензоров, подразумевая под этим свертку произведения этих тензоров, причем один из двух индексов, по которым выполняется свертка, относится к первому тензору, а второй — ко второму. Например, выражение а^k_ijb^rs_k означает свертку тензоров А типа (2,1) и В типа (1,2), в результате которой получается тензор типа (2,2).

Свертка тензора или двух тензоров может выполняться не по одной паре индексов, а по нескольким. Например, рассмотрим тензор а^j_i типа (1,1). Произведением этого тензора на себя будет тензор а^j_iа^l_k типа (2,2). Это произведение можно свернуть по двум парам индексов. Получим инвариант (тензор типа (0,0)) a^j_iaⁱ_j, который называют инвариантом второго порядка, в отличие от инварианта первого порядка — следа динейного оператора. Отметим, что другой вариант свертки по двум парам индексов aⁱ_ia^j_j, дает квадрат инварианта первого порядка.

В евклидовом пространстве выделен ковариантный метрический тензор g_ij и контравариантный метрический тензор дгК. Свертка тензора А типа (р,д) с g^ij приводит к тензору типа (р + 1,q — 1) и представляет собой операцию опускания индекса тензора, а свертка А с g^ij приводит к тензору типа (р — 1,q + 1), т.е. к поднятию индекса тензора. Компоненты метрического тензора в ортонормированном базисе составляют единичную матрицу. Поэтому в таком базисе опускание (поднятие) индекса выглядит как простая перестановка индекса сверху вниз (снизу вверх), т.е. различие между верхними и нижними индексами исчезает. Если рассматривается евклидово пространство и в нем только ортонормированные базисы, то все индексы можно записывать или только вверху, или только внизу. Возникающий при этом объект называют евклидовым тензором.

Поливекторы. Поливекторами {мультивекторами) называют ковариантные и контравариантные кососимметри-ческие тензоры. Контравариантный кососимметрический тензор типа (О,q) называют также q-вектором, а ковариантный кососимметрический тензор типа (р, 0) — р-формой. В частном случае 2-форма, т.е. кососимметрический тензор типа (2,0), представляет собой кососимметрическую билинейную форму с кососимметрической матрицей.

Легко проверить, что множество поливекторов одного типа, например (р,0), образуют относительно сложения тензоров и умножения тензора на число линейное пространство. Это линейное пространство является линейным подпространством в пространстве Τ_p,0 всех тензоров типа (р,0).

Компоненты кососимметрического тензора, имеющие хотя бы одну пару одинаковых индесов, равны нулю, так как, с одной стороны, при перестановке этих индексов соответствующая компонента меняется на компоненту с противоположным знаком в силу условия кососимметричности, а с другой стороны, перестановка одинаковых индексов не приводит к изменению компоненты. Значит, валентность ненулевого поливектора не может превышать размерности n линейного пространства, поскольку у тензора валентности больше n любая компонента имеет одинаковые индексы.

У кососимметрического тензора валентности n, где n — размерность линейного пространства, имеется n! ненулевых компонент. Например, для ковариантного кососимметрического тензора компонента а_i1...in отлична от нуля, если все индексы различны, а все такие комбинации индексов получаются при помощи перестановок порядка n. Все ненулевые компоненты такого тензора различаются лишь знаком, так как получаются друг из друга перестановкой индексов. В частности, отсюда следует, что любые два ненулевых кососимметрических тензора валентности n одного типа могут быть получены друг из друга умножением на число. Это означает, что линейное пространство n-векторов (n-форм) является одномерным.

Итак, у любого кососимметрического тензора имеются компоненты, которые различаются лишь знаком или совпадают. Чтобы определить тензор, достаточно указать те компоненты, у которых индексы упорядочены, например, по возрастанию. Все остальные компоненты можно получить при помощи перестановки индексов. Таких ведущих компонент у кососимметрического тензора валентности р имеется С_n^p = n!/p!(n-p)!. Нетрудно увидеть, что у тензоров валентностей р и n - р одинаковое количество ведущих компонент. Рассмотрим, например, р-вектор с компонентами а^j₁...j_p, j₁ < ... < j_p. Каждой компоненте а^j₁...j_n-p сопоставим равное ей число b^r₁...r_p, взяв в качестве индексов r₁ < ... < r_n-p те, которых нет среди индексов j₁, ..., j_p. Можно показать, что в результате мы получим набор компонент кососимметрического (n—р)-вектора, соответствие не зависит от выбора базиса и является изомор-физмом линейных пространств р-векторов и (n—р)-векторов. Аналогичный изоморфизм существует для пространств q-форм и (n-q)-форм.

Произведение кососимметрических тензоров, вообще гово-ря, не является кососимметрическим тензором. Например, произведение АВ кососимметрического тензора А типа (р,0) на кососимметрический тензор В типа (r, 0) будет тензором типа (р+r, 0), который является кососимметрическим по первым р индексам и по последним r индексам, но не по всем индексам вместе. Чтобы получить кососимметрический тензор, нужно выполнить операцию альтернирования по всем индексам. В результате получится кососимметрический тензор С типа (р + r,0), который обозначают АΛВ и называют внешним произведением тензоров А и В.

Пример 10.12. Внешнее произведение двух векторов х = (x₁, x₂,x₃) и у = (у₁, у₂, y₃) в R³ представляет собой кососимметрический 2-вектор с ведущими компонентами

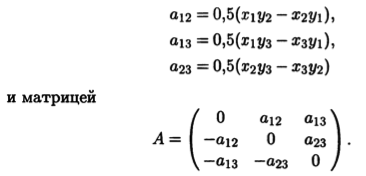
Положив b₁ = 2а₂₃, b₂ = — 2а₁₃, b₃ = 2a₁₂, получим вектор, который совпадает с векторным произведением х×у.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ