Тензоры

Определение 10.4. Говорят, что в n-мерном линейном пространстве L задан тензор типа (р,q)*, если каждому базису Ь в L сопоставлена упорядоченная система чисел аj1...jqi1...ip(b), называемых компонентами тензора, причем системы чисел, соответствующие разным базисам Ь и с, связаны между собой соотношениями

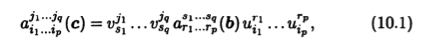
где U = (uⁱ_j) — матрица перехода из базиса b в базис с; V = (vⁱ_j) — обратная к U матрица (верхний индекс у uⁱ_j и vⁱ_j обозначает номер строки в матрице). Сумму p + q называют валентностью тензора (или его рангом).

Понятие тензора носит абстрактный характер: происхождение групп чисел, формирующих тензор, не играет роли.

Пример тензора типа (р,q) дают координаты полилинейной формы типа (р,q). Действительно, закон преобразования по-лилинейных форм при замене базиса (см. теорему 10.3) и закон преобразования тензоров того же типа (см. определение 10.4) совпадают. Верно и обратное: любой тензор можно интерпретировать как совокупность координат некоторой полилинейной формы. Если тензору типа (р,q) с компонентами аj1...jqi1...ip(b) в базисе Ь сопоставить полилинейную форму с координатами аj1...jqi1...ip (b) в том же базисе, то в силу совпадения формул преобразования и в любом другом базисе компоненты тензора будут совпадать с координатами полилинейной формы. Эти соображения показывают, что тензоры при необходимости можно трактовать как полилинейные формы и наоборот.

Исходя из определения 10.4 можно предположить, что р > 0 и q > 0. Но это необязательно. Например, если р = 0, то в законе преобразования 10.1 не будет использоваться матрица U, а если q = 0, то не будет использоваться V.

Определение 10.5. Тензор типа (р,0) называют ковариантным, а тензор типа (0,д) — контправариантным. Тензор типа (р,q) смешанный, если р > 0, q > 0. Про такой тензор говорят, что он р раз ковариантный и q раз контрава- риантный.

Приведем простейшие примеры тензоров.

Пример 10.5. Допустима ситуация, когда р = q = 0. Это означает, что объект описывается одним числом (индексов нет), причем это число не зависит от выбора базиса (в законе преобразования нет суммирования и он приобретает вид а(с) = а(b)). Такой объект представляет собой тензор типа (0,0). Его также называют инвариантом. Можно также сказать, что инвариант — это попросту скалярная величина.

Пример 10.6. Тензор образуют координаты вектора. Это вытекает из интерпретации вектора как полилинейной формы типа (0,1) (см. пример 10.1). Проверим непосредственно, что координаты вектора представляют собой тензор типа (0,1). Если U — матрица перехода из старого базиса в новый, а V — обратная к U, то столбец ^∽х новых координат вектора х связан со столбцом х старых координат соотношением ^∽х = Vx, а в тензорной записи это выглядит следующим образом: x^∽j = v^j_sx^s. Видим, что это преобразование координат совпадает с преобразованием (10.1) при р = 0, q = 1.

Рассуждая аналогичным образом, убеждаемся что ковектор (линейная форма) представляет собой тензор типа (1,0).

Пример 10.7. Линейный оператор А, действующий в линейном пространстве L, можно ассоциировать с полилинейной формой типа (1,1) (см. пример 10.3). Это значит, что линейный оператор можно рассматривать как тензор типа (1,1). Проверим это непосредственно. В данном базисе Ъ линейный оператор описывается своей матрицей А. При переходе в новый базис с матрица А линейного оператора преобразуется в матрицу ^∽А согласно формуле А^-1AU = VAU. Записав матрицы в тензорной форме (верхний индекс соответствует номеру строки в матрице, а нижний — номеру столбца), получим ã^j_i = v^j_sa^s_ru^r_j (см. пример 10.4), т.е. формулу (10.1) при р = 1, q = 1. Значит, элементы матрицы линейного оператора при переходе в другой базис меняются как компоненты тензора типа (1,1).

Пример 10.8. Символ Кронекера — это тензор δⁱ_j типа (1,1), который в любом базисе имеет значения δⁱ_j = 1 для любого i и δⁱ_j = 0, если i ≠ j. Этот тензор соответствует тождественному линейному оператору, так как компоненты символа Кронекера соответствуют элементам единичной матрицы.

Пример 10.9. В евклидовом пространстве Ε заданное скалярное произведение представляет собой билинейную форму, т.е. тензор g_ij типа (2,0). Этот тензор называют ковариантным метрическим тензором. Роль такого тензора (иначе, скалярного произведения) может играть любая симметрическая билинейная форма, порождающая положительно определенную квадратичную форму.

Евклидово пространство Ε изоморфно своему сопряженному Ε*, причем изоморфизм, определяемый скалярным произве-дением, не связан с выбором базиса (см. 10.1). Этот изоморфизм переносит скалярное произведение из Ε в Ε*, порождая тензор g^ij типа (0,2). Этот тензор называют контравариантным метрическим тензором.

Компонентами ковариантного метрического тензора в данном базисе е являются элементы матрицы Грама Г, так как, согласно определению метрического тензора, g_ij = (е_i, e_j). Матрицей контравариантного метрического тензора g'i в е явля-ется матрица, обратная матрице Грама. Действительно, компоненты тензора g^ij — это элементы матрицы Грама Г* в базисе f, взаимном с е. Пусть U — матрица перехода из базиса е в базис f. Тогда f = eU (f и е, как обычно, представляются в виде строк). Матрица Грама Г* для базиса f записывается в виде Г* = f^Tf. Поэтому

Г* = f^Tf = f^TeU = EU = U.

С другой стороны,

Е = f^Tе = (eU)^Te = U^Tе^Tе = U^TГ,

откуда U = (Г^T)^-1 = Г^-1 и Г* = U = Г^-1.

Примеры тензоров можно почерпнуть в механике и физике.

Пример 10.10. Механические свойства твердого тела связаны с его моментами инерции относительно различных осей. Пусть для простоты тело состоит из конечной совокупности материальных точек, например из N точек. Моменты инерции такого тела относительно координатных осей Ox₁, Ox₂, Ох₃ прямоугольной системы координат задаются формулами

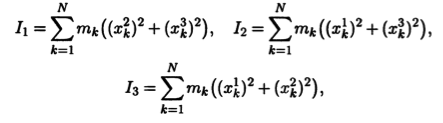
где х¹_k, х²_k х³_k — координаты k-и материальной точки; — масса k-й материальной точки. Если система координат изменилась, мы получим новую тройку моментов инерции, но эта новая тройка не может быть получена из старой при помощи только матрицы перехода, так как в формулы преобразования включаются и центробежные моменты

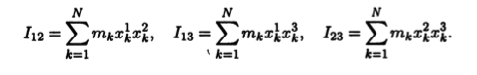
Рассмотрим совокупность чисел

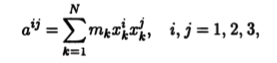
через которые выражаются как моменты инерции (например, I₁ = а²² + а³³), так и центробежные моменты (I_ij = a^ij при i ≠ j). При переходе к новой системе координат О^∽x₁^∽x₂^∽x₃ мы получим новую группу чисел ^∽а^ij , которая связана с исходной группой следующим образом:

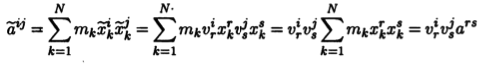
(в выкладке использованы закон ^∽xⁱ = u_rⁱxⁱ преобразования координат радиус-вектора точки и правило суммирования по умолчанию для индексов r и s). Таким образом, группа чисел а^ij представляет собой набор компонент тензора типа (0,2) — тензора инерции.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ