Полилинейные формы

Пусть L — n-мерное линейное пространство и L* — сопряженное к нему пространство. Рассмотрим функцию ψ(x₁,...,x_p; f¹,...,f^q), аргументами которой являются р векторов x_i ∈ L и q ковекторов f^j ∈ L*.

Определение 10.3. Функцию φ от р векторов и q ковекторов называют полилинейной формой, если она линейна по каждому отдельно взятому аргументу. Пару чисел (p,q) называют типом полилинейной формы.

Пример 10.1. Простейшие полилинейные формы — это линейные функции, зависящие от одного аргумента. Линейные функции на L представляют собой ковекторы, т.е. элементы сопряженного пространства L*. Линейные функции на L* отождествляются с векторами. Таким образом, полилинейная форма типа (1,0) — это ковектор, а полилинейная форма типа (0,1) — это вектор.

Пример 10.2. Полилинейная форма типа (2,0) — это билинейная форма, определенная на линейном пространстве L. Аналогично полилинейная форма типа (0,2) представляет собой билинейную форму на сопряженном пространстве L*.

Пример 10.3. Полилинейную форму φ(x;f) типа (1,1) можно ассоциировать с линейным оператором, действующим в линейном пространстве L. Действительно, зафиксировав первый аргумент, мы получим линейную функцию на сопряженном пространстве L*, т.е. вектор. Таким образом, каждому вектору x ∈ L поставлен в соответствие вектор, представленный в виде линейной формы на L*. Мы получаем отображение пространства L в себя. Покажем, что это отображение линейно.

Если вектору x соответствует линейная форма φ(x;•) на L* (точка обозначает меняющийся аргумент), а вектору у соответствует линейная форма φ(y;•), то сумме этих векторов соответствует линейная форма φ(х + у; •), равная сумме форм:

φ(х + у;•) = φ(х;•) + φ(у;•),

что следует из линейности φ по первому аргументу. Аналогично вектору λх соответствует форма φ(λх;•), равная λφ(х;•).

Итак, любой полилинейной форме φ типа (1,1) соответствует линейный оператор, действующий в L. Можно показать, что это соответствие биективное, и мы можем отождествить полилинейные формы типа (1,1) с линейными операторами.

Соответствие между полилинейными формами типа (1,1) и линейными операторами использует ранее построенный изоморфизм между линейными пространствами L и L**. Обратное соответствие более простое. Каждому линейному оператору А можно поставить в соответствие полилинейную форму φ_A(x;f) = (f,Ах) типа (1,1). При фиксированном векторе х мы получаем линейную форму на сопряженном пространстве, причем эта форма отождествляется с вектором Ах. Значит, это действительно то же соответствие, что и рассмотренное выше. #

Полилинейные формы можно складывать по обычным правилам сложения функций: для каждой комбинации значений p + q аргументов складываются значения функций. Полилиней-ные формы можно также умножать на действительные числа.

Теорема 10.2. Множество P_p,q полилинейных форм типа (p,q) в п-мерном линейном пространстве L является линейным пространством относительно обычных операций сложения функций и умножения функции на число.

Операции сложения функций и умножения функции на число удовлетворяют всем аксиомам линейного пространства. Поэтому нам нужно лишь показать, что в результате сложения двух форм одного типа или умножения полилинейной формы на действительное число получается полилинейная форма того же типа.

Рассмотрим полилинейные формы φ(x₁,... ,x_p; f¹,... ,f^q) и ψ(x₁,... ,x_p; f¹,... ,f^q). Их сумма представляет собой функцию χ (x₁,... ,x_p; f¹,... ,f^q), которая определяется равенством

χ(x₁,... ,x_p; f¹,... ,f^q) = φ(x₁,... ,x_p; f¹,... ,f^q) + ψ(x₁,... ,x_p; f¹,... ,f^q)

Проверим линейность этой функции, например, по первому аргументу, используя многоточия для обозначения остальных аргументов полилинейных форм:

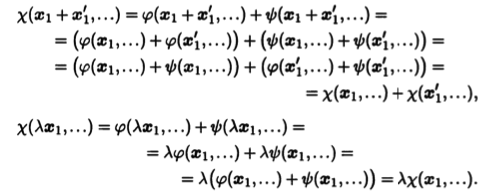
Линейность функции по остальным аргументам проверяется точно так же.

Рассмотрим теперь функцию £, определенную через полилинейную форму (р равенством £(...) = λφ(...). Проверим ее линейность по первому аргументу:

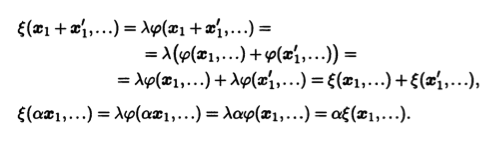
Линейность функции £ по остальным аргументам проверяется аналогично.

Рассмотрим в линейном пространстве L некоторый базис е = (е₁ ... е_n). Используя свойства линейности полилинейной формы φ типа (p,q) по каждому аргументу, мы можем выразить ее значение на фиксированном наборе значений аргументов через ее же значения на базисных векторах. Пусть выбраны произвольные векторы х_i = х¹_iе₁ +... + xⁿ_iе_n, i = 1,p, и произвольные ковекторы fⁱ = fⁱ₁е¹ +... + f¹_nеⁿ, i = 1,q, разложенные по взаимному базису е* = (е¹ ... еⁿ). Тогда

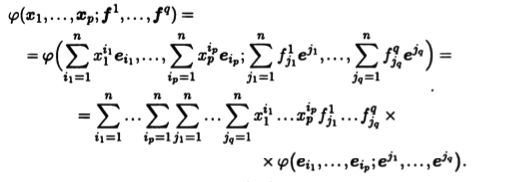
Мы видим, что набор чисел φj1...jqi1...ip = φ(ei1,...,eip;еj1,...,ejq) однозначно задает полилинейную форму. Ясно, что, взяв произвольный набор чисел j1...jqi1...ip мы сможем определить полилинейную форму, используя эти числа как коэффициенты разложения в базисе е. Таким образом, подобно тому, как каждому вектору соответствует столбец его координат, каждой полилинейной форме соответствует набор чисел, упорядоченных с помощью p + q индексов. Эти числа назовем координатами полилинейной формы. Термин оправдан, так как в линейном пространстве Pp,q несложно указать базис, в котором эти числа действительно будут координатами данной полилинейной фор-мы. Этот базис будет состоять из np+q полилинейных форм, и поэтому dimPp,q = пp+q.

Уже по приведенной выкладке видно, что большое количество знаков суммы загромождает вычисления. Поэтому в тензорном исчислении используют правило суммирования по умолчанию, или правило индексов. Индексы в выражениях тензорной алгебры ставят вверху и внизу. Если в выражении какой-либо верхний индекс и какой-либо ниж-ний индекс обозначены одинаково, то подразумевается, что по этому индексу проводится суммирование в пределах от едини-цы до размерности линейного пространства. При этом знак Σ суммирования опускается. Например, формулу разложения полилинейной формы в базисе в соответствии с правилом ин-дексов записывают так:

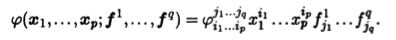
Далее мы будем использовать это правило.

Итак, полилинейную форму в данном базисе можно пред-ставить набором ее координат. Выясним, как изменяются эти координаты при изменении базиса. Пусть b = (b₁ ... b_n) и с = (с₁ ... с_n) — два базиса в n-мерном линейном пространстве L, b* = (b¹ ... bⁿ) и с* = (с¹ ... сⁿ) — базисы в сопряженном пространстве L*, взаимные b и с. Обозначим через U матрицу перехода из базиса b в базис с.

Теорема 10.3. Координаты 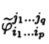полилинейной формы φ в базисе с связаны с координатами φj1...jqi1...ip этой же формы в базисе b соотношениями

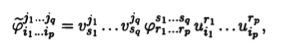
где (uⁱ_j) = U — матрица перехода из базиса b в базис с; (vⁱ_j) = V = U^-1 — матрица обратного перехода (верхний индекс соответствует номеру строки).

Координата 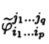, соответствующая фиксированному набору индексов i₁, ...,i_p, j₁, j_q, представляет собой значение полилинейной формы:

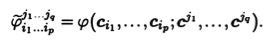
Используя выражение векторов нового базиса через старый при помощи матрицы перехода

c_j = b_ku^k_j, cⁱ = vⁱ_lb^l,

находим

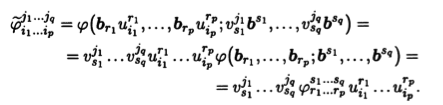
Пример 10.4. Для линейного оператора А с матрицей А = (аⁱ_j), который отождествляется с полилинейной формой типа (1,1) (см. пример 10.3), формула преобразования при переходе к новому базису, согласно теореме 10.3, имеет вид ã^j_i = v^j_sa^s_ru^r_j Эта формула является координатной записью известной формулы А = U^-1AU преобразования матрицы линейного операто-ра (см. теорему 4.6).

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ