Примеры

Описанный выше процесс упрощения уравнения поверхности второго порядка в Rⁿ реализуется и для кривых второго порядка на плоскости, и для поверхностей второго порядка в пространстве [III]. Рассмотрим этот процесс на конкретных примерах.

Пример 9.2. Приведем к каноническому виду уравнение кривой второго порядка

14x²₁ + 24x₁x₂ + 21х²₂ - 4x₁ + 18x₂ - 139 = 0, (9.14)

выпишем все использованные преобразования и построим эту кривую в исходной системе координат.

Квадратичная форма кривой имеет вид 14x²₁ + 24x₁x₂ + 21х²₂, а матрицей этой квадратичной формы является

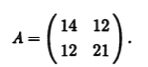
Чтобы найти ортогональное преобразование, приводящее квадратичную форму кривой к каноническому виду, выпишем характеристическое уравнение матрицы А

λ² - 35λ + 150 = 0

и найдем его корни: λ₁ = 30, λ₂ = 5.

Ранг матрицы однородной системы линейных алгебраических уравнений (А - λЕ)х = 0 при λ = λ_1,2 равен единице, и мы можем в системе оставить только одно уравнение - первое: (14 - λ)х₁ + 12x₂ = 0. Собственному значению λ₁ = 30 соответ-ствует единичный собственный вектор

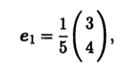
а λ₂ = 5 - единичный собственный вектор

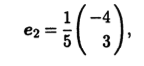
который в двумерном случае проще найти из условия ортогональности вектору e₁, т.е. путем перестановки координат вектора е₁ и изменения знака у одной из координат.

Из найденных координат собственных векторов составляем матрицу ортогонального преобразования

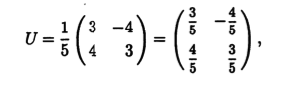
которое является поворотом, так как detU = 1. Этому ортогональному преобразованию соответствует линейная замена переменных

Чтобы получить уравнение кривой с квадратичной формой канонического вида, нужно подставить выражения (9.15) для переменных x₁ и х₂ в (9.14):

Следует отметить, что мы сразу можем записать канонический вид квадратичной формы кривой по известным собствен-ным числам: 30y²₁ + 5у²₂. Линейные слагаемые -4x₁ + 18x₂ = = 2b^Tх, представляющие собой удвоенное скалярное произведение вектора с координатами Ь на вектор с координатами х, в новых переменных будет иметь вид 2(Ub)^Ty - 2b^TUy, или

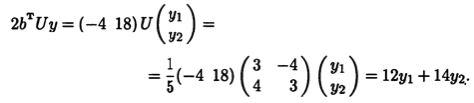
Свободный член в процессе преобразования поворота не изменится. Таким образом, приходим к тому же уравнению (9.16). 

По каждому из переменных выделяем полный квадрат:

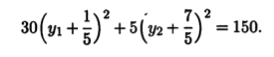
Теперь параллельный перенос системы координат, определяемый соотношениями

приводит к уравнению

30z²₁ + 5z²₂ = 150,

которое легко преобразуется к каноническому уравнению эллипса делением на 150:

z²₁/5 + z²₂/30 = 1.

Чтобы построить эллипс, заданный в исходной системе координат уравнением (9.14), можно поступить следующим образом. Изобразим исходную систему координат Ох₁х₂, а в ней векторы e₁, е₂, которые являются собственными для матрицы квадратичной формы поверхности. Эти векторы откладываем от начала О системы координат, они задают координатные оси новой системы координат Оу₁у₂. В этой системе координат строим точку O₁ (-1/5; -7/5), которая должна быть началом следующей канонической системы координат O₁z₁z₂. Оси этой системы координат параллельны осям Oy₁ и Оу₂.

Определив положение канонической системы координат O₁z₁z₂ относительно исходной Ox₁x₂, строим в ней эллипс, руководствуясь величинами его большой и малой полуосей. В результате получаем расположение эллипса относительно исходной системы координат. Расположение осей трех систем координат и эллипса в данной задаче показано на рис. 9.1. 

Пример 9.3. Определим, какая кривая задается уравнением

32х² + 52x₁x₁ - 7х² ₂+ 180 = 0,

и изобразим ее в канонической системе координат.

Для решения поставленной задачи приведем к канониче-скому виду квадратичную форму F = 32х²₁ + 52x₁x₂ - 7x²₂ этой кривой. Матрица А квадратичной формы имеет вид

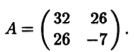
Составим характеристическое уравнение det(A - λЕ) = 0,

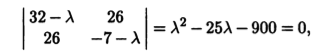
откуда находим собственные значения λ₁ = 45, λ₂ = -20. Теперь мы можем записать канонический вид квадратичной формы кривой:

F = 45у²₁ - 20у²₂-

Так как линейные слагаемые в исходном уравнении отсутствуют, то и после поворота, приводящего квадратичную форму кривой к каноническому виду, линейные слагаемые будут отсутствовать. Свободный член при поворотах также не изменяется. Поэтому в новой системе координат кривая будет описываться уравнением

45у²₁ - 20у²₂ +180 = 0,

или

у²₁/4 - у²₂/9 = -1.

Мы получили уравнение гиперболы, ее положение в канонической системе координат изображено на рис. 9.2.

Пример 9.4. Приведем к каноническому виду уравнение поверхности

4х²₁ + 4х²₂ + х²₃ + 12х₁x₂ - 20 = 0,

определим ее тип и изобразим в канонической системе координат.

Как и в предыдущем примере, уравнение поверхности не содержит линейных слагаемых. Следовательно, чтобы привести уравнение к каноническому виду, достаточно привести к каноническому виду квадратичную форму поверхности. Само преобразование поворота по условию примера находить не требуется.

Квадратичная форма данной поверхности имеет вид

F = 4х²₁ + 4х²₂ + х²₃ + 12х₁x₂.

Запишем ее матрицу

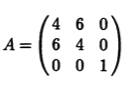
и составим характеристическое уравнение этой матрицы

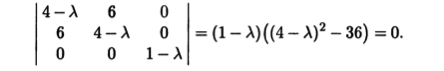
Решая уравнение, находим его корни λ₁ = 1, λ₂ = 10, λ₃ = -2. Зная их, записываем канонический вид квадратичной формы поверхности, а вместе с ним и каноническое уравнение самой поверхности:

у²₁ + 10y²₂- 2у²₃ - 20 = 0,

или

у²₁/20 + у²₂/2 - у²₃/10 = 1.

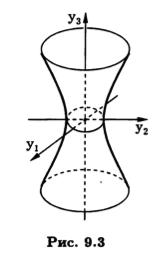
Видим, что полученное уравнение описывает однополостный гиперболоид (рис. 9.3).

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ