Упрощение уравнения поверхности второго порядка

Один из подходов к анализу поверхности второго порядка в Rⁿ, заданной уравнением (9.2), состоит в подборе такой прямоугольной системы координат, в которой уравнение при-нимает наиболее простой вид.

Изменение системы координат приводит к преобразованию исходных координат х точки к ее новым координатам у по формуле

x = Uy + y₀,

где y₀ - координаты начала новой прямоугольной системы координат относительно старой (см. (9.5)), a U - ортогональная матрица. При этом преобразовании уравнение (9.2) трансформируется к виду

(Uy + у₀)^TA(Uу + у₀) + 2b^T(Uy + y₀) + с = 0,

или

y^TU^TAUy + 2(b^TU + y^T₀AU)y + у^T₀Ау₀ + 2b^Tу₀ + с = 0. (9.8)

Уравнение (9.8) показывает, что параллельный перенос системы координат (в этом случае U = Е) не изменяет квадратичной формы поверхности второго порядка. Квадратичная форма поверхности преобразуется по общему правилу (8.4) преобразования квадратичных форм при замене базиса.

Наиболее естественный способ упрощения уравнения (9.2) базируется на предварительном преобразовании квадратичной формы поверхности. Согласно теореме 8.2, существует новый ортонормированный базис, в котором квадратичная форма имеет канонический вид. Этот базис состоит из собственных векторов матрицы А квадратичной формы, записанных в исходном ортонормированном базисе. Матрица перехода от старого ортонормированного базиса к новому ортонормированному базису является ортогональной. Изменяя, если необходимо, направление одного собственного вектора на противоположное, можно считать, что определитель этой ортогональной матрицы положителен и потому равен единице. Значит, существует такой поворот исходной системы координат, что квадратичная форма поверхности (9.2) в новых переменных будет иметь канонический вид.

Пусть y₁ ... y_n - новые координаты, в которых квадратичная форма поверхности (9.2) имеет канонический вид. Начало системы координат при этом не изменяется, и преобразованное уравнение (9.8) поверхности сводится к следующему:

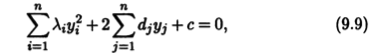
где (d₁ ... d_n)^T = d = U^Tb, а λ_i, i = 1,n, представляют собой собственные значения матрицы А квадратичной формы поверхности, соответствующие векторам нового ортонормиро-ванного базиса. Дальнейшее определяется возможными значениями λ_i и d_i.

Для каждого значения индекса i, i = 1,n, возможен один из четырех случаев:

1) λ_i ≠ 0, d_i ≠ 0;

2) λ_i ≠ 0, d_i = 0;

3) λ_i = 0, d_i ≠ 0;

4) λ_i = 0, d_i = 0.

Если реализуется случай 4), то соответствующая переменная у_i вообще не входит в уравнение и мы имеем случай цилиндрической поверхности в Rⁿ (при n = 3 такая поверхность действительно является цилиндрической [III]). В остальных случаях дальнейшее упрощение уравнения (9.9) сводится к упрощению вида линейных слагаемых.

Если в уравнении (9.9) для i-й переменной y_i реализуется случай 1), то по этой переменной можно выделить полный квадрат:

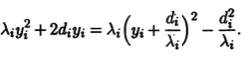
После параллельного переноса системы координат

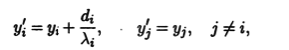
этот случай сводится к случаю 2).

Реализуем все такие параллельные переносы и, если необходимо, изменим порядок переменных (это равносильно перестановке векторов в базисе). Тогда уравнение поверхности (9.9) в новых переменных z примет вид

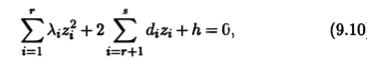
где параметр r определяет количество переменных, для которых реализовался случай 2) (возможно, после выделения полного квадрата и соответствующего параллельного переноса). В остальных случаях реализуется случай 3) (после перестановки индексы от r + 1 до 5) или случай 4) (индексы от s + 1 до n).

Если s = r, то случай 3) не встречается и в уравнении (9.10) линейные слагаемые будут отсутствовать. При s > r +1 случай 3) реализуется для нескольких переменных. Тогда необходим дополнительный поворот, который преобразует ситуацию к случаю s = r + 1. Этот поворот сводится к замене переменных z_r+1, ..., z_s новыми переменными z'_r+1, ..., z'_s, при которой

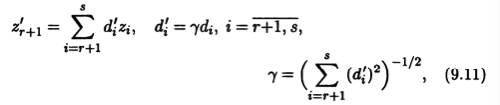
а остальные переменные подбираются так, чтобы соответствующая замена переменных имела ортогональную матрицу U'. Эта матрица при указанной замене переменных имеет блочно-диагональную структуру:

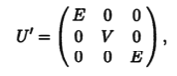
в которой блоки Е представляют собой единичные матрицы порядков r и n - s, а блок V порядка s - r отвечает переменным z_r+1, ..., z_s и должен быть ортогональной матрицей. Элементами первого столбца в этой матрице являются числа d'_r+1, ..., d'_s*. Такую матрицу можно построить, взяв вектор (d'_r+1, ..., d'_s) из (s-r)-мерного линейного арифметического пространства и дополнив его в указанном пространстве до ортонормированного базиса.

Итак, после выделения квадратов и выполнения параллельного переноса мы можем, если нужно, выполнить дополнительный поворот так, что в конечном счете уравнение поверхности (9.2) преобразуется к виду

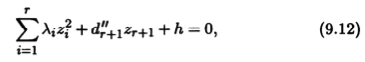
в котором r > 0 (должно быть хотя бы одно слагаемое второго порядка), а коэффициент d"_r+1 может быть нулевым.

Если d"_r+1 ≠ 0 и h ≠ 0, то еще одним параллельным переносом, который определяется заменой переменного z_r+1 по формуле

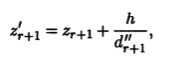
можно "убрать" слагаемое h. Учитывая, что умножение уравнения на произвольное ненулевое число не меняет поверхности, мы заключаем, что исходное уравнение (9.2) путем замены системы координат приводится к одному из следующих видов:

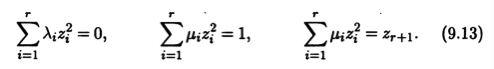
В представлениях (9.13) параметр r является рангом квадратичной формы поверхности второго порядка, который не зависит от выбора системы координат и при описанных пре-образованиях не меняется. В первом и втором случае ранг может иметь любые значения от 1 до n, в последнем случае r < п, т.е. этот случаи возможен для поверхности второго порядка с вырожденной квадратичной формой.

* Равенство (9.11) представляет собой первое из уравнений перехода от нового базиса к старому, которое реализуется обратной матрицей V^-1. Значит, первая строка матрицы V^-1 состоит из коэффициентов в (9.11), но Vv = V^T, т.е. первая строка в V^-1 является первым столбцом в V.

Уравнения (9.13), к одному из которых приводится уравне-ние произвольной поверхности второго порядка в Rⁿ, назовем уравнениями канонического вида, а переменные, в которых они записаны, - каноническими.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ