Изменение системы координат

Пусть даны старая прямоугольная система координат, состоящая из ортонормированного базиса b = (b₁ ... b_n) и ее начала в точке b₀, и новая система координат, состоящая из ортонормированного базиса с = (с₁ ... _n) и начала c₀. Рассмотрим произвольную точку х с координатами х_b и х_c соответственно в старой и новой система-х координат.

Из определения координат точки в Rⁿ имеем соотношения

x - b₀ = bx_b, x - c₀ = cx_c.

Приравнивая выражения для x, получаем

bх_b + b₀ = сx_c + с₀. (9.3)

Пусть U - матрица перехода из ортонормированного базиса b старой системы координат в ортонормированный базис с новой системы координат. Тогда U - ортогональная матрица (см. теорему 7.5) и с = bU. Подставляя это представление для с в равенство (9.3), находим

bх_b + b₀ = bUx_c + с₀,

или

b(х_b - Ux_c) = с₀ - b₀. (9.4)

Координаты вектора c₀ - b₀ относительно базиса b представляют собой координаты точки с₀ (начала новой системы координат) относительно старой системы координат, которые мы обозначим через с_0,b: с₀ - b₀ = bс_0,b. С учетом этого равенства преобразуем правую часть (9.4): b(х_x - Ux_c) = bс_0,b. Отсюда следует, что

x_b = Ux_c + c_0,b. (9.5)

Соотношение (9.5) представляет собой формулу преобразо-вания координат при изменении системы координат.

Если с_0,b = 0, т.е. начала старой и новой систем координат совпадают, то преобразование координат принимает вид

x_b = Ux_c. (9.6)

В двумерном случае при дополнительном условии detU = 1 преобразование (9.6) представляет собой поворот системы координат вокруг неподвижного начала системы координат. В трехмерном случае при том же условии detU = 1 это преобразование является поворотом системы координат вокруг неко-торой оси, проходящей через начало координат. Ось поворота определяется собственным вектором матрицы U с собственным значением 1. Если det U = - 1, то преобразование системы координат кроме поворота включает преобразование симме-трии относительно некоторой плоскости или сводится к одной симметрии.

Пример 9.1. Преобразование системы координат с матрицей

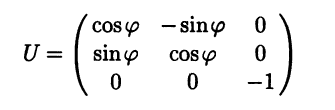
состоит в повороте на угол вокруг третьего вектора исходного базиса и последующей симметрии относительно плоскости, которой параллельны первые два вектора (при повороте эта плоскость перейдет в себя). #

По аналогии с двумерным и трехмерным случаями условно назовем замену (9.6) при произвольном n поворотом системы координат в случае detU = 1 и поворотом системы координат с отражением (симметрией) в случае detU = - 1. Введенные термины условны потому, что в n-мерном пространстве при n > 3 теряется наглядный смысл понятия и "поворот"

Если в преобразовании (9.5) матрица U является единичной, т.е. U = Е, то старая и новая системы координат имеют один и тот же ортонормированный базис. В этом случае преобразо-вание координат имеет вид

x_b = x_c с_0,b. (9.7)

При n = 2,3 такое преобразование означает параллельный перенос системы координат, при котором направления осей координат не изменяются. В общем случае (при n > 3) преобразование (9.7) мы также будем называть параллельным переносом системы координат.

Любое преобразование координат вида (9.5) можно представить как последовательное применение двух преобразований х' = Uх_c и х_b = х' + с_0,b, которые означают параллельный перенос исходной системы координат в точку с и последующий ее поворот (возможно, с отражением), определяемый матрицей U.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ