Поверхности второго порядка

Рассмотрим линейное арифметическое пространство Rⁿ, являющееся евклидовым пространством со стандартным скалярным произведением:

(x, у) = x₁y₁ + x₂y₂ + ... + х_nу_n,

где x = (x₁, ... , х_n), у = (y₁, ..., у_n). Векторы из М3 или R2 можно рассматривать как геометрические векторы в "точеч- ном" трехмерном пространстве или соответственно двумерном пространстве (плоскости). Зафиксировав в трехмерном про-странстве точку, мы можем считать ее стандартным началом каждого вектора, а тогда каждая точка пространства определяется как конец некоторого геометрического вектора.

Эту точку зрения можно обобщить на линейное арифметическое пространство произвольной размерности. Векторы в Rⁿ будем трактовать как точки. Некоторую фиксированную точку О (другими словами, вектор) и ортонормированный базис е в Rⁿ назовем прямоугольной системой координат в Rⁿ, точку О - началом системы координат. Координатами произвольной точки М (это тоже вектор из Rⁿ) в этом пространстве назовем координаты вектора М - О относительно базиса е.

Приведенное обобщение позволяет с единых позиций анализировать геометрию плоскости и трехмерного пространства. Оно также позволяет дать геометрическую интерпретацию некоторым объектам арифметического пространства. Например, множество всех решений однородной системы линейных алгебраических уравнений с геометрической точки зрения представляет собой линейное подпространство арифметического пространства соответствующей размерности. А чем с геометрической точки зрения является множество решений неоднородной системы? Как представить множество решений алгебраического уравнения второй степени, если переменных в этом уравнении четыре или больше?

Определение 9.1. Поверхностью второго порядка в Rⁿ называют множество точек x ∈ Rⁿ, координаты х = (х₁ ... х_n)^T которых в данной прямоугольной системе координат удовлетворяют уравнению

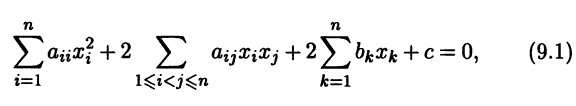
где a_ij, b_k, с - действительные коэффициенты, причем хотя бы один из коэффициентов a_ij, 1 ≤ i ≤ j ≤ n, отличен от нуля.

Замечание 9.1. Поверхность второго порядка в Rⁿ при n = 3 представляет собой обычную поверхность в пространстве, а при n = 2 - кривую на плоскости.

Уравнение (9.1) удобно записывать в матричной форме, полагая a_ij = при i > j и сводя все коэффициенты a_ij в симметрическую матрицу А = (a_ij) порядка n, а слагаемые b_k - в столбец b = (b₁ ... b_n)^T :

х^TАх + 2b^Tх + с = 0. (9.2)

В левой части уравнения (9.2) слагаемые естественным образом распались на три группы. Первая группа представляет собой квадратичную форму х^TАх от координат точки. Ее называют квадратичной формой поверхности (9.1) (кривой при n = 2) второго порядка. Вторая группа представляет собой линейные слагаемые. Ее можно трактовать как координатную запись удвоенного скалярного произведения вектора b со столбцом координат b на вектор х со столбцом координат х. Третья группа в левой части (9.2) представлена одним слагаемым с.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ