Определение квадратичной формы

Определение 8.1. Однородный многочлен второй степени от n переменных с действительными коэффициентами

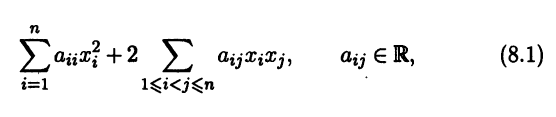
называют квадратичной формой.

Для нас квадратичная форма представляет интерес как способ задания некоторой функции векторного аргумента, определенной в n-мерном линейном пространстве L. Если в этом пространстве выбрать некоторый базис, то квадратичную форму (8.1) можно трактовать как функцию, значение которой определено через координаты х₁, ..., х_n вектора х. Эту функцию часто отождествляют с квадратичной формой.

Квадратичную форму (8.1) можно записать в матричном виде:

х^TАх, (8.2)

где х = (х₁ ... х_n)^T - столбец, составленный из переменных; А = (а_ij) - симметрическая матрица порядка n, называемая матрицей квадратичной формы (8.1).

Ранг матрицы А квадратичной формы называют рангом квадратичной формы. Если матрица А имеет максимальный ранг, равный числу переменных n, то квадратичную форму называют невырожденной, а если RgA < n, то ее называют вырожденной.

Пример 8.1. Квадратичная форма от трех переменных x²₁ + 4x₁x₃ имеет матрицу

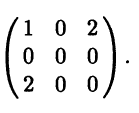
Так как RgA = 2 < 3, то эта квадратичная форма является вырожденной. В матричной записи квадратичная форма имеет вид

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ