Матрицы перехода в евклидовом пространстве

Теорема 7.5. В евклидовом пространстве матрица перехода от одного ортонормированного базиса к другому является ортогональной.

◄ Рассмотрим в произвольном n-мерном евклидовом пространстве Ε два ортонормированных базиса b = (b₁ ... b_n) и е = (e₁ ... е_n). Пусть U - матрица перехода от b к е.

Как следует из определения 1.6, столбцы e₁, ..., е_n матрицы перехода U - это столбцы координат векторов нового базиса е относительно старого базиса b, т.е. U = (е₁ ... е_n), где e_i = be_i, i = 1,n. Поэтому

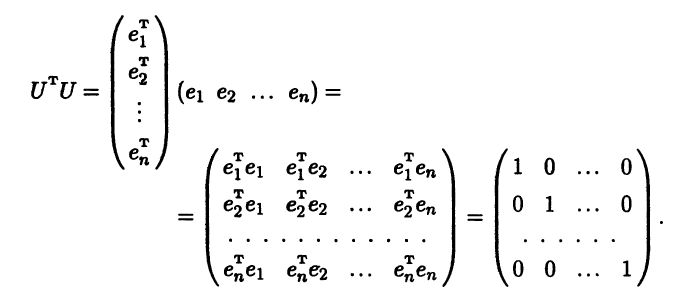
Последнее равенство в приведенной выкладке следует из того, что столбцы e₁,..., е_n - это столбцы координат векторов ортонормированного базиса в ортонормированном базисе, а матричное произведение e_i^Te_j представляет собой запись в координатах скалярного произведения (e_i,e_j), которое в силу ортоиормированности базиса е равно нулю при i ≠ j и единице при i = j.

Мы показали, что U^TU = Е, а это, согласно определению 7.1 ортогональной матрицы, и означает, что U - ортогональная матрица. ►

Теорема 7.6. Пусть b - ортонормированный базис в n-мерном евклидовом пространстве Ε. Любая ортогональная матрица U порядка n является матрицей перехода из базиса b в некоторый другой ортонормированный базис.

◄ Столбцы е₁, ..., е_n матрицы U можно рассматривать как координаты в базисе b некоторых векторов е₁,..., е_n пространства Ε. Матрица U^TU есть не что иное, как матрица Грама для системы векторов е₁, ..., е_n, так как элемент этой матрицы в i-й строке и j-м столбце равен e^T_ie_j, что представляет собой запись в координатах в ортонормированном базисе скалярного произведения (e_i,e_j).

Равенство U^TU = Е означает, что векторы е₁, ..., е_n попарно ортогональны и имеют единичную длину (см. доказательство теоремы 7.5). Поэтому указанная система векторов является линейно независимой (см. теорему 3.4), а так как количество векторов в системе совпадает с размерностью n евклидова пространства, она является базисом (см. теорему 1.4). Этот базис ортонормированный, а матрица U есть матрица перехода из базиса b в базис е. ►

Замечание 7.2. Иногда говорят, что ортогональная матрица состоит из ортонормированных столбцов и строк. Эта терминология мотивируется следующим. Равенства O^TO = Е, OO^T = Е, верные для любой ортогональной матрицы, означают, что системы столбцов и строк матрицы О, рассматриваемых как элементы n-мерного линейного арифметического пространства, являются ортонормированными. #

Напомним, что матрица перехода определяет преобразова-ние координат вектора при замене одного базиса другим. Если х_b - столбец старых координат вектора х, х_e - столбец новых координат, U - матрица перехода из старого базиса в новый, то х_b = Uх_e. Две последние теоремы показывают, что при замене одного ортонормированного базиса другим в соответствующем преобразовании координат х_b = Ux_e матрица U ортогональная.

Замечание 7.3. Любое линейное преобразование линейного пространства представляет собой отображение пространства в себя: каждый вектор линейного пространства меняет свое положение и переходит в свой образ. Преобразование координат не затрагивает элементов пространства, а лишь отражает изменение системы отсчета (базиса). Можно сказать, что преобразование пространства - это изменение окружающего пространства, а преобразование координат - это изменение положения наблюдателя. Эта физическая аналогия показывает, в чем различие между двумя понятиями.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ