Ортогональные операторы

Определение 7.2. Линейный оператор А: Ε → Ε, действующий в евклидовом пространстве Ε, называют ортогональным оператором (или ортогональным преобразованием), если он сохраняет скалярное произведение в Ε, т.е. для любых векторов х, у ∈ Ε выполняется равенство

(Ах,Ау) = (x,y) (7.3)

Так как ортогональный оператор сохраняет скалярное произведение, то он сохраняет норму (длину) вектора и угол между ненулевыми векторами. Действительно,

||Ах||² = (Ах,Ах) = {х,х) = ||х||².

Отсюда, в частности, следует, что если векторы х и у ненулевые, то и векторы Ах и Ау ненулевые. При этом

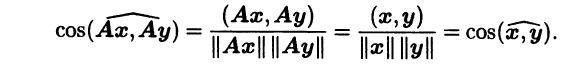
Менее очевидно, что верно и обратное утверждение.

Теорема 7.1. Если линейный оператор А: Ε → Ε в евклидовом пространстве Ε сохраняет евклидову норму: ||Аж|| = ||x||, х ∈ Ε, то этот оператор ортогональный.

◄ Доказательство опирается на следующее тождество:

2(x,y) = ||x + y||² - ||x||² - ||y||²,

верное для любых векторов х и у, в чем можно убедиться, выражая нормы векторов через скалярное произведение. Используя это тождество и сохранение нормы оператором А, получаем

(Ах,Ау) = ||A(x + у)||² - ||Аx||² - ||Ау||² = ||x + у||² - ||x||² - ||y||² = (x,y),

где х и у - произвольные векторы пространства Ε. ►

Теорема 7.1 позволяет привести примеры ортогональных операторов. В пространствах V₂ и V₃ свободных векторов ортогональными являются линейные операторы, сохраняющие расстояние. Например, линейный оператор поворота вектора на фиксированный угол (см. пример 4.2) является ортогональным, так как при таком повороте длины векторов не изменяются. Линейный оператор симметрии относительно прямой на плоскости или относительно плоскости в пространстве также является ортогональным.

Теорема 7.2. Пусть А: Ε → Ε - ортогональный оператор в евклидовом пространстве Ε и е = (e₁ ... е_n) - произвольный ортонормированный базис в Ε. Тогда система векторов Ае = (Ae₁ ... Ае_n) является ортонормированным базисом в Ε.

◄ Достаточно подсчитать все парные скалярные произведения векторов Ае_i. В силу ортогональности оператора А имеем

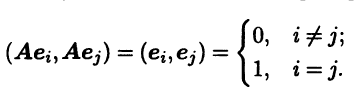
Видим, что различные векторы Ае_i и Ae_j ортогональны, а норма каждого из них равна единице. Поэтому система векторов Ае = (Ае₁ ... Ае_n) состоит из ненулевых векторов и ортогональна. Согласно теореме 3.4, она линейно независима. Количество векторов в линейно независимой системе Ае равно dimΕ = n, поэтому, согласно теореме 1.4, это базис, притом ортонормированный. ►

Теорема 7.3. Если линейный оператор А: Ε → Ε в евклидовом пространстве Ε переводит какой-либо ортонормированный базис е = (e₁ ... е_n) в ортонормированный базис Ае = (Ae₁ ... Ае_n), то этот оператор ортогональный.

◄ Если вектор х имеет столбец координат х = (х₁ ... х_n)^T в базисе е, то его образ Ах имеет тот же столбец координат в базисе Ае, так как, согласно определению линейного оператора,

Ах = А(х₁е₁ +... + x_ne_n) = x₁(Ae₁) + ... + x_n(Ae_n).

Выберем два произвольных вектора х = x₁e₁ + ... + x_ne_n и y = y₁e₁ + ... + y_nе_n. Их скалярное произведение в ортонормированием базисе е выражается формулой

(х,у) = x₁y₁ + ... + x_ny_n,

но той же формулой выражается и скалярное произведение (Ах,Ау), если в качестве базиса взять Ае. Поэтому соотношение (Ах,Ау) = (х,у) выполняется для любых векторов x и у, что, согласно определению 7.2, означает ортогональность оператора А. ►

Теорема 7.4. Если матрица линейного оператора в некотором ортонормированием базисе ортогональна, то этот оператор является ортогональным. Наоборот, матрица ортогонального оператора в любом ортонормированием базисе является ортогональной.

◄ Выберем в евклидовом пространстве Ε любой ортонормированный базис е. Тогда для любых векторов x и у, имеющих в этом ортонормированном базисе е столбцы координат х и у соответственно, выполнено равенство (х,у) = х^Tу (это запись скалярного произведения в ортонормированном базисе, см. 3.7).

Пусть матрица А линейного оператора А в ортонормированном базисе является ортогональной. Тогда выполняется соотношение А^TА = Е и, следовательно, равенство

х^T(А^TА)у = х^TЕу (7.4)

верно для любых столбцов х и у. Но это равенство представляет собой матричную запись равенства скалярных произведений (Ах,Ау) = (х,у) для векторов х и у, имеющих столбцы координат х и у в этом же ортонормированном базисе. Мы приходим к заключению, что оператор ортогональный.

Докажем обратное утверждение теоремы. В любом ортонормированном базисе соотношение (7.3) в координатах имеет вид

(Ах)^T(Ау) = х^Tу,

т.е. его можно записать в виде (7.4). Как мы ранее доказали (см. лемму на с. 185), из этого равенства, выполняющегося для любых столбцов хну, следует равенство матриц А^TА = Е, что и означает ортогональность матрицы А. ►

Замечание 7.1. Напомним, что матрица линейного оператора состоит из столбцов координат образов базисных векторов. Имея это в виду, нетрудно заметить, что равенство А^TА = Е означает, что столбцы матрицы А, как элементы n-мерного линейного арифметического пространства со стандартным скалярным произведением, попарно ортогональны и имеют единичную длину. Действительно, в i-й строке и j-м столбце матрицы А^TА стоит скалярное произведение i-ro и j-го столбцов матрицы А. Это позволяет свести теорему 7.4 к теореме 7.3.

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ