Ортогональные матрицы и их свойства

Определение 7.1. Квадратную матрицу О называют ортогональной, если она удовлетворяет условию

О^TО = Е, (7.1)

где Е - единичная матрица.

Пример 7.1. Простейшей ортогональной матрицей является единичная матрица Е, так как Е^TЕ = ЕЕ = Е. Напротив, нулевая матрица не является ортогональной: Θ^TΘ = Θ ≠ Е.

Пример 7.2. Матрица

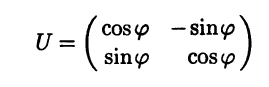
является ортогональной, поскольку U^TU = Е. Это можно про-верить непосредственно. #

Из определения 7.1 вытекает ряд свойств ортогональных матриц.

Свойство 7.1. Определитель ортогональной матрицы О может иметь одно из двух возможных значений: det О = ±1.

◄ Согласно равенству (7.1), имеем det(О^TО) = detЕ. Вспомнив [III], что определитель произведения матриц равен произведению их определителей, а при транспонировании матрицы определитель не меняется, получим

det(O^TO) = detО^TdetО = (detО)².

Так как detE = 1, то и (detO)p = 1. Следовательно, detO = ±1. ►

Свойство 7.2. Матрица, обратная к ортогональной матрице О, совпадает с ее транспонированной матрицей, т.е. O^-1 = О^T.

◄ Согласно свойству 7.1, ортогональная матрица невырождена и потому имеет обратную матрицу О^-1. Умножая равенство (7.1) справа на матрицу О^-1, получаем

(O^TO)O^-1-1) = О^-1. Но OO^-1 = Е, поэтому О^T = О^-1. ►

Свойство 7.3.

Произведение ортогональной матрицы О на транспонированную к ней равно единичной матрице, т.е. ОО^T = Е.

◄ Согласно свойству 7.2 и определению обратной матрицы, ОО^T = OO^-1 = Е. ►

Свойство 7.4. Матрица, транспонированная к ортогональной матрице, тоже является ортогональной.

◄ Нужно для произвольной ортогональной матрицы О доказать равенство

(О^T)^TО^T = Е, (7.2)

представляющее собой запись соотношения (7.1) для матрицы О^T. Так как, согласно свойству операции транспонирования, (О^T)^T = О, равенство (7.2) эквивалентно равенству ОО^T = Е, которое верно в силу свойства 7.3. ►

Свойство 7.5. Произведение двух ортогональных матриц О и Q одного порядка является ортогональной матрицей.

◄ Для доказательства достаточно проверить выполнение равенства (7.1) для матрицы OQ:

(OQ)^T(OQ) = (Q^TO^T)OQ = Q^T(O^TO)Q = Q^TEQ = Q^TQ = E.

В этих выкладках Е, как обычно, обозначает единичную матрицу. ►

Свойство 7.6. Матрица, обратная к ортогональной матрице, тоже является ортогональной.

◄ Согласно свойству 7.1, ортогональная матрица невырождена, а потому имеет обратную. Согласно свойству 7.2, матрица, обратная к ортогональной, совпадает с транспонированной. Наконец, согласно свойству 7.4, матрица, транспонированная к ортогональной, является ортогональной. ►

Пример 7.3. Рассмотрим матрицу U из примера 7.2. Так как она ортогональна, то обратную матрицу легко найти, используя свойство 7.6:

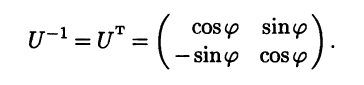
1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ