Смешанное произведение трех векторов
Решение задачТройкой векторов называются три вектора, если указано, какой из них считйется первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись а, b, с означает, что вектор а считается первым, b - вторым, с - третьим.
Тройка некомпланарных векторов а, b, с называется правой, если составляющие ее Векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как располо- жены большой, указательный и средний пальцы правой руки. Если векторы а,b, с расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.
Смешанным произведением трех векторов а, b, c называется число, равное векторному произведению [ab], умноженному ска- лярно на вектор с, т. е. [ab]с.
Имеет место тождество: [ab] с = а [bс], ввиду чего для обозначения смешанного произведения [аb] с употребляется более простой символ: аbс. Таким образом,
аЬс=[аb]с, аЬс = а[bс].
Смешанное произведение аbс равно объему параллелепипеда, построенного на векторах а, b, с, взятому со знаком плюс, если тройка аbс правая, со знаком минус, если эта тройка левая. Если векторы а, b, с компланарны (и только в этом случае), смешанное произведение аbс равно нулю; иначе говоря, равенство
аbс = О
есть необходимое и достаточное условие компланарности векторов а, b, с.
Если векторы а, b, с заданы своими координатами:
a = {X1;Y1;Z1}, b = {X2;Y2;Z2} с = {X32;Y3;Z3}
то смешанное произведение аbс определяется формулой
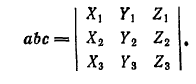
Напомним, что система координатных осей предполагается правой (вместе с тем является правой и тройка векторов i , j ,k).
865. Определить, какой является тройка a, b, с (правой или левой), если
1) а = k, b = i, с = j; 2) a = i, b = k, с = j;
3) a = j, b = i, с = k; 4) a = i + j, b = j, с = k;
5) а = i + j, b = i - j, с = j;
6) a = i + j, b = i - j, с = k.
866. Векторы а, b, с, образующие правую тройку, взаимно перпендикулярны. Зная, что |a| = 4, |b| = 2, |с| = 3, вычислить abc.
867. Вектор с перпендикулярен к векторам a и b, угол между a и b равен 30°. Зная, что |a| = 6, |b| = 3, |с| = 3, вычислить abc.
868. Доказать, что |abc| ≤ |а||b||с|; в каком случае здесь может иметь место знак равенства?
869. Доказать тождество (a + b)(b + с) (с + a) = 2abc.
870. Доказать тождество ab (с + λa + μb) = abc, где λ и μ - какие угодно числа.
871. Доказать, что векторы а, b, с, удовлетворяющие условию [ab] + [bс] + [са] = 0, компланарны.
872. Доказать, что необходимым и достаточным условием компланарности векторов a, b, с является зависимость αа + βb + γс = 0, где по крайней мере одно из чисел а, р, у не равно нулю.
873. Даны три вектора: а = { 1; -1; 3}, b = {- 2; 2; 1}, с = {3; -2; 5}. Вычислить abc.
874. Установить, компланарны ли векторы a, b, с, если:
1) a = {2; 3; -1}, b = {1; -1; 3}, с = {1;9;-11};
2) a = {3; -2; 1}, b = {2; 1; 2}, с = {3; -1; -2};
3) а = {2; -1; 2}, b = {1; 2; -3}, с = {3; -4; 7}.
875. Доказать, что четыре точки A(1; 2; -1), B(0; 1; 5), С(-1; 2; 1), D(2; 1; 3) лежат в одной плоскости.
877. Даны вершины тетраэдра: А(2; 3; 1), В(4; 1; -2), С (6; 3; 7), D (-5; -4; 8). Найти длину его высоты, опущенной из вершины D.
878. Объем тетраэдра v - 5, три его вершйны находятся в точках А (2; 1; -1), 5(3; 0; 1), С (2; - 1; 3). Найти координаты четвертой вершины D, если известно, что она лежит на оси Оу.