Скалярное произведение векторов
Решение задачСкалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение векторов а, b обозначается символом ab (порядок записи сомножителей безразличен, т. е. ab = ba).
Если угол между векторами а, Ь обозначить через φ , то их скалярное произведение можно выразить формулой
аb = |а| • |b| • cosφ (1)
Скалярное произведение векторов а, b можно выразить также формулой
аb = |а| • прab, или аb = |b| • прa.
Из формулы (1) следует, что аb > 0, если φ - острый угол, аb < 0, если угол φ - тупой; аb = 0 в том и только в том случае, когда векторы а и b перпендикулярны (в частности, аb = 0, если а = 0 или Ь = 0).
Скалярное произведение аа называется скалярным квадратом вектора и обозначается символом а2. Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
а2 = |а|2
Если векторы а и b заданы своими координатами:
а = {X1; Y1; Z1}, b = {Х2; У2; Z2]
то их скалярное произведение может быть вычислено по формуле
ab = X1X2 + Y1Y2 + Z1Z2
Отсюда следует необходимое и достаточное условие перпендикулярности векторов:
X1X2 + Y1Y2 + Z1Z2 = 0
Угол φ между векторами
а = {X1; Y1; Z1} и b = [Х2; У2; Z2}
дается формулой cosφ = ab/ (|a| • |b|), или в координатах
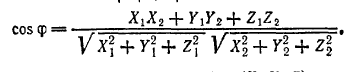
Проекция произвольного вектора S = {X;Y; Z) на какую-нибудь ось и определяется формулой
прu S = Se,
где е - единичный вектор, направленный по оси u. Если даны углы α, β, γ которые ось u составляет с координатными осями, то е = {cosα; cosβ; cosγ } и для вычисления проекции вектора S может служить формула
прuS = X cosα + Y cosβ + Z cosγ
795. Векторы а и b образуют угол φ = 2/3π; зная, что |а| = 3, |b| = 4, вычислить: 1) ab; 2) а2; 3) b2; 4) (а+b)2; 5) (За - 2b) (а + 2b); 6) (а - b)2; 7) (За + 2b)2.
796. Векторы а и b взаимно перпендикулярны; вектор с образует с ними углы, равные π/3; зная, что |а|= 3, |b| = 5, |с| = 8, вычислить: 1) (За - 2b)(b + Зс); 2) (а + b + с)2; 3) (а + 2b - Зс)2.
797. Доказать справедливость тождества (а + b)2 + (а - b)2 = 2 (а2 + b2) и выяснить его геометрический смысл.
798. Доказать, что - ab &le ab ≤ ab; в каких случаях здесь может иметь место знак равенства?
799. Считая, что каждый из векторов а, b, с отличен от нуля, установить, при каком их взаимном расположении справедливо равенство: (ab)с = a(bc).
800. Даны единичные векторы a, b и с, удовлетворяющие условию a + b + с = 0. Вычислить ab + bc + ca.
801. Даны три вектора a, b и с, удовлетворяющие условию а + b + с = 0. Зная, что |a| = 3, |b| = 1 и |с| = 4, вычислить ab + bc + са.
802. Векторы a, b, с попарно образуют друг с другом углы, каждый из которых равен 60°. Зная, что |а| = 4, |b| = 2 и |с| = 6, определить модуль вектора р = a + b + с.
803. Дано, что |а| = 3, |b| = 5. Определить, при каком значении α векторы a + αb, a - αb будут взаимно перпендикулярны.
804. Какому условию должны удовлетворять векторы а и b, чтобы вектор a + b был перпендикулярен к вектору a - b.
805. Доказать, что вектор р = b(ас) - с(аb) перпендикулярен к вектору а.
806. Доказать, что вектор р = b - a(ab)/a2 перпендикулярен к вектору а.
807. Даны векторы AB = b и AC = с, совпадающие со сторонами треугольника ABC. Найти разложение по базису b, с вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD.
808. Векторы а и b образуют угол φ = π/6 зная, что |a| = √3, |b| = 1, вычислить угол α между векторами р = а + b и q = a - b.
809. Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.
810. Определить геометрическое место концов переменного вектора х, если его начало находится в данной точке А и вектор х удовлетворяет условию ха = α, где а -данный вектор и α - данное число.
811. Определить геометрическое место концов пере-менного вектора х, если его начало находится в данной точке А и вектор х удовлетворяет условиям ха = α, xb = β, где а, b - данные неколлинеарные векторы и α, β - данные числа.
812. Даны векторы а ={4; -2; -4}, b = {6; -3; 2}. Вычислить: 1) ab; 2) √а2; 3) √b2; 4) (2а - 3b) (а + 2b); 5) (а + b)2 ; 6) (а - b)2 .
813. Вычислить, какую работу производит сила f = {3; -5; 2}, когда ее точка приложения перемещается из начала в конец вектора s(2; -5; -7) *).
814. Даны точки A(-1; 3; -7), В (2; -1; 5) и С(0, 1; -5). Вычислить: 1) (2AB - CB) (2BC + BA); 2) √(AB2); з) √(AC2); 4) найти координаты векторов (ABAC) BC и AB(ACBC).
815. Вычислить, какую работу производит сила f= {3; -2, -5}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения А(2; -3; 5) в положение В{3; -2; -1).
816. Даны три силы М = {3; -4; 2}, N = {2; 3; -5} и р = {-3; -2; 4}, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения M1 (5; 3; -7) в положение М2(4; -1; -4).
817. Даны вершины четырехугольника A(1; -2; 2), В( 1; 4; 0), С(-4; 1; 1) и D{-5; -5; 3). Доказать, что его диагонали АС и BD взаимно перпендикулярны.
818. Определить, при каком значении α векторы а = αi - 3j + 2k и b = i + 2j - ak взаимно перпендикулярны.
819. Вычислить косинус угла, образованного векторами а = {2; -4; 4} и b = (-3; 2; 6}.
820. Даны вершины треугольника A(-1; -2; 4), В(-4; -2; 0) и С(3; -2; 1). Определить его внутренний угол при вершине В.
821. Даны вершины треугольника A(3; 2; - 3), B(5; 1; -1) и С(1; -2; 1). Определить - его внешний угол при вершине А.
822. Вычислив внутренние углы треугольника A(1; 2; 1), В(3; -1; 7), С(7; 4; -2), убедиться, что этот треугольник равнобедренный.
823. Вектор х, коллинеарный вектору а = {6; -8; -7,5}, образует острый угол с осью Oz. Зная, что |x| = 50, найти его координаты.
824. Найти вектор х, коллинеарный вектору а = {2; 1; -1} и удовлетворяющий условию ха = 3.
825. Вектор х, перпендикулярный к векторам а = 3i + 2j + 2k и b = 18i - 22j - 5k, образует с осью Оу тупой угол. Найти его координаты, зная, что |x| = 14.
826. Найти вектор зная, что он перпендикулярен к векторам а = {2; 3; -1} и b = {1; -2; 3} и удовлетворяет условию х (2i - j + k) = - 6.
827. Даны два вектора: а = {3; - 1; 5} и b = {1; 2; -3}. Найти вектор х «при условии, что он перпендикулярен к оси Oz и удовлетворяет условиям: ха = 9, хb = - 4,
828. Даны три вектора: а = 2i - j + k, b = i - 3j + 2k и с = 3i + 2j - 4k. Найти вектор x, удовлетворяющий условиям: ха = - 5, хb = - 11, хс = 20.
829. Найти проекцию вектора S = {4; -3; 2} на ось, составляющую с координатными осями равные острые углы.
830. Найти проекцию вектора S={√2; -3; -5} на ось, составляющую с координатными осями Ox, Oz углы α = 45°, γ = 60°, а с осью Оу - острый угол β
831. Даны две точки A (3; -4; -2), В (2; 5; -2). Найти проекцию вектора АВ на ось, составляющую с координатными осями Ох, Оу углы α = 60°, β = 120°, а с осью Oz - тупой угол γ.
832. Вычислить проекцию вектора а = {5; 2; 5} на ось вектора b = {2; -1; 2}.
833. Даны три вектора: a = 3i - 6j - k, b = i + 4j - 5k и с = 3i - 4j - 12k. Вычислить прc(а + b).
834. Даны три вектора: а = { 1; -3; 4), b = {3; -4; 2} и c = {- 1; 1; 4}. Вычислить прb + ca.
835. Даны три вектора: а = - 2i + j + k, b = i + 5j и с = 4i + 4j - 2k. Вычислить прc(3а - 2b),
836. Сила, определяемая вектором R = {1; -8; -7}, разложена по трем направлениям, одно из которых задано вектором а = 2i + 2j+ k. Найти составляющую силы R в направлении вектора а.
837. Даны две точки М(-5; 7; -6) и N(7; -9; 9). Вычислить проекцию вектора а = { 1; -3; 1} на ось вектора MN
838. Даны точки А(-2; 3; -4), В(3; 2; 5), С(1; -1; 2), D (3; 2; -4), Вычислить прCDAB.