Специальные виды уравнения плоскости

Векторное и параметрические уравнения плоскости. Пусть r₀ и r — радиус-векторы точек М₀ и M соответственно. Тогда M₀M = r — r₀, и условие (5.1) принадлежности точки M плоскости, проходящей через точку М₀ перпендикулярно ненулевому вектору n (рис. 5.2, а), можно записать с помощью скалярного произведения в виде соотношения

n(r - r₀) = 0, (5.4)

которое называют векторным уравнением плоскости.

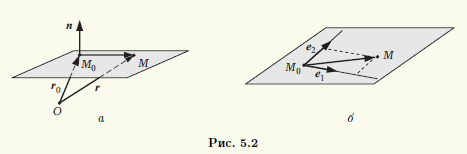
Фиксированной плоскости в пространстве соответствует множество параллельных ей векторов, т.е. пространство V₂. Выберем в этом пространстве базис e₁, e₂, т.е. пару неколлинеарных векторов, параллельных рассматриваемой плоскости, и точку M₀ на плоскости. Если точка M принадлежит плоскости, то это эквивалентно тому, что ей параллелен вектор M₀M (рис. 5.2, б), т.е. он принадлежит указанному пространству V₂. Это означает, что существует разложение вектора M₀M в базисе e₁, e₂, т.е. существуют такие числа t₁ и t₂, для которых M₀M = t₁e₁ + t₂e₂. Записав левую часть этого уравнения через радиус-векторы r₀ и r точек М₀ и M соответственно, получаем векторное параметрическое уравнение плоскости

r = r₀ + t₁e₁ + t₂e₂, t₁ , t₁ ∈ R. (5.5)

Чтобы перейти от равенства векторов в (5.5) к равенству их координат, обозначим через (x₀; y₀; z₀), (x; y; z) координаты точек M₀, M и через {e_1x; e_1y; e_1z}, {e_2x; e_2y; e_2z} координаты векторов e₁, e₂. Приравнивая одноименные координаты векторов r и r₀ + t₁e₁ + t₂e₂, получаем параметрические уравнения плоскости

Плоскость, проходящая через три точки. Предположим, что три точки M₁, M₂ и М₃ не лежат на одной прямой. Тогда существует единственная плоскость π, которой эти точки принадлежат. Найдем уравнение этой плоскости, сформулировав критерий принадлежности произвольной точки M данной плоскости π. Затем запишем этот критерий через координаты точек. Указанным критерием является описание плоскости π как множества тех точек M, для которых векторы M₁M₂, M₁M₃ и M₁M компланарны. Критерием компланарности трех векторов является равенство нулю их смешанного произведения (см. 3.2). Смешанное произведение вычисляется с помощью определителя третьего порядка, строками которого являются координаты векторов в ортонормированном базисе. Поэтому, если (x_i; yx_i; Zx_i) — координаты точек Mx_i, i = 1, 2, 3, а (x; y; z) — координаты точки M, то M₁M = {х—x₁; у—y₁; z—z₁}, M₁M₂ = {x₂—x₁; y₂—y₁; z₂—z₁}, M₁M₃ = {x₃—x₁; y₃—y₁; z₃—z₁} и условие равенства нулю смешанного произведения этих векторов имеет вид

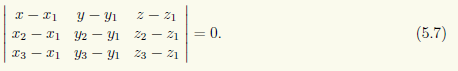
Вычислив определитель, получим линейное относительно x, y, z уравнение, являющееся общим уравнением искомой плоскости. Например, если разложить определитель по 1-й строке, то получим

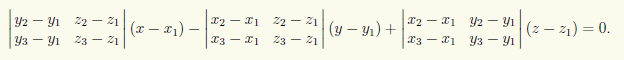
Это равенство после вычисления определителей и раскрытия скобок преобразуется к общему уравнению плоскости.

Отметим, что коэффициенты при переменных в последнем уравнении совпадают с координатами векторного произведения M₁M₂ × M₁M₃. Это векторное произведение, будучи произведением двух неколлинеарных векторов, параллельных плоскости π, дает ненулевой вектор, перпендикулярный π, т.е. ее нормальный вектор. Так что появление координат векторного произведения в качестве коэффициентов общего уравнения плоскости вполне закономерно.

Рассмотрим следующий частный случай плоскости, проходящей через три точки. Точки M₁ (a; 0; 0), M₂(0; b; 0), M₃(0; 0; c), abc ≠ 0, не лежат на одной прямой и задают плоскость, которая отсекает на осях координат отрезки ненулевой длины (рис. 5.3). Здесь под " длинами отрезков " понимают значение ненулевых координат радиус-векторов точек M_i, i = 1,2,3.

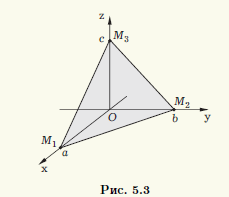
Поскольку M₁M₂ = {—a; b;0}, M₁M₃ = {—a; 0; c}, M₁M = (x—a; y; z), то уравнение (5.7) принимает вид

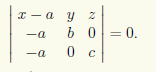
Вычислив определитель, найдем bc(x — a) + acy + abz = 0, разделим полученное уравнение на abc и перенесем свободный член в правую часть,

x/a + y/b + z/c = 1.

Это уравнение называют уравнением плоскости в отрезках.

Пример 5.2. Найдем общее уравнение плоскости, которая проходит через точку с координатами (1; 1; 2) и отсекает от осей координат отрезки одинаковой длины.

Уравнение плоскости в отрезках при условии, что она отсекает от осей координат отрезки равной длины, скажем a ≠ 0, имеет вид x/a + y/b + z/c = 1. Этому уравнению должны удовлетворять координаты (1; 1; 2) известной точки на плоскости, т.е. выполняется равенство 4/a = 1. Поэтому a = 4 и искомым уравнением является x + y + z — 4 = 0.

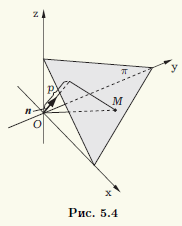
Нормальное уравнение плоскости. Рассмотрим некоторую плоскость π в пространстве. Фиксируем для нее единичный нормальный вектор n, направленный из начала координат "в сторону плоскости ", и обозначим через р расстояние от начала O системы координат до плоскости π (рис. 5.4). Если плоскость проходит через начало системы координат, то p = 0, а в качестве направления для нормального вектора n можно выбрать любое из двух возможных.

Если точка M принадлежит плоскости π, то это эквивалентно тому, что ортогональная проекция вектора OM на направление вектора n равна р, т.е. выполнено условие nOM = пр_nOM = р, так как длина вектора n равна единице.

Обозначим координаты точки M через (x; y; z) и пусть n = {cosα; cosβ; cosγ} (напомним, что для единичного вектора n его направляющие косинусы cosα, cosβ, cosγ одновременно являются и его координатами). Записывая скалярное произведение в равенстве nOM = р в координатной форме, получаем нормальное уравнение плоскости

xcosα + ycosbeta; + zcosγ — p = 0.

Аналогично случаю прямой на плоскости, общее уравнение плоскости в пространстве можно преобразовать в ее нормальное уравнение делением на нормирующий множитель.

Для уравнения плоскости Ax + By + Cz + D = 0 нормирующим множителем является число ±√(A² + B² + C²), знак которого выбирается противоположным знаку D. По абсолютной величине нормирующий множитель представляет собой длину нормального вектора {A; B; C} плоскости, а знак соответствует нужному направлению единичного нормального вектора плоскости. Если плоскость проходит через начало системы координат, т.е. D = 0, то знак нормирующего множителя можно выбрать любым.