Алгебраические поверхности первого порядка

Уравнение первого порядка с тремя неизвестными имеет вид Ax + Ву + Cz + D = 0, причем хотя бы один из коэффициентов A, В, C должен быть отличен от нуля. Оно задает в пространстве в прямоугольной системе координат Oxyz алгебраическую поверхность первого порядка.

Свойства алгебраической поверхности первого порядка во многом аналогичны свойствам прямой на плоскости — геометрическому образу уравнения первого порядка с двумя неизвестными.

Теорема 5.1. Любая плоскость в пространстве является поверхностью первого порядка и любая поверхность первого порядка в пространстве есть плоскость.

◄ Как утверждение теоремы, так и ее доказательство аналогичны теореме 4.1. Действительно, пусть плоскость π задана своей точкой М₀ и ненулевым вектором n, который ей перпендикулярен. Тогда множество всех точек в пространстве разбивается на три подмножества. Первое состоит из точек, принадлежащих плоскости, а два других — из точек, расположенных по одну и по другую стороны плоскости. Какому из этих множеств принадлежит произвольная точка M пространства, зависит от знака скалярного произведения nM₀M. Если точка M принадлежит плоскости (рис. 5.1, а), то угол между векторами n и M₀M прямой, и поэтому, согласно теореме 2.7, их скалярное произведение равно нулю:

nM₀M = 0

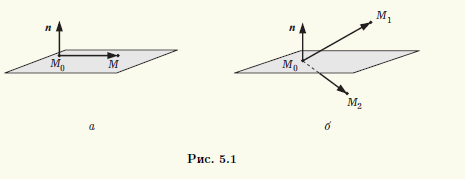
Если же точка M не принадлежит плоскости, то угол между векторами n и M₀M острый или тупой, и поэтому nM₀M > 0 или nM₀M < 0 соответственно (см. доказательство теоремы 2.7), причем знак этого скалярного произведения один и тот же для всех точек, расположенных по одну сторону от плоскости (рис. 5.1, б).

Обозначим координаты точек M₀, M и вектора n через (х₀; у₀; z₀), (х; у; z) и {A; В; C} соответственно. Так как M₀M = {х — х₀0; у — у₀; z — z₀}, то, записывая скалярное произведение из (5.1) в координатной форме (2.14) как сумму попарных произведений одноименных координат векторов n и M₀M, получаем условие принадлежности точки M рассматриваемой плоскости в виде

A(x — х₀) + В(у — у₀) + C (z — z₀) = 0. (5.2)

Раскрытие скобок дает уравнение

Ax + Ву + Cz + D = 0, (5.3)

где D = — Ax₀ — Ву₀ — Cz₀ и хотя бы один из коэффициентов A, В, или C отличен от нуля, так как вектор n = {A; В; C} ненулевой. Это означает, что плоскость является геометрическим образом уравнения (5.3), т.е. алгебраической поверхностью первого порядка.

Проведя изложенное доказательство первого утверждения теоремы в обратном порядке, мы докажем, что геометрическим образом уравнения Ax + Ву + Cz + D = 0, A² + В² + C² = 0, является плоскость. Выберем три числа (х = х₀, у = у₀, z = z₀), удовлетворяющих этому уравнению. Такие числа существуют. Например, при A ≠ 0 можно положить у₀ = 0, z₀ = 0 и тогда х₀ = — D/A. Выбранным числам соответствует точка M₀(x₀; у₀; z₀), принадлежащая геометрическому образу заданного уравнения. Из равенства Ax₀ + Ву₀ + Cz₀ + D = 0 следует, что D = — Ax₀ — Ву₀ — Cz₀. Подставляя это выражение в рассматриваемое уравнение, получаем Ax + Ву + Cz — Ax₀ — Ву₀ — Cz₀ = 0, что равносильно (5.2). Равенство (5.2) можно рассматривать как критерий ортогональности векторов n = {A; В; C} и M₀M, где точка M имеет координаты (х; у; z). Этот критерий выполнен для точек плоскости, проходящей через точку M₀ перпендикулярно вектору n = {A; В; C}, и не выполнен для остальных точек пространства. Значит, уравнение (5.2) есть уравнение указанной плоскости. ►

Уравнение Ax + Ву + Cz + D = 0 называют общим уравнением плоскости. Коэффициенты A, В, C при неизвестных в этом уравнении имеют наглядный геометрический смысл: вектор n = {A; В; C} перпендикулярен плоскости. Его называют нормальным вектором плоскости. Он, как и общее уравнение плоскости, определяется с точностью до (ненулевого) числового множителя.

По известным координатам точки, принадлежащей некоторой плоскости, и ненулевого вектора, перпендикулярного ей, с помощью (5.2) уравнение плоскости записывается без каких-либо вычислений.

Пример 5.1. Найдем общее уравнение плоскости, перпендикулярной радиус-вектору точки A(2; 5; 7) и проходящей через точку М₀(3; — 4; 1).

Поскольку ненулевой вектор OA = {2; 5; 7} перпендикулярен искомой плоскости, то ее уравнение типа (5.2) имеет вид 2(х — 3) + 5(у + 4) + 7(z— 1) = 0. Раскрывая скобки, получаем искомое общее уравнение плоскости 2х + 5у + 7z + 7 = 0.