Вычисление обратной матрицы

Применяют два основных метода вычисления обратной матрицы. Первый вытекает из теоремы 11.2 и состоит в следующем. Пусть дана квадратная матрица A порядка n. Матрицу A*, транспонированную к матрице (A_ij) алгебраических дополнений, называют присоединенной. Как следует из доказательства теоремы 11.2, если A — невырожденная матрица, то обратная к ней имеет вид A^-1 = 1/detA A*.

Таким образом, чтобы для квадратной матрицы порядка n найти обратную матрицу, надо вычислить один определитель порядка n и составить присоединенную матрицу, т.е. вычислить n² определителей порядка n — 1. Метод присоединенной матрицы эффективен при n = 2 или n = 3, но при росте n становится слишком трудоемким.

Пример 11.1. Выясним, имеет ли матрица 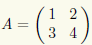обратную и если имеет найдем ее.

Поскольку det A = -2, матрица A является невырожденной и, согласно теореме 11.2, имеет обратную. Для ее вычисления последовательно находим

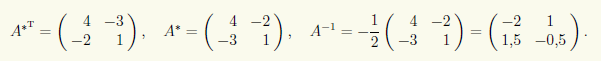
Отметим, что для квадратной матрицы A второго порядка присоединенная матрица A* получается перестановкой в A диагональных элементов и изменением знака двух других.

Проверка ответа выполняется в соответствии с определением 11.1 обратной матрицы:

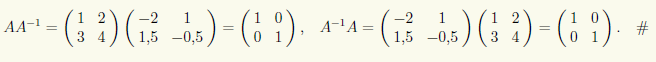
Второй метод вычисления обратной матрицы состоит в преобразовании исходной матрицы к более простому виду с помощью элементарных преобразований строк. Чтобы найти матрицу A^-1, обратную к A, фактически надо решить матричное уравнение AX = E. Отметим, что если над матрицей A выполняется какое-либо элементарное преобразование строк, то это же преобразование осуществляется и над матрицей AX, поскольку любое элементарное преобразование строк матрицы эквивалентно умножению ее слева на соответствующую матрицу специального вида (см. 10.5). Таким образом, если в уравнении AX = E над матрицами A и E одновременно выполнить какое-либо элементарное преобразование строк, т.е. домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное уравнение A₁X = B₁. Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное преобразование строк имеет обратное элементарное преобразование строк. Последовательность элементарных преобразований строк надо подобрать так, чтобы на s-м шаге матрица А превратилась в единичную матрицу. В результате этих s шагов получается уравнение A_sX = B_s, где A_s = E, т.е. X = B_s. Итак, поскольку A-1 является решением уравнения AX = E, которое эквивалентно X = B_s, то A^-1 = B_s.

Чтобы синхронно выполнять преобразования над матрицами в левой и правой частях матричного уравнения AX = E, записывают блочную матрицу (A | E) и выполняют такие элементарные преобразования строк этой матрицы, чтобы вместо A получить единичную матрицу E.

Пример 11.2. Продемонстрируем изложенный метод нахождения обратной матрицы для матрицы из примера 11.1. Для этого записываем матрицу (A|E) и выполняем элементарные преобразования ее строк в следующем порядке: