Обратная матрица и ее свойства

Определение 11.1. Пусть А — квадратная матрица порядка n. Квадратную матрицу B того же порядка называют обратной к А, если AB = BA = E, где E — единичная матрица порядка n.

Обратную матрицу обозначают A^-1. Она позволяет определить целую отрицательную степень матрицы А. А именно, для n > 0 полагают A^-n = (A^-1)ⁿ.

Теорема 11.1. Если квадратная матрица А имеет обратную матрицу, то обратная матрица единственная.

◄ Предположим, что матрица А имеет две обратные матрицы В и В'. Тогда, согласно определению 11.1 обратной матрицы, выполнены, в частности, равенства AB' = E и BA = E. Используя ассоциативность умножения матриц, получаем B = BE = В(AB') = (BA)B' = EB' = B', т.е. матрицы B и B' совпадают. ►

Квадратная матрица не всегда имеет обратную. Установить, имеет ли данная матрица обратную, позволяет следующий критерий.

Теорема 11.2. Для того чтобы квадратная матрица А порядка n имела обратную, необходимо и достаточно, чтобы detА ≠ 0.

◄ Необходимость. Пусть A^-1 — матрица, обратная к А. Тогда det(AA^-1) = detE = 1, но, согласно свойству определителей, det(AA^-1) = detA detA^-1. Поэтому detA detA^-1 = 1 и, следовательно, detА ≠ 0.

Достаточность. Пусть detА ≠ 0. Обозначим через A_ij алгебраическое дополнение матрицы А, соответствующее элементу a_ij , т.е. A_ij = (—1)^i+jM_ij, где M_ij — минор этого же элемента.

Раскрывая определитель матрицы А по i-й строке, получаем равенства

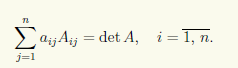
По свойствам определителей, для любых индексов k ≠ i выполнено равенство

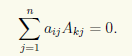
Рассмотрим теперь квадратную матрицу В порядка n с элементами b_ij = A_ji/detA . Матрица C = AB имеет элементы

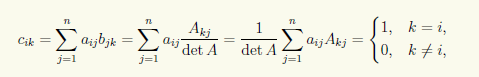
т.е. C — единичная матрица.

Аналогично матрица C' = BA имеет элементы

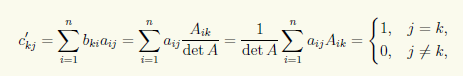
следовательно, матрица C' также является единичной.

Согласно определению 11.1, матрица B является обратной для A: B = A^-1. ►

Следствие 11.1. Если квадратная матрица A имеет обратную, то detA^-1 = (detA)^-1.

◄ Действительно, detA^-1 detA = det(A^-1A) = detE = 1. ►

Квадратную матрицу с ненулевым определителем называют невырожденной или неособой. В противном случае, когда определитель матрицы равен нулю, ее называют вырожденной. Итак, для существования обратной матрицы A^-1 необходимо и достаточно, чтобы матрица A была невырожденной.

Теорема 11.3. Если квадратные матрицы A и B порядка n имеют обратные матрицы, то и их произведение имеет обратную матрицу, причем (AB)^-1 = B^-1A^-1.

◄ В соответствии с определением 11.1 обратной матрицы достаточно доказать два равенства: (AB)B^-1A^-1 = E, (B^-1A^-1)(AB) = E. Используя ассоциативность умножения матриц (см. 10.4), получаем

(AB)(B^-1A^-1) = A(BB^-1)A^-1 = AEA^-1 = AA^-1 = E ,

(B^-1A^-1)(AB) = B^-1(A^-1A)B = B^-1EB = B^-1B = E. ►

Теорема 11.4. Если матрица A порядка n имеет обратную, то и транспонированная матрица A^T имеет обратную, причем (A^T)^-1 = (A^-1)^T.

◄ Нужно убедиться, что A^T(A^-1)^T = E и (A^-1)^TA^T = E. Используя свойство произведения матриц относительно операции транспонирования, имеем

A^T(A^-1)^T = (А^-1 A)^T = E^T = E, (A^-1)^T = (AA^-1)^T = E^T = E. ►