Линейные операции и их свойства

Обсуждение векторных операций начнем с двух из них - сложения векторов и умножения вектора на число. Эти операции часто объединяют общим термином линейные операции.

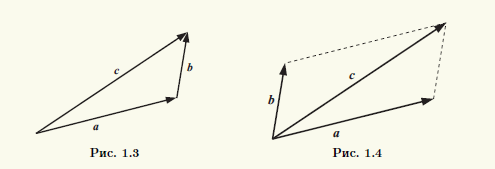
Определение 1.5. Суммой а + b двух векторов а и b называют вектор с, построенный по следующему правилу треугольника. Совместим начало вектора b с концом вектора а. Тогда суммой этих векторов будет вектор с, начало которого совпадает с началом а, а конец - с концом b (рис. 1.3).

Замечание 1.2. Наряду с правилом треугольника существует правило параллелограмма. Выбрав для векторов а и b общее начало, строим на этих векторах параллелограмм. Тогда диагональ параллелограмма, выходящая из общего начала векторов, определяет их сумму (рис. 1.4). Отметим, что если векторы а и b коллинеарны, то их сумму по правилу параллелограмма определить нельзя, а правило треугольника применимо и в этом случае.

Замечание 1.3. В определении 1.5 существует произвол в выборе точки приложения векторов, но результаты, получаемые с различными точками приложения, равны между собой. #

1°. Сложение векторов коммутативно: а + b = b + а.

◄ Если складываемые векторы неколлинеарны, то свойство непосредственно вытекает из правила параллелограмма, так как в этом правиле порядок векторов не играет роли. Если же векторы коллинеарны, то их сложение сводится к сложению или вычитанию их длин в зависимости от того, являются ли складываемые векторы однонаправленными или противоположно направленными. ►

2°. Сложение векторов ассоциативно: (а + b) + с = а + (b + с).

◄ Доказать это свойство проще всего при помощи правила треугольника. Выберем в качестве начала вектора а точку A (рис. 1.5), и пусть а = AB. Совместим начало вектора b с точкой В,и пусть b = BC. Наконец, начало вектора с совместим с концом C вектора b, и пусть тогда с = CD.

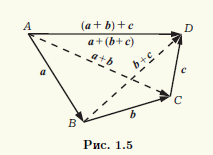
Непосредственно из построения получаем

AD = AB + BD = AB + (BC + CD) = а + (b + с),

AD = AC + CD = (AB + BC) + CD) = (а + b) + с,

т.е. геометрический вектор AD изображает и левую часть доказываемого равенства, и правую. ►

3°. Существует такой вектор 0, что для любого вектора а выполняется равенство а + 0 = а.

◄ Действительно, непосредственной проверкой можно убедиться, что указанному условию удовлетворяет нулевой вектор. Проверку удобно проводить при помощи правила треугольника. ►

4°. Для любого вектора а существует такой вектор b, что а + b = 0.

◄ Действительно, таким является вектор (-а), противоположный к вектору а, т.е. вектор, коллинеарный а, той же длины, что и а, но противоположно направленный. Если в качестве точки приложения этого вектора выбрать конец вектора а, то конец противоположного вектора совпадет с началом вектора а. Согласно правилу треугольника, суммой векторов а и (-а) будет вектор с совпадающими началом и концом, т.е. нулевой вектор. ►

5°. Для любых векторов а и b существует такой вектор х, что а + x = b. При этом вектор х определен однозначно.

◄ Указанному условию удовлетворяет вектор (-а) + b, так как с учетом свойств 2°-4°

а + х = а + ((-а) + b) = (а + (-а)) + b = 0 + b = b.

Если вектор х удовлетворяет равенству а + х = b, то, прибавив слева к обеим частям последнего равенства вектор (-а), получим с учетом свойств 1°, 2°, что х = (-а) + b. Действительно,

(-а) + (а + х) = ((-а) + а) + х = 0 + х = х = (-а) + b.

Значит, вектор х определен однозначно. ►

Свойство 5° позволяет ввести операцию вычитания векторов.

Определение 1.6. Разностью b - а двух векторов а и b называют такой вектор х, что а + х = b.

С алгебраической точки зрения переход от а + х = b к х = b - а (в соответствии с определением 1.6) означает, что при переносе вектора в другую часть равенства перед ним надо менять знак.

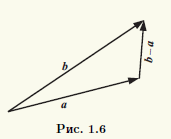
Практически для вычисления разности векторов можно воспользоваться правилом треугольника. Совместим начала векторов а и b, тогда вектор с началом в конце вектора а и концом, совпадающим с концом b, равен разности b - а этих векторов (рис. 1.6).

Операцию вычитания векторов также относят к линейным, так как она определяется операцией сложения и является обратной сложению.

Определение 1.7. Произведением вектора а на число λ называют вектор λа, коллинеарный вектору а, с длиной |λ| |а|, однонаправленный с а при λ > 0 и противоположно направленный при λ < 0.

Замечание 1.4. Если λ = 0, то, согласно этому определению, вектор 0а должен иметь длину 0 |а| = 0, т.е. должен быть нулевым вектором. Поэтому, хотя остальные характеристики и не определены (коллинеарность, направленность), произведение вектора на число 0 задано однозначно: 0а есть нулевой вектор.

Пример 1.2. Произведение вектора а на число -1 есть вектор, противоположный к а, т.е. (-1)а = (-а). #

Операция умножения вектора на число обладает свойством ассоциативности, а совместно с операцией сложения она удовлетворяет двум свойствам дистрибутивности.

6°. Умножение вектора на число ассоциативно: (λμ)а = λ( μа).

◄ Действительно, обе части равенства представляют собой векторы, коллинеарные исходному вектору а. Поэтому равенство будет верным, если совпадут длины векторов и их направления. Равенство длин векторов очевидно. Если числа λ и μ имеют один и тот же знак, то векторы в обеих частях будут однонаправлены с вектором а. Если же λ и μ имеют противоположные знаки, то оба вектора в равенстве являются противоположно направленными по отношению к а. Итак, в любом случае в равенстве стоят векторы одного направления и одинаковой длины, т.е. равные векторы. ►

7°. Умножение вектора на число дистрибутивно относительно векторов: λ(а + b) = λа + λb.

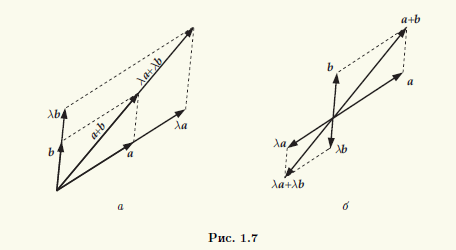
◄ При λ = 0 свойство очевидно, так как в этом случае слева будет нулевой вектор (произведение вектора на число 0), а справа - сумма двух нулевых векторов. Если λ ≠ 0, свойство вытекает из правила параллелограмма и свойств подобных параллелограммов. На рис. 1.7 представлены случаи: а) λ > 0; б) λ < 0. ►

8°. Умножение вектора на число дистрибутивно относительно чисел: (λ + μ)а = λа + μа.

В указанном равенстве - три коллинеарных вектора. Поэтому доказательство сводится к подсчету длин векторов, которым присвоены знаки, учитывающие направление. Если λ и μ имеют положительные знаки, то все три вектора в равенстве имеют одно направление, совпадающее с направлением вектора а. При сложении этих векторов справа складываются их длины, а доказываемое равенство равносильно следующему: (λ + μ) |а| = λ |а| + μ |а|. Случай, когда λ и μ отрицательны, аналогичен.

Пусть λ и μ имеют противоположные знаки. Для определенности будем считать, что λ > 0, μ < 0. Противоположный случай сводится к этому заменой обозначений и учетом коммутативности сложения чисел и векторов. Если λ > 0, μ < 0, то при сложении векторов λа и μа вычитаются их длины, так как складываются векторы противоположного направления.

Получаемый при этом вектор будет однонаправленным с а при |λ| > | μ| и противоположно направленным при |λ| < |μ|. Его длина, согласно определению произведения вектора на число, равна |λ + μ||а|. Учитывая направление этого вектора, заключаем, что он равен (λ + μ)а, т.е. доказываемое равенство верно и при противоположных знаках коэффициентов λ и μ.

Наконец, отметим тривиальный случай, когда один из коэффициентов λ и μ равен нулю. Например, если μ = 0, то равенство (λ + μ) |а| = λ|а| + μ|а| сводится к равенству (λ + 0)а = λа + 0а, вытекающему из свойства 3° и определения 1.7. ►