Приведение к простейшему виду уравнения центральной линии второго порядка
Решение задачПусть дано уравнение
Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0, (1)
определяющее центральную линию второго порядка (δ = AC - B2 ≠ 0). Перенося начало координат в центр S(x0; у0) этой линии и
преобразуя уравнение (1) по формулам
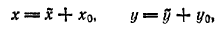
получим:
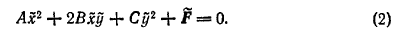
Для вычисления 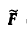 можно пользоваться формулой
можно пользоваться формулой
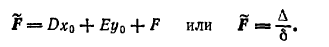
Дальнейшее упрощение уравнения (2) достигается при помощи преобразования координат
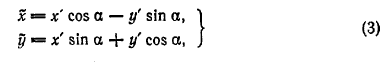
соответствующего повороту осей на угол α.
Если угол α выбран так, что
В tg2α - (С - A) tgα - В = 0, (4)
то в новых координатах уравнение линии примет вид
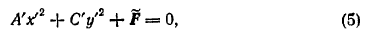
где А' ≠ 0, С' ≠ 0.
Замечание. Уравнение (4) позволяет определить tgα, тогда как в формулах (3) участвуют sinα и cosα. Зная tgα, можно найти sinα и cosα по формулам тригонометрии
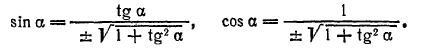
Между коэффициентами уравнений (1) и (5) существуют важные соотношения:
А'С' = АС - В2, А' + С' = А + С,
которые позволяют определить коэффициенты А' и С', не проводя преобразования координат.
Уравнение второй степени называется эллиптическим, если δ > 0, гиперболическим, если δ < 0, и параболическим, если δ = 0. Уравнение центральной линии может быты только эллиптическим или гиперболическим.
Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (т. е. определяет единственную точку), либо мнимого эллипса (в этом случае уравнение не определяет никакого геометрического образа).
Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную гиперболу (т. е. пару пересекающихся прямых).
673. Определить тип каждого из следующих уравнений *); каждое из них путем параллельного переноса осей координат привести к простейшему виду; установить, какие геометрические образы они определяют, и изобразить на чертеже расположение этих образов относительно старых и новых осей координат:
*) То есть установить, какие из них являются эллиптическимим, какие гиперболическими и какие параболическими
1) 4х2 + 9у2 - 40x + 36y + 100 = 0;
2) 9x2 - 16y2 - 54x - 64y - 127 = 0;
3) 9x 2 + 4y2 + 18х - 8y + 49 = 0;
4) 4x2 - у2 - 2y + 3 = 0;
5) 2х2 + 3y2 + 8х - 6y + 11 = 0.
674. Каждое из следующих уравнений привести к простейшему виду? определить тип каждого из них; установить, какие геометрические образы они определяют, и изобразить на чертеже расположение этих образов относительно старых и новых осей координат:
1) 32x2 + 52xy - 7y2 + 180 = 0;
2) 5x2 - 6xy + 5y2 - 32 = 0;
3) 17x2 - 12xy + 8y2 = 0;
4) 5x2 + 24xy - 5y2 = 0;
5) 5x2 - 6xy + 5y2 + 8 = 0.
675. Определить тип каждого из следующих уравнений при помощи вычисления дискриминанта старших членов:
1) 2х2 + 10xy + 12y2 - 7x + 18y - 15 = 0;
2) З*2 - 8xy + 7y2 + 8x - 15y + 20 = 0;
3) 25x2 - 20xy + 4y2 - 12x + 20у - 17 = 0;
4) 5x2 + 14xy + 11y2 + 12x - 7y + 19 = 0;
5) x2 - 4xy + 4y2 + 7x - 12 = 0;
6) 3x2 - 2xy - 3y2 + 12y - 15 = 0.
676. Каждое из следующих уравнений привести к каноническому виду; определить тип каждого из них; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной координатной системы, оси других ко-ординатных систем, которые вводятся по ходу решения, и геометрический образ, определяемый данным уравнением:
1) 3х2 + 10хy + 3y2 - 2х - 14у- 13 = 0;
2) 25x2 - 14ху + 25у2 + 64х - 64y - 224 = 0;
3) 4ху + 3у2 + 16х + 12у - 36 = 0;
4) 7х2+ 6ху - y2 + 28х + 12у + 28 = 0;
5) 19х2 + 6ху + 11 у2 + 38х + 6у + 29 = 0;/p>
6) 5х2 - 2ху + 5y2 - 4х + 20у + 20 = 0.
677. То же задание, что и в предыдущей задаче, выполнить для уравнений
1) 14х2 + 24ху + 21y2 - 4х + 18y - 139 = 0;
2) 11х2 - 20ху - 4у2 - 20х - 8у + 1 = 0;
3) 7х2 + 60хy + 32y2 - 14х - 60y + 7 = 0;
4) 50х2 - 8хy + 35y2 + 100х - 8y + 67 = 0;
5) 41х2 + 24ху + 34y2 + 34х - 112у + 129 = 0;
6) 29х2 - 24ху + 36y2 + 82х - 96y - 91 = 0;
7) 4х2 + 24ху + 11у2 + 64х + 42y + 51 = 0;
8) 41х2 + 24хy + 9у2 + 24х + 18y - 36 = 0.
678. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет эллипс, и найти величины его полуосей:
1) 41х2 + 24ху + 9у2 + 24х + 18y - 36 = 0;
2) 8х2 + 4ху + 5y2 + 16х + 4у - 28 = 0;
3) 13х2 + 18хy + 37y2 - 26х - 18y + 3 - 0;
4) 13х2 + 10хy + 13у2 + 46х + 62у +13 = 0.
679. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет единственную точку (вырожденный эллипс), и найти ее координаты:
1) 5х2 - 6ху + 2у2 - 2х + 2 = 0;
2) х2 + 2хy + 2у2 + 6y + 9 = 0;
3) 5х2 + 4ху + у2 - 6х - 2у + 2 = 0;
4) х2 - 6ху + 10у2 + 10х - 32у + 26 = 0.
680. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет гиперболу, и найти величины ее полуосей:
1) 4х2 + 24ху + 11y2 + 64x + 42y + 51 = 0;
2) 12х2 + 26xy + 12y2 - 52х - 48y + 73 = 0;
3) 3x2 + 4xy - 12х + 16 = 0;
4) х2 - 6ху - 7у2 + 10x - 30у + 23 = 0.
681. Не проводя преобразования координат, устано-вить, что каждое из следующих уравнений определяет пару пересекающихся прямых (вырожденную гиперболу), и найти их уравнения:
1) 3x2 + 4xy + y2 - 2х - 1 = 0;
2) х2 - 6xy + 8у2 - 4у - 4 = 0;
3) х2 - 4xy + 3y2 = 0;
4) х2 + 4ху + 3у2 - 6х - 12у + 9 = 0.
682. Не проводя преобразования координат, устано-вить, какие геометрические образы определяются сле-дующими уравнениями:
1) 8х 2 - 12xy + 17y2 + 16x - 12y -3 = 0;
2) 17х2 - 18xy - 7y2 + 34x - 18u + 7 = 0;
3) 2х2 + 3xy - 2y2 + 5х + 10y = 0;
4) 6х2 - 6xy + 9y2 - 4x + 18y + 14 = 0;
5) 5х2 - 2xy + 5y2 - 4х + 20у + 20 = 0.
683. Для любого эллиптического уравнения доказать, что ни один из коэффициентов A и С не может обращаться в нуль и что они суть числа одного знака.
684. Доказать, что эллиптическое уравнение второй степени (δ > 0) определяет эллипс в том и только в том случае, когда А и Δ суть числа разных знаков.
685. Доказать, что эллиптическое уравнение второй степени (δ > 0) является уравнением мнимого эллипса в том и только в том случае, когда А и Δ суть числа одинаковых знаков.
686. Доказать, что эллиптическое уравнение второй степени (δ > 0) определяет вырожденный эллипс (точку) в том и только в том случае, когда Δ = 0.
687. Доказать, что гиперболическое уравнение второй степени (δ < 0) определяет гиперболу в том и только в том случае, когда Δ ≠ 0.
688. Доказать, что гиперболическое уравнение второй степени (δ < 0) определяет вырожденную гиперболу (пару пересекающихся прямых) в том и только в том случае, когда Δ = 0.