Гипербола
Решение задачГиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина; указанная разность берется по абсолютному значению и обозначается обычно через 2а, Фокусы гиперболы обозначают буквами F1 и F2, расстояние между ними - через 2с. По определению гиперболы 2а < 2с, или а < с.
Пусть дана гипербола. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид
х2/a2 + y2/b2 = 1, (1)
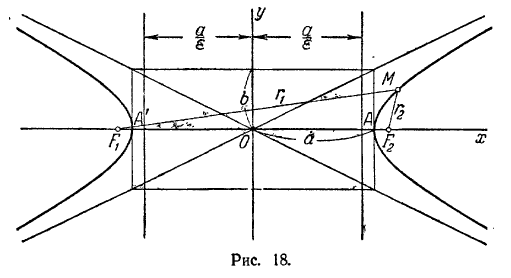
где b = √(с2 - а2). Уравнение вида (I) называется каноническим уравнением гиперболы При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат -ее центром симметрии (рис. 18). Оси симметрии гиперболы называются просто ее осями, центр симметрии-центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На рис. 18 вершины гиперболы суть точки А' и А.
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.
Отрезки длиной 2а и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют ее осями. Диагонали основного прямоугольника (неограниченно продолженные) являются асимптотами гиперболы; их уравнения суть:
y = b/a x, y = - b/a x
Уравнение
- x2/a2 + y2/b2 = 1 (2)
определяет гиперболу, симметричную относительно координатных осей с фокусами на оси ординат; уравнение (2),как и уравнение (1), называется каноническим уравнением гиперболы; в этом случае постоянная разность расстояний от произвольной точки гиперболы до фокусов равна 2b.
Две гиперболы, которые определяются уравнениями
x2/a2 - y2/b2 = 1, - x2/a2 + y2/b2 = 1
в одной и той же системе координат, называются сопряженными.
Гипербола с равными полуоясми (а = b) называется равносторонней,; ее каноническое уравнение имеет вид
х2 - у2 = а2 или - х2 + у2 = а2.
Число
ε = c/a
где а - расстояние от центра гиперболы до ее вершины, называется эксцентриситетом гиперболы. Очевидно, для любой гиперболы ε > 1. Если М(х; у) - произвольная точка гиперболы, то отрезки F1М и F2M (см. рис. 18) называются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам
r1 = εх + а, r2 = εх - а,
фокальные радиусы точек левой ветви - по формулам
r1 = -εх - а, r2 = -εх + а
Если гипербола задана уравнением (1), то прямые, определяемые уравнениями
x = -a/ε, x = a/ε
называются ее директрисами (см. рис. 18). Если гипербола задана уравнением (2), то директрисы определяются уравнениями
x = -b/ε, x = b/ε
Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки гиперболы до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету гиперболы:
r/d = ε
515. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:
1) ее оси 2а = 10 и 2b = 8;
2) расстояние между фокусами 2с = 10 и ось 2b = 8;
3) расстояние между фокусами 2с = 6 и эксцентриситет ε = 3/2;
4) ось 2а = 16 и эксцентриситет ε = 5/4;
5) уравнения асимптот у = ±4/3х и расстояние между фокусами 2с = 20;
6) расстояние между директрисами равно 22 2/13 и расстояние между фокусами 2с = 26; 39
7) расстояние между директрисами равно 32/5 и ось 2b = 6;
8) расстояние между директрисами равно 8/3 и эксцентриситет ε = 3/2;
9) уравнения асимптот у = ± 3/4 х и расстояние между директрисами равно 12 4/5.
516. Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что:
1) ее полуоси а = 6, b = 18 (буквой а мы обозначаем полуось гиперболы, расположенную на оси абсцисс);
2) расстояние между фокусами 2с = 10 и эксцеитриситет ε = 5/3; оч и. 12
3) уравнения асимптот у = ±12/5х и расстояние между вершинами равно 48;
4) расстояние между директрисами равно 7 1/7 и эксцентриситет ε = 7/5;
5) уравнения асимптот у = ± 4/3x и расстояние между директрисами равно 6 2/5.
517. Определить полуоси а и b каждой из следующих гипербол:
1) x2/9 - y2/4 = 1; 2) x2/16 - y2 = 1; 3) x2 - 4y2 = 16;
4) x2 - y2 = 1; 5) 4x2 - 9y2 = 25; 6) 25x2 -16y2 = 1;
7) 9x2 - 64y2 = 1.
518. Дана гипербола 16x2 - 9y2 = 144. Найти: 1) полуоси а и b; 2) фокусы; 3) эксцентриситет; 4) уравнения асимптот; 5) уравнения директрис.
519. Дана гипербола 16x2 - 9у2 = -144. Найти: 1) полуоси a и b; 2) фокусы; 3) эксцентриситет; 4) уравнения асимптот; 5) уравнения директрис.
520. Вычислить площадь треугольника, образованного асимптотами гиперболы x2/4 - y2/9 = 1 и прямой 9x + 2y - 24 = 0.
521. Установить, какие линии определяются следующими уравнениями:
1) y = +2/3√(x2 - 9); 2) y = -3√(x2 + 1)
3) x = -4/3√(y2 + 9); 4) +2/5√(x2 + 25)
Изобразить эти линии на чертеже.
522. Дана точка M1(l0; - √5) на гиперболе - x2/80 - y2/20 = 1. Составить уравнения прямых, на которых лежат фокальные радиусы точки M1.
523. Убедившись, что точка M1(-5; 9/4) лежит на гилерболе x2/16 - y2/9 = 1, определить фокальные радиусы точки M1.
524. Эксцентриситет гиперболы ε = 2, фокальный ра-диус ее точки М, проведенный из некоторого фокуса, равен 16. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
525. Эксцентриситет гиперболы ε = 3, расстояние от точки, М гиперболы до директрисы равно 4. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.
526. Эксцентриситет гиперболы ε = 2, центр ее лежит в начале координат, один из фокусов F(12; 0). Вычислить расстояние от точки M1 гиперболы с абсциссой, равной 13, до директрисы, соответствующей заданному фокусу.
527. Эксцентриситет гиперболы ε = 3/2, центр ее лежит в начале координат, одна из директрис дана уравнением х = -8. Вычислить расстояние от точки M1 гиперболы с абсциссой, равной 10, до фокуса, соответствующего заданной директрисе.
528. Определить точки гиперболы - x2/64 - y2/36 = 1, расстояние которых до правого фокуса равно 4,5.
529. Определить точки гиперболы x2/9 - y2/16 = 1, расстояние которых до левого фокуса равно 7.
530. Через левый фокус гиперболы x2/144 - y2/25 = 1 про-веден перпендикуляр к ее оси, содержащей вершины. Определить расстояния от фокусов до точек пересечения этого перпендикуляра с гиперболой.
531. Пользуясь одним циркулем, построить фокусы гиперболы x2/16 - y2/25 = 1 (считая, что оси координат изображены и масштабная единица задана).
532. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны:
1) точки М1(6; -1) и М2(-8; 2√2) гиперболы;
2) точка M1(-5; 3) гиперболы и эксцентриситет ε = √2;
3) точка M1(9/2;-l) гиперболы и уравнения асимптот у = ± 2.3х;
4) точка M1(-3 ; 5.2) гиперболы и уравнения директрис х = ± 4/3;
5) уравнения асимптот у = ±-3/4х и уравнения директрис х = ± 16/5
533. Определить эксцентриситет равносторонней гиперболы.
534. Определить эксцентриситет гиперболы, если отрезок между ее вершинами виден из фокусов сопряженной гиперболы под углом в 60°.
535. Фокусы гиперболы совпадают с фокусами эллипса x2/25 + y2/9 = 1. Составить уравнение гиперболы, если ее эксцентриситет ε = 2.
536. Составить уравнение гиперболы, фокусы которой лежат в вершинах эллипса x2/100 + y2/64 = 1, а директрисы проходят через фокусы этого эллипса.
537. Доказать, что расстояние от фокуса гиперболы x2/a2 - y2/b2 = 1 до ее асимптоты равно b.
538. Доказать что произведение расстояний от любой точки гиперболыx x2/a2 - y2/b2 = 1 до двух ее асимптот есть величина постоянная, равная a2b2/(a2 + b2)
539. Доказать, что площадь параллелограмма, ограниченного асимптотами гиперболы x2/a2 - y2/b2 = 1 и прямыми, проведенными через любую ее точку параллельно асимптотам, есть величина постоянная, равная ab/2.
540. Составить уравнение гиперболы, если известны ее полуоси а и b, центр С(х0;у0) и фокусы расположены на прямой: 1) параллельной оси Ох; 2) параллельной оси Оу.
541. Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты ее центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис:
1) 16x2 - 9у2 - 64x - 54у - 161 =0;
2) 9x2 - 16у2 + 90x + 32y - 367 = 0;
3) 16x2 - 9у2 - 64x - 18у + 199 = 0.
542. Установить, какие линии определяются следующими уравнениями:
1) у = - 1 + 2/3√(x2 - 4x - 5);
2) у = 7- 3/2√(х2 - 6х + 13);
3) x = 9 - 2√(y2 + 4y + 8);
4) Х = 5 + 3/4√(y2 + 4y - 12).
Изобразить эти линии на чертеже.
543. Составить уравнение гиперболы, зная, что:
1) расстояние между ее вершинами равно 24 и фокусы суть F1(-10;2), F2(16; 2);
2) фокусы суть F1(3;4), F2(-3; -4) и расстояние между директрисами равно 3,6;
3) угол между асимптотами равен 90° и фокусы суть F1(4; -4), F1(- 2;2).
544. Составить уравнение гиперболы, если известны ее эксцентриситет ε = 5/4, фокус F (5; 0) и уравнение соответствующей директрисы 5х - 16 = 0.
545. Составить уравнение гиперболы, если известны ее эксцентриситет е - фокус F(0; 13) и уравнение соответствующей директрисы 13y - 144 = 0.
546. Точка А (-3; - 5) лежит на гиперболе, фокус которой F (-2;-3), а соответствующая директриса дана уравнением x + 1 = 0. Составить уравнение этой гиперболы.
547. Составить уравнение гиперболы, если известны ее эксцентриситет ε = √5, фокус F(2;-3) и уравнение соответствующей директрисы Зх - у + 3 = 0.
548. Точка M1(1; 2) лежит на гиперболе, фокус которой F(-2; 2), а соответствующая директриса дана уравнением 2х - у - 1 = 0. Составить уравнение этой гиперболы.
549. Дано уравнение равносторонней гиперболы х2 - у2 = а2. Найти ее уравнение в новой системе, приняв за оси координат ее асимптоты.
550. Установив, что каждое из следующих уравнений определяет гиперболу, найти для каждой из них центр, полуоси, уравнения асимптот и построить их на чертеже: 1) ху = 18; 2) 2ху - 9 = 0; 3) 2ху + 25 = 0.
551. Найти точки пересечения прямой 2x - y - 10 = 0 и гиперболы х2/20 - y2/5 = 1.
552. Найти точки пересечения прямой 4х - 3y - 16 = 0 и гиперболы х2/25 - y2/16 = 1.
553. Найти точки пересечения прямой 2x - y + 1 = 0 и гиперболы х2/9 - y2/4 = 1.
554. В следующих случаях определить, как расположена прямая относительно гиперболы: пересекает ли, касается или проходит вне ее:
1) x - y - 3 = 0, х2/12 - y2/3 = l;
2) x - 2y + 1 = 0, х2/16 - y2/9 = l;
555. Определить, при каких значениях m прямая y = 5/2x + m
1) пересекает гиперболу x2/9 - y2/36 = 1; 2) касается ее;
3) проходит вне этой гиперболы.
556. Вывести условие, при котором прямая у = kx + m касается гиперболы х2/a2 - y2/b2 = 1.
557. Составить уравнение касательной к гиперболе х2/a2 - y2/b2 = 1 в ее точке Af, (*,; #i).
558. Доказать, что касательные к гиперболе, про-веденные в концах одного и того же диаметра, параллельны.
559. Составить уравнения касательных к гиперболе х2/20 - y2/5 = 1, перпендикулярных к прямой 4x + Зy - 7 = 0.
560. Составить уравнения касательных к гиперболе x2/16 - y2/64 = 1, параллельных прямой 10x - 3y + 9 = 0.
561. Провести касательные к гиперболе x2/16 - y2/8 = - 1 параллельно прямой 2x + 4y - 5 = 0 и вычислить расстояние d между ними.
562. На гиперболе x2/24- y2/18 = 1 найти точку М1, ближайшую к прямой Зx + 2y + 1 = О, и вычислить расстояние d от точки Mx до этой прямой.
563. Составить уравнение касательных к гиперболе х2 - y2 = 16, проведенных из точки A(- 1; -7).
564. Из точки С(1;-10) проведены касательные к гиперболе x2/8 - y2/32 = 1. Составить уравнение хорды, соединяющей точки касания.
565. Из точки Р(1; -5) проведены касательные к гиперболе x2/3 - y2/5 = 1. Вычислить расстояние d от точки Р до хорды гиперболы, соединяющей точки касания.
566. Гипербола проходит через точку А(√6; 3) и касается прямой 9x + 2у - 15 == 0. Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат.
567. Составить уравнение гиперболы, касающейся двух прямых: 5x - 6y - 16 = 0, 13x - 10y - 48 = 0, при условии, что ее оси совпадают с осями координат.
568. Убедившись, что точки пересечения эллипса x2/3 - y2/5 = 1 и гиперболы x2/12 - y2/3 = 1 являются вершинами прямоугольника, составить уравнения его сторон.
569. Даны гиперболы x2/a2 - y2/b2 = 1 и какая-нибудь ее касательная: Р - точка пересечения касательной с осью Ox, Q - проекция точки касания на ту же ось. Доказать, что ОР • OQ = а2.
570. Доказать, что фокусы гиперболы расположены по разные стороны от любой ее касательной.
571. Доказать, что произведение расстояний от фокусов до любой касательной к гиперболе x2/a2 - y2/b2 = 1 есть величина постоянная, равная b2.
572. Прямая 2x - y - 4 == 0 касается гиперболы, фокусы которой находятся в точках F1 (-3; 0) и F2 (3;0). Составить уравнение этой гиперболы.
573. Составить уравнение гиперболы, фокусы кото-рой расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к гиперболе 15x + 16y - 36 = 0 и расстояние между ее вершинами 2а = 8.
574. Доказать, что прямая, касающаяся гиперболы в некоторой точке М, составляет равные углы с фокальными радиусами F1M, F2M и проходит внутри угла F1MF2. Х^
575. Из правого фокуса гиперболы x2/5 - y2/4 = 1 под углом α(π < α < 3/2π) к оси Ох направлен луч света. Известно, что tgα = 2. Дойдя до гиперболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
576. Доказать, что эллипс и гипербола, имеющие общие фокусы, пересекаются под прямым углом.
577. Коэффициент равномерного сжатия плоскости к оси Ох равен 4/3 . Определить уравнение линии, в которую при этом сжатии преобразуется гипербола x2/16 - y2/9 = 1. Указание. См. задачу 509.
578. Коэффициент равномерного сжатия плоскости к оси Оу равен 4/5. Определить уравнение линии, в которую при этом сжатии преобразуется гипербола x2/25 - y2/9 = 1.
579. Найти уравнение линии, в которую преобразуется гипербола х2 - у2 = 9 при двух последовательных равномерных сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плос- кости к осям Ох и Оу соответственно равны 2/3 и 5/3.
580. Определить коэффициент q равномерного сжатия плоскости к оси Ох, при котором гипербола - x2/25 - y2/36 = 1 преобразуется в гиперболу x2/25 - y2/16 = 1.
581. Определить коэффициент q равномерного сжатия плоскости к оси Оу, при котором гипербола x2/4 - y2/9 = 1 преобразуется в гиперболу x2/16 - y2/9 = 1.
582. Определить коэффициенты q1 и q2 двух последовательных равномерных сжатий плоскости к осям Ох и Оу, при которых гипербола x2/49 - y2/16 = 1 преобразуется в гиперболу x2/25 - y2/64 = 1.