Общее уравнение прямой. Уравнение прямой е угловым коэффициентом.
Решение задачВ декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.
Уравнение вида
Ах + Ву + С = 0 (1)
называется общим уравнением прямой.
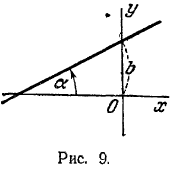
Угол α, определяемый, как показано на рис, 9, называется углом наклона прямой к оси Ох. Тангенс угла йаклонД' прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:
k = tgα.
Уравнение у = kx + b называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.
Если прямая задана общим уравнением
Ах + By + С - О,
То ее угловой коэффициент определяется по формуле
k = -A/B.
Уравнение у - y0 = k(x - х0) является уравнением прямой, которая проходит через точку M0(x0; y0) и имеет угловой коэффициент k.
Если прямая проходит через точки М1(х1; у1) и М2(х2; y2) то ее угловой коэффициент определяется по формуле
k = (y2 - y1)/(x2 - x1)
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)
является уравнением прямой, проходящей через две точки
M1(x1,y1) и М2(х2; у2).
Если известны угловые коэффициенты двух прямых k1 и k2, то один из углов φ между этими прямыми определяется по формуле
tgφ = (k2 - k1)/(1 + k1k2)
Признаком параллельности двух прямых является равенство их угловых коэффициентов
k1 = k2
Признаком перпендикулярности двух прямых является соотношение
k1k2 = -1 или k2 = -1/k1
Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.
210. Определить, какие из точек М1(3; 1); 1), М2(2; 3), M3(6; 3), М4(-3; -3), М5(3; -1), М6(-2; 1) лежат на прямой 2х- 3у - 3 = 0 и какие не лежат на ней.
211. Точки P1, Р2, Р3, P4 и Р5 расположены на прямой 3x - 2у - 6 = 0; их абсциссы соответственно равны числам; 4, 0, 2, -2 и -6. Определить ординаты этих точек.
212. Точки Q1, Q2, Q3, Q4 и Q5 расположены на прямой х - 3y + 2 = 0; их ординаты соответственно равны числам; 1, 0, 2, -1, 3. Определить абсциссы этих точек.
213. Определить точки пересечения прямой 2x - Зy - 12 = 0 с координатными осями и построить эту прямую на чертеже.
214. Найти точку пересечения двух прямых Зх - 4y - 29 = 0, 2х + 5у + 19 = 0.
215. Стороны АВ, ВС и АС треугольника ABC даны соответственно уравнениями *) 4х + Зу - 5 = 0, х - Зу + 10 = 0, x - 2 = 0. Определить координаты его вершин.
216. Даны уравнения двух сторон параллелограмма 8x + 3y + 1 = 0, 2х + у - 1 = 0 и уравнение одной из его диагоналей Зх + 2y + 3 = 0. Определить координаты вершин этого параллелограмма. •
*) Здесь и везде в дальнейшем под уравнением сторон мы будем понимать уравнения прямых, на которых лежат стороны.217. Стороны треугольника лежат на прямых х + 5y - 7 = 0, Зх - 2у - 4 = 0, 7х + у + 19 = 0. Вычислить его площадь S.
218. Площадь треугольника S = 8 кв. ед.; две его вершины суть точки A(1; -2) и В(2;3), а третья вершина С лежит на прямой 2х + у - 2 = 0. Определить координаты вершины С.
219. Площадь треугольника S = 1,5 кв. ед., две его вершины суть точки А (2; -3) и В(3; -2); центр тяжести этого треугольника лежит на прямой Зх - у - 8 = 0. Определить координаты третьей вершины С.
220. Составить уравнение прямой и построить прямую на чертеже, зная ее угловой коэффициент k и отрезок b, отсекаемый ею на оси Оу.
1) k = 2/3, b = 3; 2) k = 3, b = 0; 3) k = 0, b = - 2;
4) k = - 3/4, b = 3; 5) k = - 2, b = -5;
6) k= -1/3, b = 2/3.
221. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Оу, для каждой из прямых:
1) 5х - у + 3 = 0; 2) 2х + 3у - 6 = 0;
3) 5х + 3у + 2 = 0; 4) Зх + 2у = 0; 5) у - 3 = 0.
222. Дана прямая 5х + 3у - 3 = 0. Определить угловой коэффициент к прямой:
1) параллельной данной прямой;
2) перпендикулярной к данной прямой.
223. Дана прямая 2х + Зу + 4 = 0. Составить уравнение прямой, проходящей через точку М0(2; 1):
1) параллельно данной прямой;
2) перпендикулярно к данной прямой;
224. Даны уравнения двух сторон прямоугольника 2х - 3y +5 = 0, Зх + 2у - 7 = 0 и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого прямоугольника.
225. Даны уравнения двух сторон прямоугольника х - 2у = 0, х - 2y + 15 = 0 и уравнение одной из его диагоналей 7x + у - 15 = 0. Найти вершины прямоугольника.
226. Найти проекцию точки Р(-6; 4) на прямую 4х - 5y + 3 = 0,
227. Найти точку Q, симметричную точке Р(-5; 13) относительно прямой 2х - 3у - 3 = 0.
228. В каждом из следующих случаев составить уравнение прямой, параллельной двум данным прямым и проходящей посередине между ними:
1) Зх - 2у - 1 = 0, Зx - 2у - 13 = 0;
2) 5х + у + 3 = 0, 5x + у - 17 = 0;
3) 2х + 3у - 6 = 0, 4x + 6у + 17 = 0;
4) 5х + 7у + 15 = 0, 5х + 7у + 3 = 0;
5) Зх - 15у- 1 = 0, х - 5у - 2 = 0.
229. Вычислить угловой коэффициент k прямой, проходящей через две данные точки: а) M1(2; -5), М2(3; 2);б) Р(-3; 1), Q (7; 8); в) Л (5; -3), Я(-1; 6).
230. Составить уравнения прямых, проходящих через вершины треугольника Ф/ (5; -4), В(-1; 3), С(-3; -2) параллельно противоположным сторонам.
231. Даны середины сторон треугольника: M1(2; 1), M2(5; 3) и М3(3; -4). Составить уравнение его сторон.
232. Даны две точки: Р(2; 3) и Q(-1; 0). Составить уравнение прямой, проходящей через точку Q перпен-дикулярно к отрезку PQ.
233. Составить уравнение прямой, если точка Р(2;3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.
234. Даны вершины треугольника M1(2; 1); M1(-1; -1) и М3(3; 2). Составить уравнения его высот;
235. Стороны треугольника даны уравнениями 4х - у - 7 = 0, х + Зу - 31=0, х + 5у - 7. = 0. Определить точку пересечения его высот.
236. Даны вершины треугольника A(1; -1 ),В(-2; 1)' и С(3; 5). Составить уравнение перпендикуляра, опущенного из вершины A на медиану, проведенную из вершины В.
237. Даны вершины треугольника A(2; -2), В(3; -5) и С(5; 7). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннею угла при вершине A.
238. Составить уравнения сторон и медиан треугольника с вершинами A(3: 2), B(5; -2), С(1; 0).
239. Через точки М1(-1; 2) и М2(2; 3) проведена прямая. Определить точки пересечения этой прямой с осями координат.
240. Доказать, что условие, при котором три точки M1(x1; y1), М2(x2; y2) и М3(x3; y3) лежат на одной прямой, может быть записано в следующем виде:
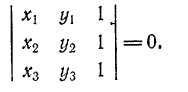
241. Доказать, что уравнение прямой, проходящей через две данные точки M1(x1; y1) и М2(x2; y2), может быть записано в следующем виде:
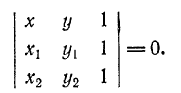
242. Даны последовательные вершины выпуклого четырехугольника А (-3; 1), В(3; 9), С (7; 6) и D(-2; -6). Определить точку пересечения его диагоналей.
243. Даны две смежные вершины A(-3; -1) и В(2; 2) параллелограмма ABCD и точка Q(3; 0) пересечения его диагоналей Составить уравнения сторон этого параллелограмма.
244. Даны уравнения двух сторон прямоугольника 5x + 2y - 7 = 0, 5х + 2у - 36 = 0 и уравнение его диагонали Зx + 7у - 10 = 0. Составить уравнения остальных сторон и второй диагонали этого прямоугольника.
245. Даны вершины треугольника A(1; -2), В(5; 4) и С(-2; 0), Составить уравнения биссектрис его внутреннего и внешнего углов при вершине А.
246. Составить уравнение прямой, проходящей через точку Р(3; 5) на одинаковых расстояниях от точек А(-7; 3) и B(11; -15).
247. Найти проекцию точки Р(-8; 12) на прямую, проходящею через точки А(2; -3) и В(-5; 1).
248. Найти точку M1, симметричную точке М2(8;-9) относительно прямой, проходящей через точки А (3; -4) и B(-1; -2) .
249. На оси абсцисс найти такую точку Р, чтобы сумма ее расстояний до точек М(1; 2) и N(3; 4) была наименьшей.
250. На оси ординат найти такую точку Р, чтобы разность расстояний ее до точек М(-3; 2) и N(2; 5) была наибольшей.
251. На прямой 2х - у - 5 = 0 найти такую точку Р, сумма расстояний которой до точек А (-7; 1), В(-5; 5) была бы наименьшей.
252. На прямой Зх - у - 1 = 0 найти такую точку Р, разность расстояний которой до точек A (4; 1) и B(0; 4) была бы наибольшей.
253. Определить угол φ между двумя прямыми;
1) 5х - у + 7 = 0, Зх + 2y = 0;
2) Зx - 2у + 7 = 0, 2х + 3у - 3 = 0;
3) х - 2у - 4 = 0, 2х - 4у + 3 = 0;
4) Зх + 2у - 1 = 0, 5х - 2у + 3 = 0.
255. Точка А(-4; 5) является вершиной квадрата, диагональ которого лежит на прямой 7х - у + 8 = 0. Составить уравнения сторон и второй диагонали этого квадрата.
256. Даны две противоположные вершины квадрата А(-1; 3) и С(6; 2). Составить уравнения его сторон.
257. Точка E(1; -1) является центром квадрата, одна из сторон которого лежит на -прямой х - 2у + 12 = 0. Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.
258. Из точки М0(-2; 3) под углом α к оси Ох направлен луч света. Известно, что tgα = 3. Дойдя до оби Ох, луч от нее отразился. Составить уравнения прямых, на кЪторых лежат лучи падающий и отраженный.
259. Луч света направлен по прямой x - 2y + 5 = 0. Дойдя до прямой Зх - 2y + 7 = 0, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч
260. Даны уравнения сторон треугольника Зx + 4у - 1 = 0, х - 7у - 17 = 0, 7x + y + 31 = 0. Доказать, что этот треугольник равнобедренный. Решить задачу при помощи сравнения углов треугольника,
261. Доказать, что уравнение прямой, проходящей через точку М1(х1; у1) параллельно прямой Аx + By + С = 0, может быть записано в виде A(х - x1) + B (у - y1) = 0
262. Составить уравнение прямой, проходящей через точку M1(2; -3) параллельно прямой: 1) Зх: - 7y + 3 = = 0; 2) х + 9y - 11 =0; 3) 16x - 24y - 7 = 0; 4) 2x + 3 = 0; 5) Зу - 1=0. Решить задачу, не вычисляя угловых коэффициентов данных прямых.
Указание. Воспользоваться результатом предыдущей задачи.
263. Доказать, что условие перпендикулярности пря-мых A1x + В1y + С1 = 0, A2x + В2y + С2 = 0, может быть записано в следующем виде: А1А2 + B1B2 = 0.
264. Установить, какие из следующих пар прямых перпендикулярны:
1) Зx - у + 5 = 0, x + 3y - 1 = 0;
2) Зx - 4y + 1 = 0, 4x - Зу + 7 = 0;
3) 6x - 15y + 7 = 0, 10x + 4у - 3 = 0;
4) 9x - 12y + 5 = 0, 8x - 6y - 13 = 0;
5) 7x - 2у + 1 = 0, 4х + 6y + 17 = 0;
6) 5x - 7у + 3 = 0, Зх + 2у - 5 = 0.
Решить задачу, не вычисляя угловых коэффициентов данных прямых.
Указание. Воспользоваться условием перпендикулярности прямых, выведенных в задаче 263.
265. Доказать, что формула для определения угла φ между прямыми А1x + В1у + С1 = 0, А2х + В2у + С2 = 0 может быть записана в следующем виде:
tgφ = ( A1B2 - A2B1)/(A1A2 + B1B2)
266. Определить угол φ, образованный двумя прямыми:
1) Зх - у + 5 = 0, 2х + у - 7 = 0;
2) x√2 -у√З - 5 = 0, (3 + √2)x + (√6 - √З)у+ 7 = 0;
3) x√З + у√2 - 2 = 0, x√6 - 3y + 3 = 0.
Решить-задачу, не вычисляя угловых коэффициентов данных прямых.
Указание. Воспользоваться формулой для определения угла между двумя прямыми, полученной в задаче 265.
267. Даны две вершины треугольника M1(-10; 2) и М2(6; 4); его высоты пересекаются в точке N(5; 2). Определить координаты третьей вершины М3.
268. Даны две вершины A(3; -1) и B(5; 7) треугольника AВС и точка N(4; -1). пересечения его высот. Составить уравнения сторон этого треугольника.
269. В треугольнике AВС даны: уравнение стороны АВ 5х - 3y + 2 = 0, уравнения высот AM 4х - 3y + 1=0 и BN 7х + 2у - 22 = 0. Составить уравнения двух других сторон и третьей высоты этого треугольника.
270. Составить уравнения сторон треугольника ABC, если даны одна из его вершин A(1; 3) и уравнения двух медиан х - 2y + 1 = 0 и у - 1 = 0.
271. Составить уравнения сторон треугольника, если даны одна из его вершин В(-4; -5) и уравнения двух высот 5x + Зy - 4 = 0 и Зx + 8у + 13 = 0.
272. Составить уравнения сторон треугольника, зная одну из его вершин А(4; -1) и уравнения двух биссектрис x - 1 = 0 и x - у - 1 = 0.
273. Составить уравнения сторон треугольника, зная одну его вершину B(2; 6), а также уравнения высоты х - 7y + 15 = 0 и биссектрисы 7x + y + 5 = 0, проведенных щ одной вершины.
274. Составить уравнения сторон треугольника, зная одну его. вершину B(2; -1), а также уравнения высоты 3x - 4y + 27 = 0 и биссектрисы x + 2у - 5 = 0, проведенных из различных вершин.
275. Составить уравнения сторон треугольника, зная одну его вершину С(4; -1), а также уравнения высоты 2x - Зу + 12 = 0 и медианы 2x + 3у - 0, проведенных из одной вершины.
276. Составить уравнения сторон треугольника, зная одну его вершину B(2; -7), а также уравнения высоты 3x + у + 11 = 0 и медианы а + 2у + 7 = 0, проведенных из различных вершин.
277. Составить уравнения сторон треугольника, зная одну его вершину С (4; 3), а также уравнения биссектрисы x + 2у - 5 = 0 и медианы 4x + 13y - 10 = 0, проведенных из одной вершины.
278. Составить уравнения сторон треугольника, зная одну его вершину A(3; -1), а также уравнения биссектрисы х - 4у + 10 = 0 и медианы 6x + 10y - 59 = 0, проведенных из различных вершин.
279. Составить уравнение прямой, которая проходит через начало координат и вместе с прямыми х - y + 12 = 0, 2x + у + 9 = 0 образует треугольник с площадью, равной 1,5 кв. ед.
280. Среди прямых, проходящих через точку Р(3;0), найти такую, отрезок которой, заключенный между прямыми 2x - у - 2 = 0, x + y + 3 = 0, делится в точке Р пополам.
281. Через точку Р(-3; -1) проведены всевозможные прямые. Доказать, что отрезок каждой из них, заключенный между прямыми х - 2у - 3 = 0, х - 2у + 5 = 0, делится в точке Р пополам.
282. Через точку Р(0; 1) проведены всевозможные прямые. Доказать, что среди них нет прямой, отрезок которой, заключенный между прямыми х - 2у - 3 = 0, х - 2y + 17 = 0, делился бы в точке Р пополам.
283. Составить уравнение прямой, проходящей через начало координат, зная, что длина ее отрезка, заключенного между прямыми 2х - y + 5 = 0, 2x - y + 10 = 0, равна √10.
284. Составить уравнение прямой, проходящей через точку С(-5; 4), зная что длина ее отрезка, заключенного между прямыми x + 2y + 1 = 0, х + 2у - 1 = 0, равна 5.