Эллипсоиды
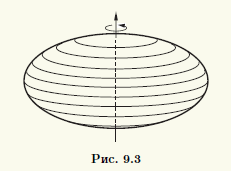
ТеорияПоверхность, которая получается при вращении эллипса вокруг одной из его осей симметрии, называют эллипсоидом вращения (рис. 9.3).
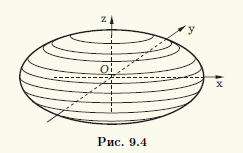
Уравнение эллипсоида вращения выведем, расположив начало прямоугольной системы ко-ординат в центре эллипса и совместив ось аппликат Oz с осью вращения, а координатную плоскость xOz — с плоскостью эллипса (рис. 9.4). Тогда уравнение эллипса будет иметь вид x2/a2 + z2/b2 = 1. Если в этом уравнении заменить x на ±√(x2 + y2) (см. 9.1), то получится уравнение (x2 + y2)/a2 + z2/b2 = 1 соответствующей поверхности вращения. Итак, эллипсоид вращения с осью вращения Oz описывается уравнением
x2/a2 + y2/a2 + z2/b2 = 1 (9.2)
Применив к эллипсоиду вращения преобразование сжатия к координатной плоскости xOz, получим эллипсоид общего вида. Если k — коэффициент сжатия, то уравнение эллипсоида будет иметь вид x2/a2 + k2y2/a2 + z2/b2 = 1, или, после переобозначения параметров,
x2/a2 + k2/b2 + z2/c2 (9.3)
Уравнение (9.3) задает поверхность второго порядка. Его называют каноническим уравнением эллипсоида. Три параметра a, b и с, входящие в него — это полуоси эллипсоида (рис. 9.5). Если все три полуоси эллипсоида попарно различны, то эллипсоид называют трехосным.
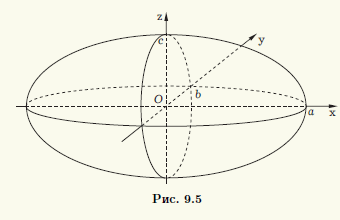
При совпадении каких-либо двух полуосей (как, например, в уравнении (9.2)) эллипсоид является поверхностью вращения (эллипсоидом вращения). Если равны все три полуоси (а = b = с = r), то эллипсоид превращается в сферу радиуса r, которая описывается уравнением х2 + у2 + z2 = r2.