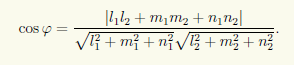Взаимное расположение прямых

Для двух прямых в пространстве возможны четыре случая:

- прямые совпадают;

- прямые параллельны (но не совпадают);

- прямые пересекаются;

- прямые скрещиваются, т.е. не имеют общих точек и непараллельны.

Рассмотрим два способа описания прямых: каноническими уравнениями и общими уравнениями. Пусть прямые L₁ и L₂ заданы каноническими уравнениями:

L₁: (x - x₁)/l₁ = (y - y₁)/m₁ = (z - z₁)/n₁, L₂: (x - x₂)/l₂ = (y - y₂)/m₂ = (z - z₂)/n₂ (6.9)

Для каждой прямой из ее канонических уравнений сразу определяем точку на ней M₁(x₁; y₁; z₁) ∈ L₁, M₂(x₂; y₂; z₂) ∈ L₂ и координаты направляющих векторов s₁ = {l₁; m₁; n₁} для L₁, s₂ = {l₂; m₂; n₂} для L₂.

Если прямые совпадают или параллельны, то их направляющие векторы s₁ и s₂ коллинеарны, что равносильно равенству отношений координат этих векторов:

l₁/l₂ = m₁/m₂ = n₁/n₂. (6.10)

Если прямые совпадают, то направляющим векторам коллинеарен и вектор M₁M₂:

(x₂ - x₁)/l₁ = (y₂ - y₁)/m₁ = (z₂ - z₁)/n₁. (6.11)

Это двойное равенство также означает, что точка М₂ принадлежит прямой L₁. Следовательно, условием совпадения прямых является выполнение равенств (6.10) и (6.11) одновременно.

Если прямые пересекаются или скрещиваются, то их направляющие векторы неколлинеарны, т.е. условие (6.10) нарушается. Пересекающиеся прямые лежат в одной плоскости и, следовательно, векторы s₁, s₂ и M₁M₂ являются компланарными. Условие компланарности этих векторов можно записать через смешанное произведение как равенство нулю определителя третьего порядка, составленного из их координат (см. 3.2):

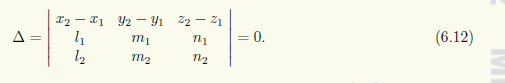
Условие (6.12) выполняется в трех случаях из четырех, поскольку при Δ ≠ 0 прямые не принадлежат одной плоскости и потому скрещиваются.

Сведем все условия воедино:

Взаимное расположение прямых характеризуется количеством решений у системы (6.13). Если прямые совпадают, то система имеет бесконечно много решений. Если прямые пересекаются, то эта система имеет единственное решение. В случае параллельных или скрещивающихся прямых решений нет. Последние два случая можно разделить, если найти направляющие векторы прямых. Для этого достаточно вычислить два векторных произведения n₁ × n₂ и n₃ × n₄, где n_i = {A_i; B_i; C_i}, i = 1, 2, 3,4. Если полученные векторы коллинеарны, то данные прямые параллельны. Иначе они скрещивающиеся.

Пример 6.4. Исследуем взаимное расположение прямых

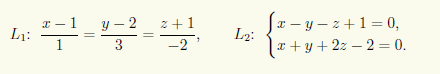
Направляющий вектор s₁ прямой L₁ находим по каноническим уравнениям этой прямой: s₁ = {1; 3; —2}. Направляющий вектор s₂ прямой L₂ вычисляем с помощью векторного произведения нормальных векторов плоскостей, пересечением которых она является:

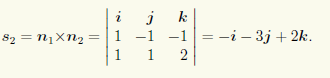
Поскольку s₁ = -s₂, то прямые параллельны или совпадают. Выясним, какая из этих ситуаций реализуется для данных прямых. Для этого подставим координаты точки M₀(1; 2; —1) ∈ L₁ в общие уравнения прямой L₂. Для первого из них получаем 1 = 0. Следовательно, точка М₀ не принадлежит прямой L₂ и рассматриваемые прямые параллельны.

Угол между прямыми. Угол между двумя прямыми можно найти, используя направляющие векторы прямых. Острый угол между прямыми равен углу между их направляющими векторами (рис. 6.5) или является дополнительным к нему, если угол между направляющими векторами тупой. Таким образом, если для прямых L₁ и L₂ известны их направляющие векторы s_x и s₂, то острый угол φ между этими прямыми определяется через скалярное произведение:

cosφ = |S₁S₂|/|S₁||S₂|

Например, пусть s_i = {l_i; m_i; n_i}, i = 1, 2. Используя формулы (2.9) и (2.14) для вычисления длины вектора и скалярного произведения в координатах, получаем