Взаимное расположение прямой и плоскости

Взаимное расположение прямой и плоскости в пространстве допускает три случая. Прямая и плоскость могут пересекаться в одной точке. Они могут быть параллельны. Наконец, прямая может лежать в плоскости. Выяснение конкретной ситуации для прямой и плоскости зависит от способа их описания.

Предположим, что плоскость π задана общим уравнением π: Ax + By + Cz + D = 0, а прямая L — каноническими уравнениями (x - x₀)/l = (y - y₀)/m = (z - z₀)/n. Уравнения прямой дают координаты точки M₀(x₀; у₀; z₀) на прямой и координаты направляющего вектора s = {l; m; n} этой прямой, а уравнение плоскости — координаты ее нормального вектора n = {A; B; C}.

Если прямая L и плоскость π пересекаются, то направляющий вектор s прямой не параллелен плоскости π. Значит, нормальный вектор n плоскости не ортогонален вектору s, т.е. их скалярное произведение не равно нулю. Через коэффициенты уравнений прямой и плоскости это условие записывается в виде неравенства A1 + Bm + Cn ≠ 0.

Если прямая и плоскость параллельны или прямая лежит в плоскости, то выполняется условие s ⊥ n, которое в координатах сводится к равенству Al + Bm + Cn = 0. Чтобы разделить случаи "параллельны" и "прямая принадлежит плоскости ", нужно проверить, принадлежит ли точка прямой данной плоскости.

Таким образом, все три случая взаимного расположения прямой и плоскости разделяются путем проверки соответствующих условий:

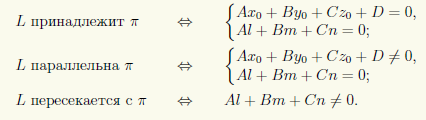
Если прямая L задана своими общими уравнениями:

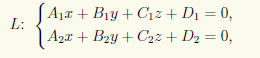
то проанализировать взаимное расположение прямой и плоскости π можно следующим образом. Из общих уравнений прямой и общего уравнения плоскости составим систему трех линейных уравнений с тремя неизвестными

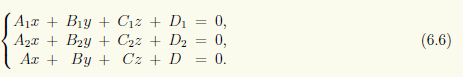
Если эта система не имеет решений, то прямая параллельна плоскости. Если она имеет единственное решение, то прямая и плоскость пересекаются в единственной точке. Последнее равносильно тому, что определитель системы (6.6)

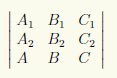
отличен от нуля. Наконец, если система (6.6) имеет бесконечно много решений, то прямая принадлежит плоскости.

Угол между прямой и плоскостью. Угол φ между прямой L: (x - x₀)/l = (y - y₀)/m = (z - z₀)/n и плоскостью π: Ax + By + Cz + D = 0 находится в пределах от 0° (в случае параллельности) до 90° (в случае перпендикулярности прямой и плоскости). Синус этого угла равен |cosψ|, где ψ — угол между направляющим вектором прямой s и нормальным вектором n плоскости (рис. 6.4). Вычислив косинус угла между двумя векторами через их координаты (см. (2.16)), получим

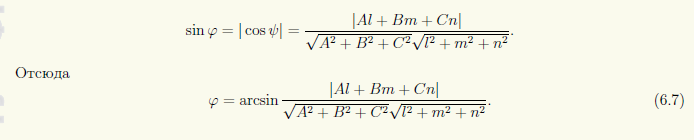
Условие перпендикулярности прямой и плоскости эквивалентно тому, что нормальный вектор плоскости и направляющий вектор прямой коллинеарны. Через координаты векторов это условие записывается в виде двойного равенства

A/l = B/m = C/n. (6.8)