Однородные системы

Следующая теорема описывает важнейшее свойство множества решений однородной системы m линейных алгебраических уравнений с n неизвестными

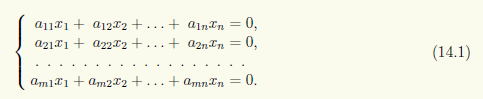
Теорема 14.1. Если столбцы x(¹), x(²), ..., x(^s) — решения однородной СЛАУ Ax = 0, то любая их линейная комбинация также является решением этой системы.

◄ Рассмотрим любую линейную комбинацию данных решений: x = Σ^s_k=1 λ_kx(^k), λ_k ∈ R. Тогда A(Σ^s_k=1 λ_kAx(^k)) = Σ^s_k=1 λ_kAx(^k) =Σ^s_k=1 λ_k0 = 0, т.е. столбец x является решением однородной СЛАУ Ax = 0. ►

Следствие 14.1. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.

◄ Если x — ненулевое решение однородной СЛАУ, то для любого λ ∈ R решением однородной СЛАУ является и λx, причем при λ₁ ≠ λ₂ решения λ₁x и λ₂x различаются. ►

Естественно попытаться найти такие решения x(¹), ... , x(^s) системы Ax = 0, чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.

Определение 14.1. Любой набор из k = n — r линейно независимых столбцов, являющихся решениями однородной СЛАУ Ax = 0, где n — количество неизвестных в системе, а r — ранг ее матрицы A, называют фундаментальной системой решений этой однородной СЛАУ.

При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице A однородной СЛАУ Ax = 0 фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.

Теорема 14.2. Пусть дана однородная СЛАУ Ax = 0 с n неизвестными и Rg A = r. Тогда существует набор из k = n—r решений x(¹), ..., x(^k) этой СЛАУ, образующих фундаментальную систему решений.

◄ Не ограничивая общности, можно считать, что базисный минор матрицы A сосредоточен в верхнем левом углу, т.е. расположен в строках 1, 2, ..., r и столбцах 1, 2, ..., r. Тогда остальные строки матрицы A, согласно теореме 12.5 о базисном миноре, являются линейными комбинациями базисных строк. Для системы Ax = 0 это означает, что если значения x₁, ... , х_n удовлетворяют уравнениям, соответствующим строкам базисного минора, т.е. первым г уравнениям, то они удовлетворяют и остальным уравнениям. Следовательно, множество решений системы не изменится, если отбросить все уравнения начиная с (r + 1)-го. Сделав это, получим систему

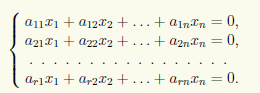
Разделим неизвестные на базисные x₁, ..., x_r и свободные x_r+1, ..., x_n, перенеся последние в правую часть, а в левой оставив базисные:

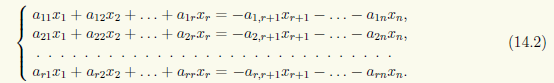
Если мы зададим произвольные значения свободных неизвестных x_r+1, ..., x_n, то относительно базисных неизвестных получим квадратную СЛАУ с невырожденной матрицей, решение которой существует и единственно. Таким образом, любое решение однородной СЛАУ однозначно определяется значениями свободных неизвестных x_r+1, ..., x_n. Рассмотрим следующие k = n — r серий значений свободных неизвестных x_r+1, ... , x_n:

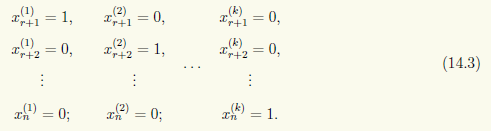
Здесь номер серии указан верхним индексом в скобках, а сами серии значений выписаны в виде столбцов. В каждой серии x⁽ⁱ⁾_r+j = 1, если j = i, и x⁽ⁱ⁾_r+j = 0, если j ≠ i.

Далее, i-й серии значений свободных неизвестных однозначно соответствуют значения x⁽ⁱ⁾₁ ,..., x⁽ⁱ⁾_r базисных неизвестных. Значения свободных и базисных неизвестных в совокупности дают решение системы (14.2). Покажем, что столбцы

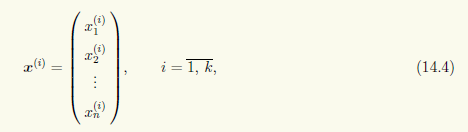
образуют фундаментальную систему решений. Так как эти столбцы по построению являются решениями однородной системы Ax = 0 и их количество равно k, то, в соответствии с определением 14.1 фундаментальной системы решений, остается доказать линейную независимость решений (14.4). Пусть есть некоторая линейная комбинация решений x(¹),..., x(^k) нулевому столбцу:

α₁x(¹) + ... + α_kx(^k) = 0.

Тогда левая часть этого равенства является столбцом, компоненты которого с номерами r + 1, ..., n равны нулю. Но (r + 1)-я компонента равна α₁1 + α₂0 +... + a_k0 = α₁. Аналогично, (r + 2)-я компонента равна α₂ и, наконец, k-я компонента равна α_k. Поэтому α₁ = α₂ = ... = α_k = 0, что означает линейную независимость решений x(¹), ..., x(^k). ►

Построенная при доказательстве теоремы 14.2 фундаментальная система решений (14.4) имеет достаточно специальный вид, поскольку, согласно (14.3), в любом из решений (14.4) все значения независимых неизвестных равны нулю, кроме одного, которое равно единице. Такие фундаментальные системы решений называют нормальными.

Следствие 14.2. С помощью нормальной фундаментальной системы решений (14.4) однородной СЛАУ (14.1) множество всех решений можно описать формулой

x = c₁x(¹) + ... + c_kx(^k), (14.5)

где постоянные c_i, i = 1,k, принимают произвольные значения.

◄ Согласно теореме 14.1, столбец (14.5) является решением рассматриваемой однородной СЛАУ Ax = 0. Поэтому остается доказать, что любое решение g = f(g₁, g₂, ..., g_n)^T этой однородной СЛАУ можно представить в виде (14.5). Рассмотрим столбец x = g_r+1x(¹) + ... + g_nx(^k). Этот столбец совпадает со столбцом g по элементам с номерами r + 1, . . . , n и является решением СЛАУ (14.2). Поэтому столбцы g и x совпадают, так как решения системы (14.2) однозначно определяются набором значений ее свободных неизвестных x_r+1, ... , x_n, а у столбцов g и x эти наборы совпадают. Следовательно, g = x = gx_r+1x(¹) + ... + g_nx(^k), т.е. решение g есть линейная комбинация столбцов x(¹), ... , x(^k) нормальной фундаментальной системы решений, что завершает доказательство. ►

Однородная СЛАУ (14.1) может иметь не только нормальные фундаментальные системы решений, но и другие фундаментальные системы решений. Оказывается, что утверждение следствия 14.2 имеет место не только для нормальной фундаментальной системы решений, но и для произвольной фундаментальной системы решений, что и утверждает следующая теорема.

Теорема 14.3. Если x(¹), ..., x(^k) — произвольная фундаментальная система решений однородной СЛАУ Ax = 0, то любое ее решение x можно представить в виде

x = c₁x(¹) + ... + c_kx(^k), (14.6)

где c₁, ... , c_k — некоторые постоянные. #

Сформулированную теорему называют теоремой о структуре общего решения однородной СЛАУ. Это вызвано тем, что, согласно теоремам 14.1 и 14.3, при заданной фундаментальной системе решений x(¹), ..., x(^k) однородной СЛАУ (14.1) выражение

x_оо = с₁x(¹) + ... + c_kx(^k), (14.7)

где с₁ , ... , c_k принимают произвольные значения, описывает все множество решений. Соотношение (14.7) называют общим решением однородной СЛАУ.